ANOVA à mesures répétées dans Excel

Ce tutoriel explique comment calculer et interpréter une Anova à mesures répétées avec Excel en utilisant XLSTAT.

Jeu de données pour ANOVA à mesures répétées

Les données ont été obtenues sur un échantillon de 24 patients en dépression séparés en deux groupes (1 : contrôle / 2 : traitement). Cinq mesures ont été effectuées sur les patients (0 : avant le début du traitement, 1 : 1 mois après le début du traitement, 3 : 3 mois après et 6 : 6 mois après). La variable dépendante représente un score permettant d’évaluer l’état de dépression du patient.

Principe de l'ANOVA à mesures répétées

Une ANOVA à mesures répétées est basée sur le même modèle qu’une ANOVA classique. L’équation du modèle est donnée par :

On a ici un facteur fixe (la variable indiquant le groupe auquel appartient chaque patient), un facteur répétition (indiquant chacune des quatre mesure faite aux différents temps) et un facteur sujet (le patient). La différence avec une analyse de la variance classique réside dans le fait que les erreurs eijk pourront être corrélées. En effet, nous ne pouvons pas supposer que les mesures sur un même sujet prises à des périodes différentes soient indépendantes.

Dans le cadre de ce tutoriel, nous utilisons la méthode des moindres carrés (LS) pour estimer notre ANOVA à mesures répétées. Dans ce cas la matrice de variance-covariance est supposée avoir une forme sphérique.

Le principe de cette méthode est simple. Une ANOVA est effectuée pour chaque mesure. Les résultats obtenus sont ceux d’une analyse de la variance classique. Ensuite des résultats supplémentaires sont donnés afin de vérifier la sphéricité de la matrice de variance-covariance des erreurs ainsi que de tester la significativité de l’impact des répétitions.

XLSTAT permet aussi d’utiliser les modèles mixtes pour traiter un modèle d’analyse de la variance à mesures répétées (voir le tutoriel suivant).

Le format des données

Les données peuvent avoir deux formats. Voir l’aide pour plus de détail. Nous nous concentrerons sur un format classique dans le cadre du modèle linéaire général. On aura donc une colonne par mesure pour la variable dépendante.

Paramétrer une ANOVA à mesures répétées

Une fois XLSTAT lancé, choisissez la commande XLSTAT / Modélisation / ANOVA à mesures répétées ou cliquez sur le bouton ANOVA à mesures répétées de la barre d'outils Modélisation.

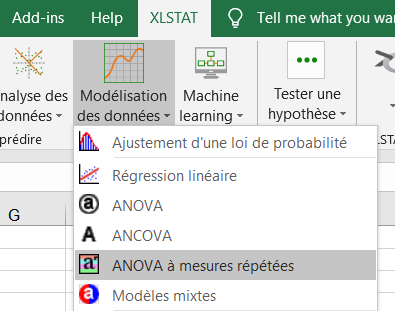
Une fois le bouton cliqué, la boîte de dialogue correspondant à l'ANOVA à mesures répétées apparaît. Dans le premier onglet, vous pouvez sélectionner les données sur la feuille Excel.

La Variable dépendante correspond à la variable expliquée (ou variable à modéliser), qui est dans ce cas précis le score réparti sur quatre colonnes (dv0-dv1-dv3-dv6).

Sélectionnez la variable group en tant que variables qualitative. L'option Libellés des colonnes est laissée activée car la première ligne des colonnes comprend le nom des variables.

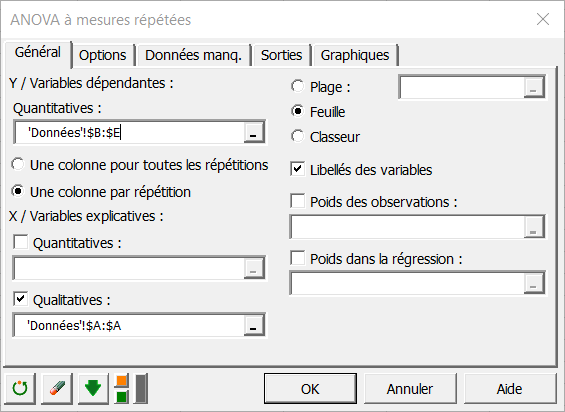
Dans l'onglet Options, nous sélectionnons comme méthode d’estimation LS (Least Squares) afin d’appliquer la méthode des moindres carrés (pour les autres méthodes voir le tutoriel sur l’ANOVA à mesures répétées basée sur les modèles mixtes ici). Nous choisissons la contrainte à a1=0, ce qui implique que le modèle s'écrira de façon à considérer que le groupe des contrôles (group=1) aura l'effet de base.

Appliquer une contrainte en ANOVA est indispensable pour des raisons théoriques, mais cela ne change ni les résultats, ni la qualité de l'analyse.

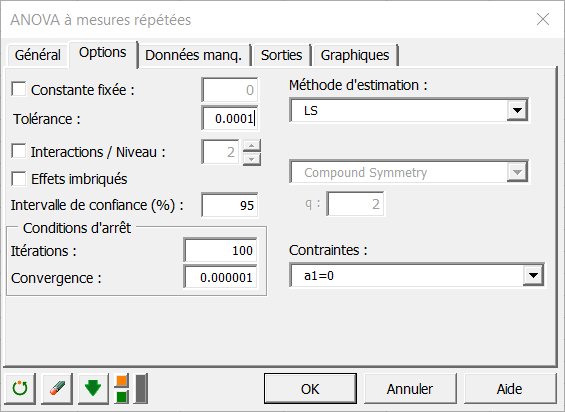
Les sorties sélectionnées sont les suivantes :

Une fois que l'utilisateur a cliqué sur OK, une nouvelle fenêtre permettant de sélectionner les facteurs fixes apparaît. La variable "répétition" doit être sélectionnée comme facteur répété et la variable "sujet" doit être sélectionnée comme facteur sujet.

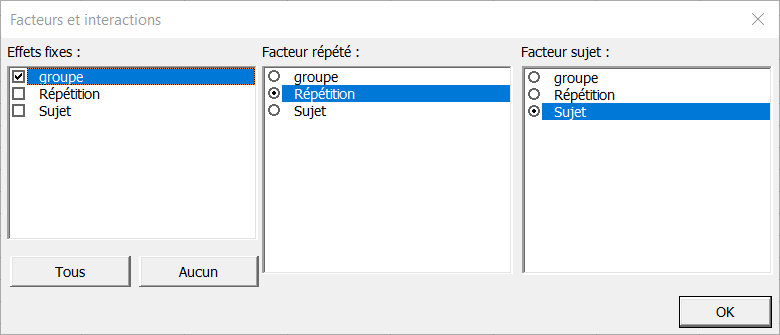
Note : XLSTAT ne permet pas de définir un facteur simultanément comme effet fixe et comme facteur sujet ou répété.

Une fois que l'utilisateur a cliqué sur OK, les calculs reprennent et les résultats sont affichés.

Interpréter les résultats de l'ANOVA à mesures répétées

Le premier tableau affiché fournit des informations sur la variable dépendante :

Tout d’abord pour chaque mesure aux temps 0, 1, 3 et 6, XLSTAT donne les résultats d’une analyse de la variance classique. Pour plus de détails sur les sorties, on peut voir le tutoriel sur l’ANOVA à un facteur ici).

Le tableau d’analyse de la variance avant le début du traitement (dv0) est :

Le tableau d’analyse de la variance 1 mois après le début du traitement (dv1) est :

Le tableau d’analyse de la variance 3 mois après le début du traitement (dv3) est :

Le tableau d’analyse de la variance 6 mois après le début du traitement (dv6) est :

Nous voyons donc que l’effet du groupe est significativement différent de 0 à partir d’un mois après le début du traitement (Pr>F plus petit que 0,05).

Une fois les quatre analyses effectuées, un test sur la matrice de covariance des erreurs est effectué. Ce test est appelé test de Mauchly.

Etant donné que la p-value est inférieure à 0,05, on doit rejeter l'hypothèse nulle que la matrice de covariance est sphérique. Afin d'ajuster cette violation, les corrections de Greenhouse-Geisser et de Huynh-Feldt ont été appliquées. Les epsilon de Greenhouse-Geisser et Huynt-Feldt sont calculés. Plus ces indices sont proches de 1, plus on s’approche d’une matrice sphérique.

Nous pouvons alors étudier les deux derniers tableaux. Tout d’abord, les effets inter-individus permettent de voir l’effet de la variable group si on ne prend pas en compte la répétition (pour toutes les répétitions simultanément). Nous voyons que le groupe a un impact significatif sur le modèle. Les effets intra-individus permettent quant à eux de voir l’impact de la mesure répétée et donc du temps : nous voyons que le temps a un impact significatif sur le score dv (facteur répétition) mais aussi que l’interaction entre la répétition et le groupe a aussi un impact significatif sur le score dv.

Ainsi, nous pouvons conclure de cette analyse que le traitement a un effet significatif sur le score des patients et que le temps a aussi un effet significatif.

Ainsi, nous avons pu étudier un modèle d’ANOVA en prenant en compte le fait que certaines observations n’étaient pas indépendantes (répétées dans le temps). D’autres sorties sont disponibles dans XLSTAT et nous permettront d’approfondir l'analyse comme, par exemple, les différents types de résidus ainsi que les graphiques associés aux résidus et aux moyennes obtenues par moindres carrés et les comparaisons multiples.