ANOVA à un facteur et tests de comparaisons multiples dans Excel
Ce tutoriel explique comment mettre en place et interpréter une ANOVA à un facteur suivie de tests de comparaisons multiples dans Excel avec XLSTAT.
Jeu de données pour la réalisation d'une ANOVA à un facteur suivie de tests de comparaisons multiples
Les données correspondent à une expérience où 4 dentifrices ont été chacun testés sur 6 personnes afin que soit mesuré leur impact sur la blancheur des dents. Tous les patients utilisaient auparavant le même dentifrice.
But de ce tutoriel sur l'ANOVA à un facteur suivie de tests de comparaisons multiples
En utilisant l'outil d'ANOVA de XLSTAT nous cherchons ici à déterminer s'il existe une différence significative entre les différents dentifrices, et si tel est le cas, quel est le dentifrice le plus efficace. Nous sommes dans un cas d'ANOVA à un facteur (le type de dentifrice) équilibrée puisque le nombre de répétitions est le même pour les différents groupes.
Paramétrer une ANOVA à un facteur suivie de tests de comparaisons multiples
-
Ouvrir XLSTAT.
-
Sélectionner la commande XLSTAT / Modélisation / Analyse de la Variance (ANOVA). Une fois le bouton cliqué, la boîte de dialogue correspondant à l'ANOVA apparaît.
-
Sélectionner les données sur la feuille Excel. La Variable dépendante correspond à la variable expliquée, soit dans ce cas précis, à la "blancheur" des dents dont nous voulons expliquer la variabilité par la variable explicative qualitative "Dentifrice".
-
Activer l'option Libellés des variables car la première ligne des colonnes comprend le nom des variables.
Dans XLSTAT, il est possible de sélectionner les données de deux façons différentes pour l’ANOVA. La première est sous forme de colonne, une colonne pour la variable dépendante, une autre pour la variable explicative.
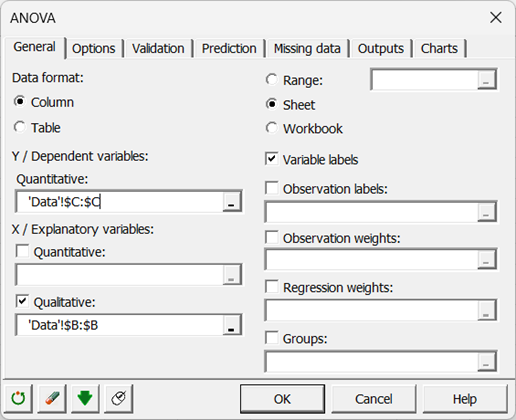
La seconde manière de sélectionner les données est sous forme de tableau, avec chaque colonne représentant une modalité de la variable explicative.
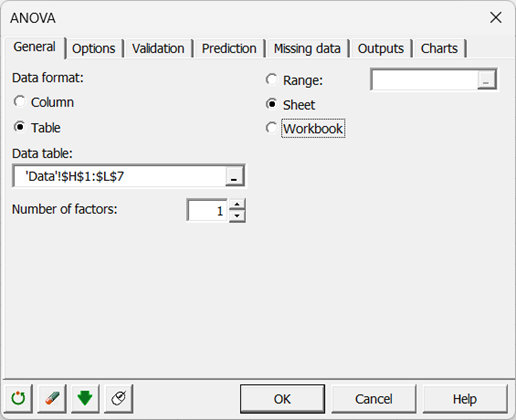
-
Dans l'onglet Options, choisir la contrainte à a1=0. Cela signifie que nous voulons construire le modèle en partant de l'hypothèse que le dentifrice T1 a l'effet de base sur la blancheur : nous savons que la moyenne pour T1 est la plus basse et cela garantit que les autres effets seront positifs.
-
L'application d'une contrainte au modèle ANOVA est indispensable pour des raisons théoriques, mais cela ne change ni les résultats (prévisions, R², etc.), ni la qualité de l'analyse.
-
Dans l'onglet Sorties / Moyennes, cocher le test de Tukey et REGWQ dans le champ Comparaison par paires puis cocher le test bilatéral de Dunnett dans l'option Comparaisons avec un contrôle.
-
Dans la boîte de dialogue de sélection de la catégorie de contrôle, choisir le groupe de contrôle T1 pour le test de Dunnett.
-
Cliquez sur OK pour lancer les calculs.
Interpréter les résultats d'une ANOVA à un facteur suivie de tests de comparaisons multiples
Le premier tableau de résultats fournit les coefficients d'ajustement. Le R² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, expliqué par les variables explicatives. Plus ce coefficient est proche de 1, meilleur est le modèle. Dans notre cas, 56% de la variabilité est expliquée par le type de dentifrice. Le reste de la variabilité est explicable par des effets qui ne sont ni recensés, ni mesurés dans cette analyse.
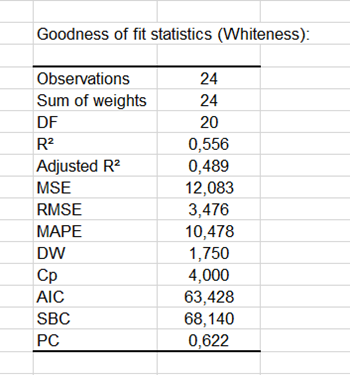
Le tableau d'analyse de la variance est un résultat qui doit être analysé attentivement (voir ci-dessous). C'est à ce niveau que l'on teste si l'on peut considérer que la variable explicative sélectionnée (le type de dentifrice) apporte une quantité d'information significative au modèle (hypothèse nulle H0) ou non. En d'autres termes, c'est un moyen de tester si la moyenne de la variable à modéliser suffit à décrire les résultats obtenus ou non.
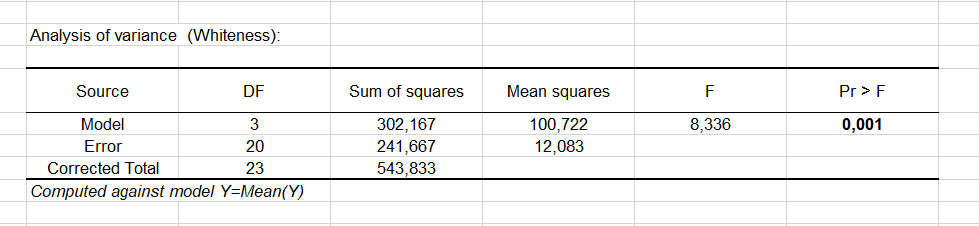
Le test du F de Fisher est utilisé. Étant donné que la probabilité associée au F est dans ce cas de 0.001, cela signifie que l'on prend un risque de 0.1% en concluant que la variable explicative apporte une quantité d'information significative au modèle.
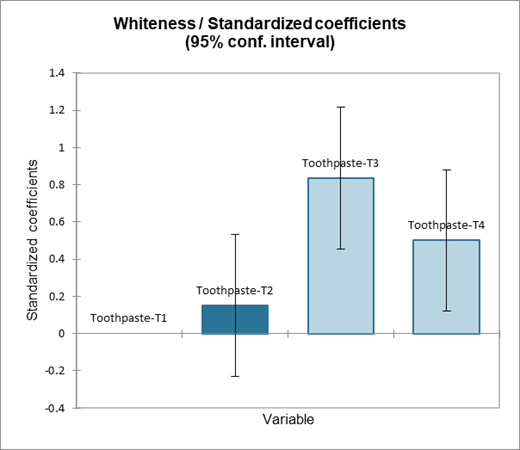
Le tableau suivant fourni les détails sur le modèle et est essentiel dès lors que le modèle doit être utilisé pour effectuer des prévisions ou des simulations. Dans notre cas particulier il a peu d'intérêt. On remarquera simplement que l'intervalle de confiance pour l'effet du dentifrice T2 comprend la valeur 0, ce qui indique que le dentifrice T2 n'est pas significativement différent de T1.
Le diagramme en bâtons des coefficients standardisés permet de comparer visuellement les impacts relatifs des modalités, et de voir quels intervalles de confiance comprennent la valeur 0.
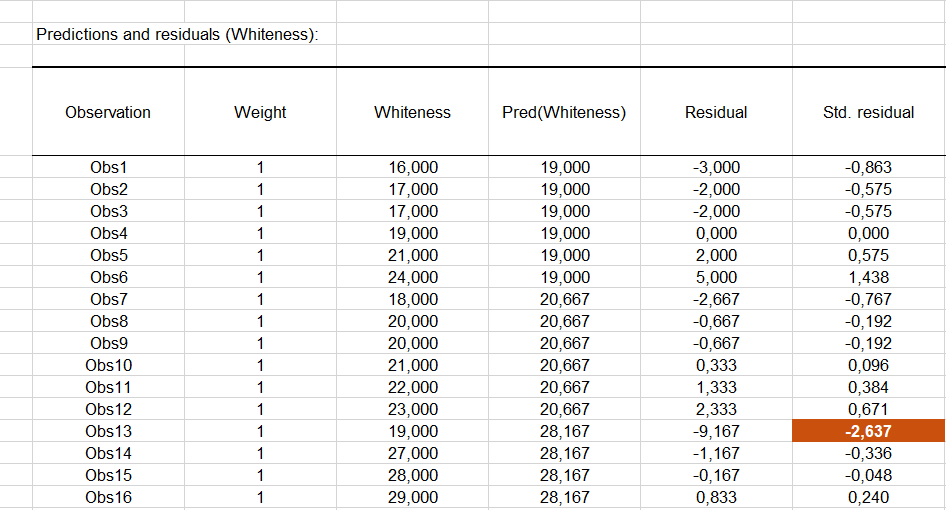
Le tableau suivant présente l'analyse des résidus. Une attention particulière doit être portée aux résidus centrés réduits, qui, étant donné les hypothèses liées à l'ANOVA, doivent être distribués suivant une loi normale N(0,1). Cela signifie, entre autres, que 95% des résidus doivent se trouver dans l'intervalle [-1.96, 1.96]. Étant donné le faible nombre de données dont on dispose ici, toute valeur en dehors de cet intervalle est révélatrice d'une donnée suspecte. Nous pouvons ici identifier une valeur suspecte (13ième observation) le résidu étant égal à -9.17. Afin d'expliquer cette valeur, on pourra vérifier que le bon dentifrice a bien été donné à la personne en question, ou analyser la raison pour laquelle la réaction du patient au dentifrice a été plus faible que pour les autres.
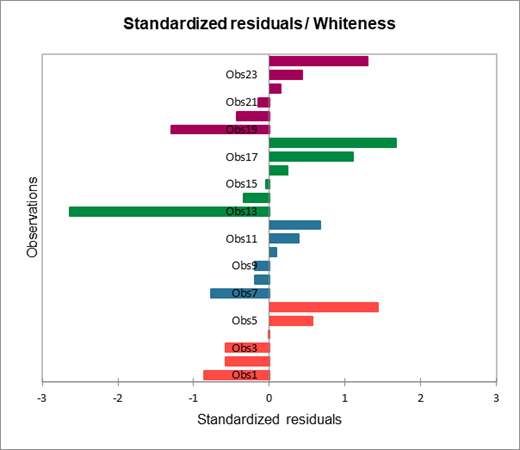
L'histogramme des résidus centrés réduits permet de repérer rapidement la présence de valeurs hors de l'intervalle [-1.96, 1.96].
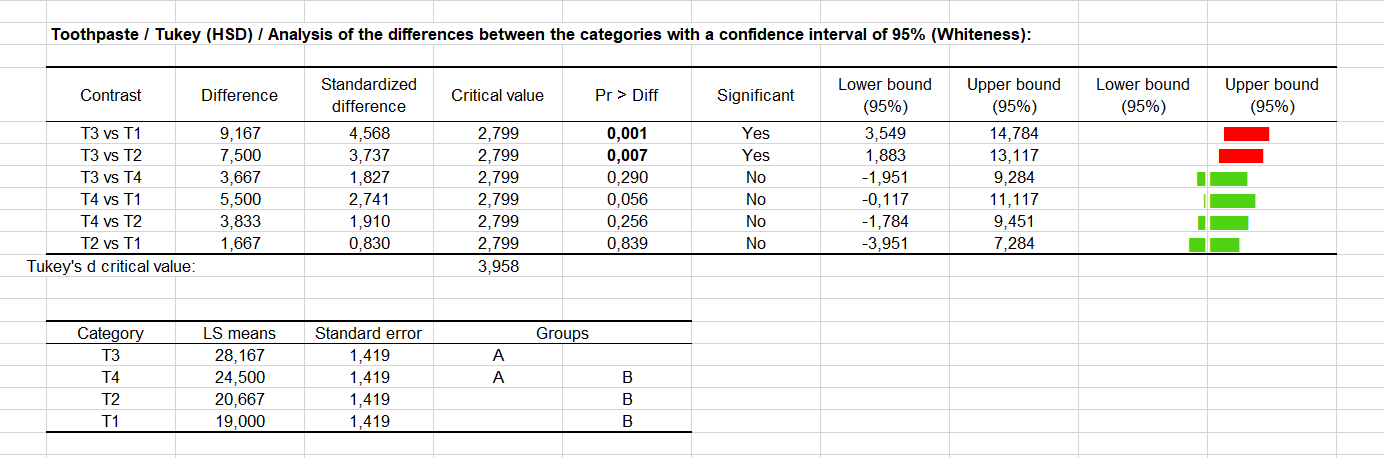
Enfin, nous allons pouvoir répondre à notre question initiale: y a-t-il une différence significative entre les dentifrices, et si oui, comment peut-on les classer. Comme il est montré dans le tableau ci-dessous, le test de Tukey HSD (Honestly Significantly Different), a été appliqué à l'ensemble des couples de différences possibles. Le risque de 5% que nous avons choisi est utilisé pour déterminer la valeur critique q, qui est comparée à la différence standardisée entre les moyennes. D'autres logiciels se basent sur la valeur "d" aussi fournie par XLSTAT. Seulement deux paires semblent être significativement différentes (T1, T3) et (T2,T3). Les intervalles de confiance le confirment également. Si l'intervalle ne contient pas la valeur zéro alors nous pouvons rejeter l'hypothèse nulle qu'il n'y a pas de différence significative entre deux dentifrices.
La procédure REQWQ donne un résultat différent (voir ci-dessous), ce qui montre que l'on doit être prudent lorsque l'on utilise des procédures de comparaisons multiples. Trois couples de modalités sont ici significativement différentes: contrairement à ce qui était le cas ci-dessus, T1 et T4 sont ici jugés comme étant significativement différents. Le tableau des regroupements fait donc ressortir trois groupes de modalités.
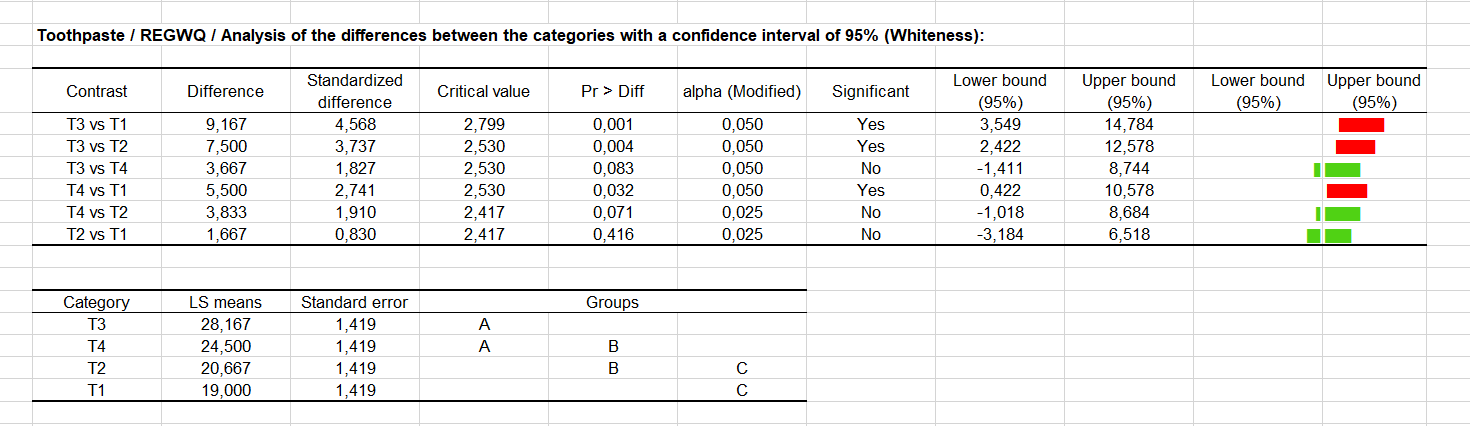
Le test de Dunnett a été calculé pour comparer chaque modalité avec la modalité T1. Le test de Dunnett fait aussi ressortir une différence significative entre T1 et T4.
Conclusion pour cette ANOVA à un facteur
En conclusion, les différentes pâtes de dentifrice testées ont un impact significativement différent sur la blancheur des dents. Comme le dentifrice T1 est déjà sur le marché, afin de promouvoir le nouveau produit, les dentifrices T3 ou T4 pourront être sélectionnés pour être mis sur le marché.
Cet article vous a t-il été utile ?
- Oui
- Non

