One-Way ANOVA & Mehrfachvergleiche in Excel

Dieses Tutorium wird Ihnen helfen, eine ANOVA (Analysis of Variance) mit einem Faktor gefolgt von Tukey & Dunnetts vielfachen Vergleichen in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.

Datensatz für die Durchführung einer ANOVA mit einem Faktor

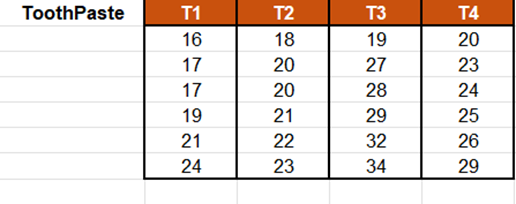
Die Daten entsprechen einem Experiment, bei dem 4 neue Formulierungen einer Zahnpasta an jeweils 6 verschiedenen Patienten getestet werden, um den Effekt auf die Zahnweisse zu messen.

Absicht dieses Tutoriums

Durch den Einsatz der ANOVA-Funktion von XLSTAT soll überprüft werden, ob die Ergebnisse je nach verwendeter Formulierung unterschiedlich sind. Ist dies der Fall, so soll die effektivste Formulierung zu finden. Der vorliegende Fall ist eine einfache balanzierte ANOVA, da es nur einen Faktor gibt - die Formulierung - und die Anzahl der Wiederholungen die gleich für jede der Formulierungen ist.

Einrichten einer ANOVA mit einem Faktor

• Öffnen Sie XLSTAT.

• Wählen Sie den Befehl XLSTAT / Datenmodellierung / ANOVA. Sobald Sie auf die Schaltfläche geklickt haben, erscheint das ANOVA-Dialogfeld.

• Wählen Sie die Daten im Excel-Blatt aus. Die abhängige Variable entspricht hier der "Weißheit", deren Variabilität wir durch den Einfluss der "Zahnpasta"-Formel erklären möchten, wobei letztere die qualitative erklärende Variable ist.

• Stellen Sie sicher, dass Sie die Option Variablenbezeichnungen aktivieren.

In diesem Beispiel möchten wir die Ergebnisse auf dem gleichen Blatt anzeigen, auf dem die Daten gespeichert sind, daher haben wir die Option Bereich gewählt und die Zelle ausgewählt, die der oberen linken Ecke des Ergebnisberichts entspricht, der angezeigt werden soll.

In XLSTAT ist es möglich, die Daten auf zwei verschiedene Arten für die ANOVA auszuwählen. Die erste besteht in der Form von Spalten, eine Spalte für die abhängige Variable und eine weitere für die erklärende Variable.

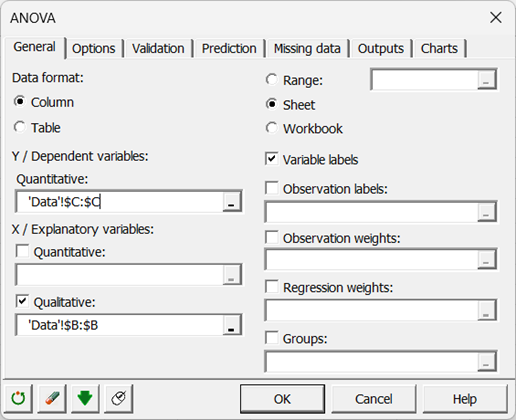
Die zweite Möglichkeit, die Daten auszuwählen, ist in tabellarischer Form, wobei jede Spalte eine Modalität der erklärenden Variablen darstellt.

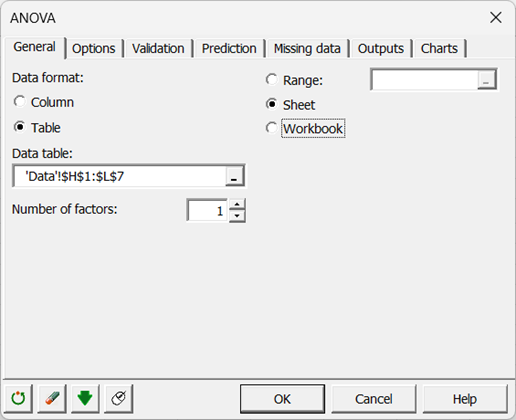
• Im Options-Tab lassen Sie die Einschränkungsoption bei a1=0. Dies bedeutet, dass das Modell unter der Annahme erstellt wird, dass die Zahnpasta T1 den grundlegenden Effekt auf die Weißheit hat: Wir wissen, dass der Durchschnitt für T1 am niedrigsten ist und dies garantiert, dass die anderen Effekte positiv sein werden.

• Das Anwenden einer Einschränkung auf das ANOVA-Modell ist aus theoretischen Gründen notwendig, hat jedoch keinen Einfluss auf die Ergebnisse (Güte der Anpassung, Vorhersagen). Der einzige Unterschied besteht darin, wie das Modell geschrieben wird.

• Im Outputs-Tab (Untertab "Mittelwerte“) wählen Sie einen Tukey-Test und einen REGWQ-Test im Feld "Paarweise Vergleiche“ aus.

• Aktivieren Sie die Option "Vergleiche mit einer Kontrolle“, um einen zweiseitigen Dunnett-Test durchzuführen.

• Klicken Sie auf OK, um die Berechnungen zu starten.

• Im Auswahl-Dialogfeld der Kontrollkategorie wählen Sie die T1-Kontrollgruppe für den Dunnett-Test aus.

• Nachdem Sie auf die OK-Schaltfläche geklickt haben, werden die Berechnungen fortgesetzt und die Ergebnisse angezeigt.

Interpretieren der Ergebnisse einer ANOVA mit einem Faktor

Die erste Tabelle zeigt die Koeffizienten der Anpassungsgüte des Modells an. Das R(Korrelationskoeffizient), R² (Determinationskoeffizient) und das angepasste R².

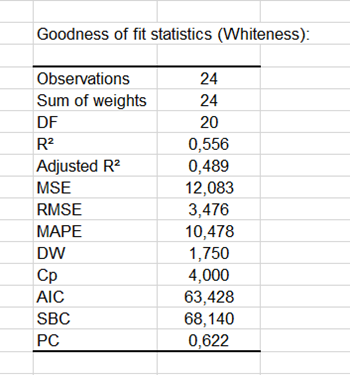
Der Determinationskoeffizient (hier 0.56) gibt den Prozentsatz der Variabilität der abhängigen Variablen (hier die Zahnweisse) an, die durch die erklärende Variable beschrieben (hier der Zahnpastatyp) wird. In unserem Fall wird 56% der Variabilität erklärt. Die übrigen 44% sind in anderen Variablen versteckt, die nicht verfügbar sind und die das Modell in den "Zufallseffekten" verbirgt. Es ist wichtig die Ergebnisse der Varianzanalyse-Tabelle zu untersuchen (siehe unten). Diese Ergebnisse lassen uns entscheiden, ob die erklärenden Variablen eine signifikante Information (Nullhypothese H0) in das Modell einbringen oder nicht. Mit anderen Worten ausgedrückt, ist dies eine Art zu überprüfen, ob es Sinn macht den Mittelwert zu benutzen, um die gesamte Population zu beschreiben, oder ob die Information, die von der/den erklärenden Variable(n) eingebracht wurde, wertvoll ist.

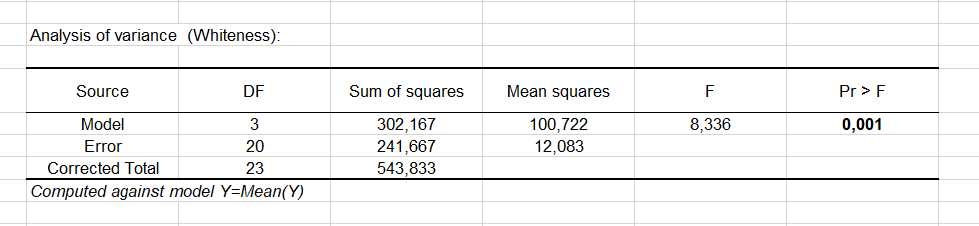
Fisher's F Test wird eingesetzt. Anhand der Tatsache, dass die Wahrscheinlichkeit die dem F value entspricht kleiner als 0.001 ist, ist das Risiko kleiner als 0.01%, dass die Annahme der Nullhypothese (kein Einfluss der erklärenden Variable der Zahnpastaformulierung) falsch ist. Daher kann man sicher schließen, dass ein Effekt der Zahnpastaformulierung auf die Zahnweisse besteht. Berücksichtigen Sie, dass der R² nicht sehr gut (0.56) ist, was besagt, dass ein Teil der Information für eine zusätzliche Erklärung der Variation der Zahnweisse fehlt. Dies ist nicht sehr überraschend.

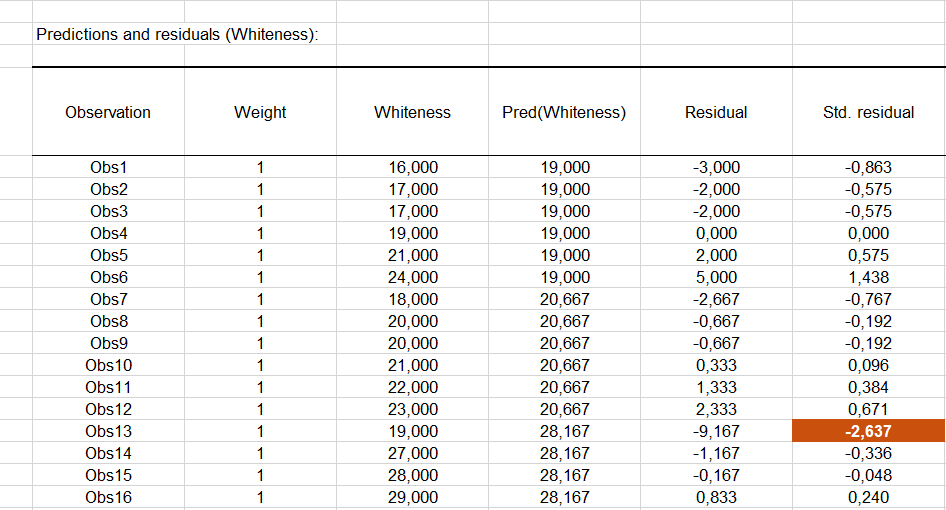
Die folgende Tabelle stellt die Einzelheiten des Modells dar. Diese Tabelle ist nützlich, falls Vorhersagen benötigt werden. In diesem Fall ist sie nicht sehr nützlich. Man kann schon feststellen, dass Zahnpasta T2 einen Effekt aufweist, dessen 95% Konfidenzintervall die 0 einschießt, was darauf deutet, dass es nicht offensichtlich ist, dass T2 sehr verschieden von T1 ist.

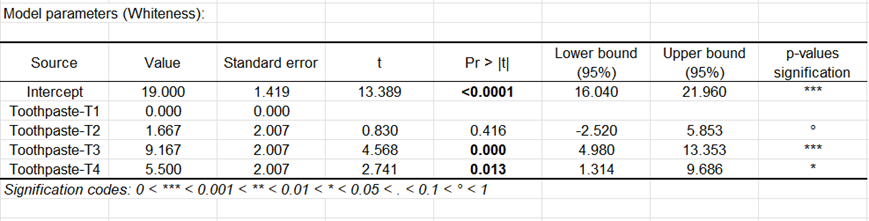
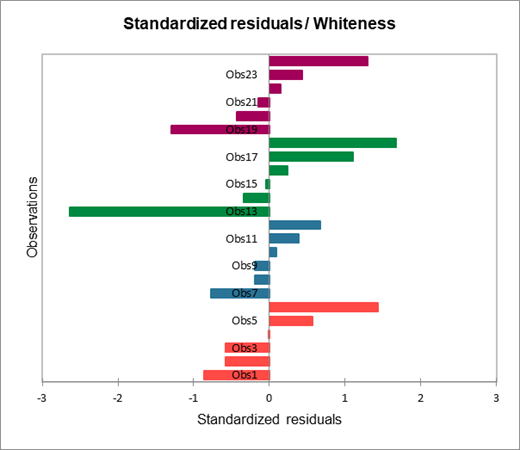
Das Balkendiagramm der standardisierten Koeffizienten erlaubt es, visuell den relativen Einfluss der Modalitäten zu vergleichen und zu sehen, ob das Konfidenzintervall die 0 einschließt oder nicht.

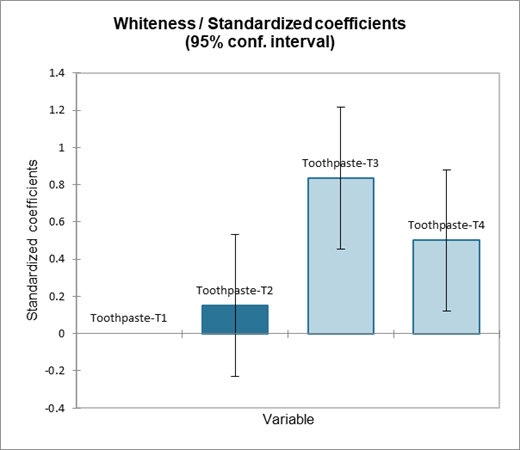
Die nächste Tabelle zeigt die Residuen an. Man kann die reduzierten Residuen (standardisierte Residuen) genauer betrachten, die nach den Prämissen der ANOVA normalverteilt sein sollten. Dies bedeutet unter anderem, dass 95% der Residuen im Intervall [-1.96, 1.96] liegen. Alle Werte außerhalb dieses Intervalls sind potentielle Ausreißer oder deuten darauf, dass die Normalitätsannahme falsch ist. Es scheint hier einen starken Ausreißer vorzuliegen (13te Beobachtungen) mit einem Residuum von -2.8279. Um die Differenz zu erklären, sollte zunächst überprüft werden, ob dem 13ten Patienten die richtige Zahnpasta gegeben wurde und zweitens sollte man zu verstehen suchen, warum die Antwort auf die Formulierung nicht die gleiche war wie für andere Patienten. Das Histogramm der Residuen erlaubt es rasch die Residuen zu sehen, die außerhalb des erwarteten Bereiches liegen.

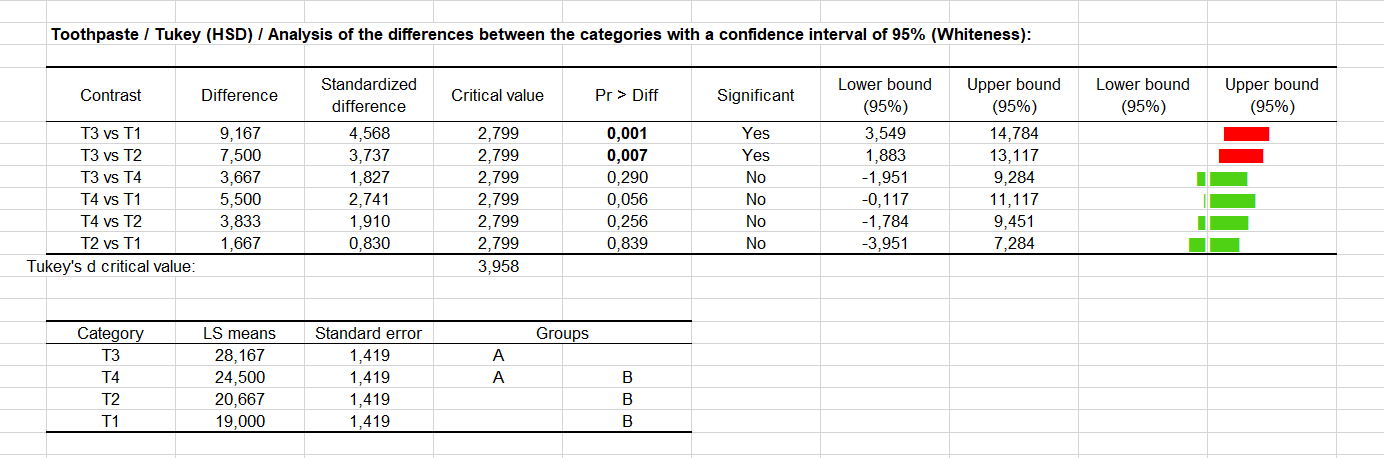
Nun erhalten wir Antwort auf unsere Ausgangsfrage: Besteht ein signifikanter Unterschied zwischen den Behandlungen und wie sollte dieser Unterschied klassifiziert werden? Wie in der nächsten Tabelle angezeigt, wird der Tukey HSD Test (Honestly Significantly Different) auf alle paarweisen Differenzen zwischen den Mittelwerten angewendet. Das ausgewählte 5% Risiko wird benutzt, um den kritischen Wert q zu erhalten, der mit den standardisierten Differenzen zwischen den Mittelwerten verglichen wird. Andere Softwarepakete geben den d Wert als Ergebnis, wie XLSTAT. Nur zwei Paare scheinen signifikant verschieden zu sein (T1, T3) und (T2,T3). Die Mittelwerte und die Modalitäten werden dann auf Basis dieser Analyse klassifiziert. Man kann erkennen, das es keine Transitivität gibt (> bezeichnet nicht signifikant verschieden, und <> bezeichnet signifikant verschieden): T4 > T3 T4 > T2 aber T2 <> T3

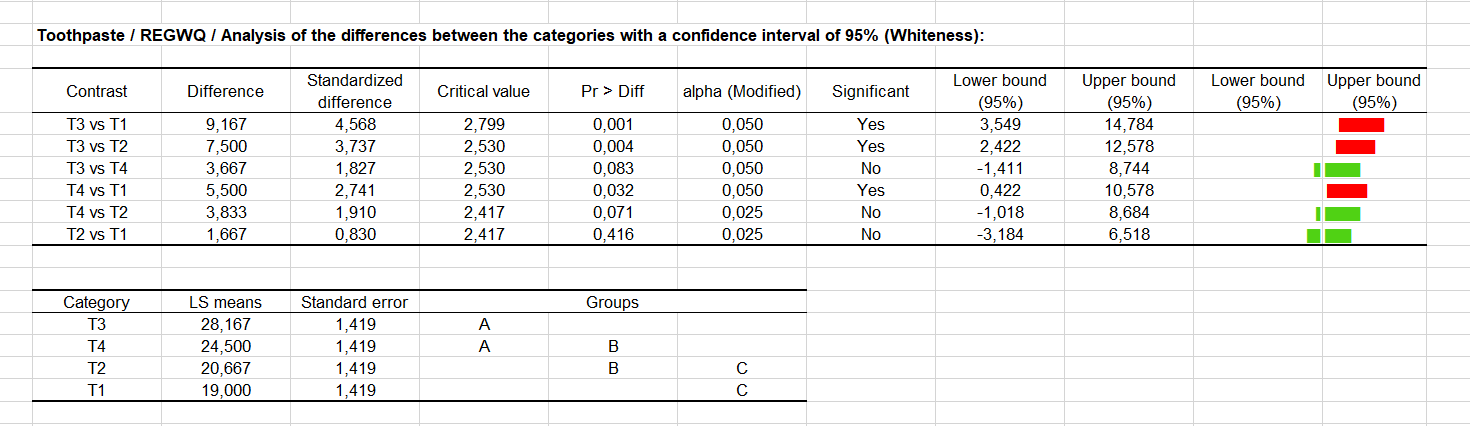
Das REQWQ Verfahren führt zu unterschiedlichen Ergebnissen (siehe unten), was darauf hinweist, dass man bei dem Gebrauch von multiplen Vergleichsmethoden vorsichtig sein muss. In diesem Fall sind drei Paare von Modalitäten verschieden (T1 und T4 scheinen signifikant verschieden nach dieser Methode). Die Gruppierung gibt nun drei übergreifende Gruppen von Modalitäten.

Im Anschluss wurde ein Dunnett Test durchgeführt, um jede Modalität mit der Kontrollkategorie T1 zu vergleichen. Dunnett Test stimmt mit dem Verfahren REQWQ darin überein, dass die Modalitäten T1 und T4 signifikant verschiedenen sind.

Schlussfolgerung für diese ANOVA mit einem Faktor

Man kann schließen, dass die 4 Zahnpastaformulierungen signifikante Effekte auf die Zahnweisse haben. Da die Zahnpaste T1 schon auf dem Markt ist, sollten die Zahnpasta T3 oder T4 gewählt werden, da sie einen signifikanten Anstieg der Zahnweisse aufweisen, als einen Kandidaten zur Markteinführung.

Bitte beachten Sie, dass eine ANOVA auf parametrischen Annahmen basiert, die überprüft werden müssen, um die Zuverlässigkeit der Ausgabe sicherzustellen.