Mischmodelle mit zufälligen Komponenten in Excel

Dieses Tutorium wird Ihnen helfen, ein gemischtes Modell mit zufälligen Komponenten in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.

Datensatz für die Durchführung eines gemischten Modells mit zufälligen Komponenten

Die Daten stammen aus Mendenhall, Wackerly and Schaeffer (1996, Mathematical Statistics with Applications, Duxbury Press). In diesem Beispiel, werden Barren verschiedener Metalle untersucht. Man sucht den Einfluss der Barrenbehandlung und des verwendeten Metall als Legierung in diesem Barren (N = Nickel, I = Eisen und C = Kupfer) auf den notwendigen Druck um den Barren in zwei zu brechen. Es liegen 7 Barren, drei Legierungen und eine abhängige Variable vor. Die behandelten Barren wurden aus einer größeren Population gezogen und stellen daher einen zufälligen Faktor in unserem Modell dar.

Ein gemischtes lineares Modell basiert auf dem gleichen Modell wie ein herkömmliches lineares Modell mit einem Term, der dem zufälligen Effekt zugeordnet wird. Das Modell hat die folgende Form:

In unserem Fall ist Y die Druckvariable, X die Legierung (fixer Faktor) und Z ist der Barren (zufälliger Faktor). Weiterhin kann die Kovarianzstruktur der Matrix der zufälligen Effekte gewählt werden. Es wird die Struktur der „Varianzkomponenten“ gewählt, die auf einer Diagonalmatrix basiert. Bitte lesen Sie in der XLSTAT-Hilfe nach, um mehr Einzelheiten über die Kovarianzstrukturen zu erfahren.

Einrichten eines gemischten Modells mit zufälligen Komponenten

• Nach dem Start von XLSTAT wählen Sie den XLSTAT/Modellierung der Daten/Gemischte Modelle Befehl oder klicken Sie auf den zugehörigen Button in der "Modellierung der Daten" Toolbar (siehe unten).

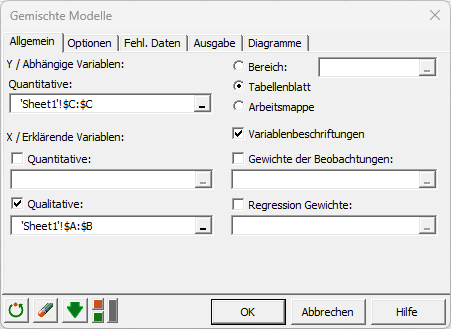
• Nach dem Klicken des Buttons, erscheint das Dialogfenster. Wählen Sie nun die Daten, die den zu berücksichtigenden Variablen entsprechen auf dem Excel-Blatt aus. Die „abhängige Variable“ (oder zu modellierende Variable) ist hier die Spalte „Druck“.

• Unser Ziel ist es den Effekt der Legierung, und des Barren auf die Variabilität des Drucks zu bestimmen.

• Da die Spaltennamen für die Variablen ausgewählt wurden, aktivieren Sie bitte die Option „Beschriftung der Variablen“.

• Wählen Sie anschließend die wiederholten und Subjektfaktoren als erklärende Variablen.

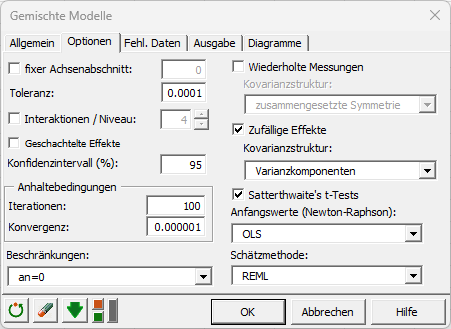
• Im Reiter Optionen, lassen Sie die Beschränkungsoption bei "an=0", was bedeutet, dass ein Modell mit der letzte Modalität der Variablen Legierung (hier „Kupfer“) als Standardeffekt für den Druck erstellt wird.

• Obwohl Sie aus theoretischen Gründen eine Beschränkung anwenden müssen, hat diese keine Auswirkung auf die Ergebnisse (wie die Anpassungsgüte) des Modells.

• Der einzige Unterschied liegt in der Modellschreibweise.

• Die Kovarianzstruktur wird als Vorgabewert der Varianzkomponenten gewählt.

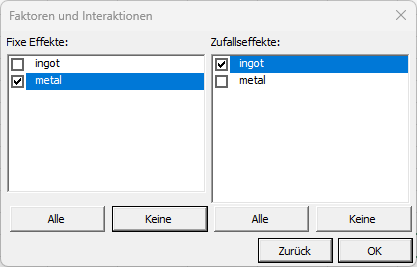
• Nach dem Klicken auf den OK Button, wird ein Dialogfenster zur Auswahl der Faktoren die im Modell zu berücksichtigen sind angezeigt. Der fixe Effekt ist das Metall und der zufällige Effekt ist die Legierung.

• Bemerkung: Ein Faktor kann nicht zufällig und fix gleichzeitig sein.

• Nach dem Klicken auf den OK Button, beginnen die Berechnungen und die Ergebnisse werden auf einem neuen Excel-Blatt angezeigt.

Interpretieren der Ergebnisse eines gemischten Modells mit zufälligen Komponenten

Die erste Tabelle zeigt die Koeffizienten der Anpassungsgüte des Modells an.

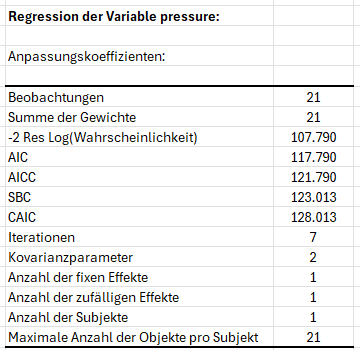
Die Modellparameter werden mittels der beschränkten Methode der maximalen Wahrscheinlichkeit (REML) ermittelt und sind unterschiedlich im Vergleich zu einer klassischen ANOVA. Alle Indizes werden benutzt, um Modelle mit verschiedener Kovarianzstruktur zu vergleichen.

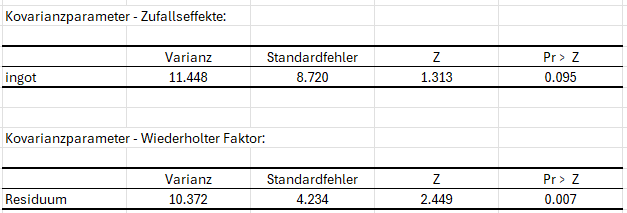
Anschließend werden die Kovarianzparametertabellen angezeigt. Die erste Tabelle ist den Parametern der zufälligen Komponenten des Modells zugeordnet und die zweite Tabelle ist den Kovarianzmatrix der Fehler zugeordnet. Da in unserem Fall keine wiederholten Messungen vorliegen, ist die Kovarianzmatrix der Fehler eine Diagonalmatrix mit einem Wert, der der Varianz entspricht. Die gesamte Kovarianzmatrix wird angezeigt, falls die G Matrix (Kovarianz zufälliger Komponenten) und die R Matrix (Fehlerkovarianz) im Reiter „Ausgabe“ des Dialogfensters aktiviert wurden. Man kann sehen, dass die Fehlervarianz signifikant ist und dass die Varianz der zufälligen Komponente nicht signifikant ist. Die zufällige Komponente wird daher keinen signifikanten Effekt auf das globale Modell haben.

Um den Einfluss der fixen Effekte auf das Modell zu verstehen, werden die Typ III Tests der fixen Effekte untersucht. Man kann feststellen, dass das Metall einen signifikanten Einfluss auf das Modell hat.

Das verwendete Metall hat einen signifikanten Einfluss auf den notwendigen Druck, um den Barren zu zerbrechen.

Betrachtet man die Modellparameter (siehe unten), so kann man feststellen, dass Eisen als Legierung den signifikantesten Anstieg auf den notwendigen Druck bewirkt. Die Verwendung von Nickel führt zu einem signifikanten Unterschied.

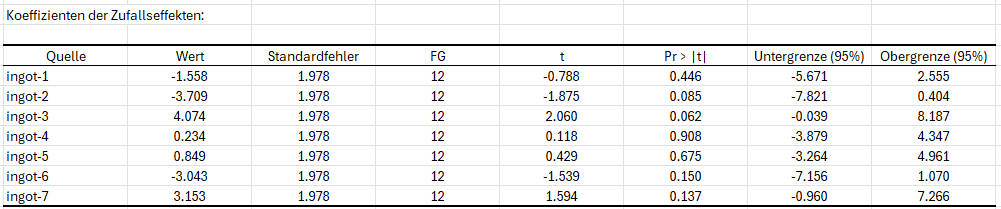
Betrachtet man die Koeffizienten der zufälligen Effekte, so kann man sehen, dass Koeffizienten nicht signifikant sind und daher schießen, dass die Behandlung des Barrens keinen Einfluss auf das Modell hat.

Zusammenfassend kann man sagen, dass die Legierung der einzige Faktor des Modells ist, der einen signifikanten Einfluss auf den notwendigen Druck zum Zerbrechen des Barrens hat. Weitere nützliche Ergebnisse sind in XLSTAT verfügbar, wie unter anderem die Residuen, die Residualdiagramme, die Diagramme der Quadratmittelwerte.