ANOVA à mesures répétées sur des données incomplètes en utilisant les modèles mixtes
Ce tutoriel explique comment mettre en place et interpréter une analyse de variance à mesures répétées grâce aux modèles mixtes lorsque les données sont déséquilibrées avec Excel en utilisant XLSTAT.
Jeu de données
Les données correspondent à l’évaluation d’un score de dépression mesuré à différents temps chez 24 patients séparés en deux groupes : un groupe ayant subi un traitement et un groupe de contrôle n’ayant pas subi de traitement.
Nous disposons des 4 variables suivantes :
- Sujet : Cette variable qualitative contient l’identifiant du patient.
- Groupe : Cette variable qualitative permet de connaitre le groupe auquel appartient le patient (1 : contrôle / 2 : traitement).
- Temps : Cette variable qualitative indique à quel moment la mesure du score a été effectuée, elle comporte 5 modalités (0 : avant le début du traitement, 1 : 1 mois après le début du traitement, 3 : 3 mois après et 6 : 6 mois après).
- dv : La variable dépendante quantitative représente un score permettant d’évaluer l’état de dépression du patient.
Les données sont déséquilibrées c’est à dire que les effectifs de toutes les modalités d’au moins un des facteurs ne sont pas égaux. Par exemple, on voit ici que le sujet 1 n’a pas été mesuré au temps 6 alors que le sujet 2 oui.
Une ANOVA à mesures répétées est basée sur le même modèle qu’une ANOVA classique, dans notre cas, l’équation du modèle s’écrira :
![]() On aura donc deux facteurs fixes (les variables « groupe » et « temps ») et un facteur d’interaction (« groupe * temps »). La différence avec une analyse de la variance classique réside dans le fait que les erreurs eijk pourront être corrélées. En effet, nous ne pouvons pas supposer que les mesures sur un même sujet prises à des périodes différentes soient indépendantes.
On aura donc deux facteurs fixes (les variables « groupe » et « temps ») et un facteur d’interaction (« groupe * temps »). La différence avec une analyse de la variance classique réside dans le fait que les erreurs eijk pourront être corrélées. En effet, nous ne pouvons pas supposer que les mesures sur un même sujet prises à des périodes différentes soient indépendantes.
Dans le cadre des modèles mixtes, l’équation du modèle s’exprime sous la forme suivante :
![]() où Y est la variable quantitative à expliquer, X rassemble les facteurs associés aux effets fixes (ce sont les variables classiques de la régression linéaire), β est un vecteur de coefficients associés aux effets fixes, Z est une matrice rassemblant les effets aléatoires (ce sont des variables qui ne peuvent pas être supposées fixes), γ est un vecteur de coefficients associés aux effets aléatoire et ε est un vecteur rassemblant les erreurs associées à chaque observation.
où Y est la variable quantitative à expliquer, X rassemble les facteurs associés aux effets fixes (ce sont les variables classiques de la régression linéaire), β est un vecteur de coefficients associés aux effets fixes, Z est une matrice rassemblant les effets aléatoires (ce sont des variables qui ne peuvent pas être supposées fixes), γ est un vecteur de coefficients associés aux effets aléatoire et ε est un vecteur rassemblant les erreurs associées à chaque observation.
Afin de reproduire une anova à mesures répétées avec les modèles mixtes, une solution est d’inclure le facteur sujet en tant que variable aléatoire du modèle mixte (avec une structure de covariance type « composante de la variance ») et de déclarer une structure d’erreur résiduelle du même type.
Pour les modèles mixtes comportant des structures de covariance complexes et / ou des ensembles de données non équilibrés comme dans le cas présent, les statistiques de test pour les effets fixes suivent des distributions inconnues et non plus des test F (Fisher) exact. En supposant que les statistiques de test suivent approximativement une distribution F, XLSTAT implémente une approximation des erreurs du modèle (Satterthwaite -1946) en trouvant la combinaison linéaire appropriée des sources de variation aléatoires du terme d'erreur pour tester la signification de chaque effet fixe du modèle en question.
Paramétrer une ANOVA à mesures répétées avec les modèles mixtes
Une fois XLSTAT lancé, choisissez XLSTAT / Modélisation des données/ Modèles Mixtes (voir ci-dessous).
 Une fois le bouton cliqué, la boîte de dialogue correspondant aux modèles mixtes apparaît. Dans le premier onglet, vous pouvez sélectionner les données sur la feuille Excel.
Une fois le bouton cliqué, la boîte de dialogue correspondant aux modèles mixtes apparaît. Dans le premier onglet, vous pouvez sélectionner les données sur la feuille Excel.
La Variable dépendante correspond à la variable à expliquer (ou variable à modéliser), qui est dans ce cas précis le score (dv). Toutes les variables restantes sont des variables explicatives qualitatives, sélectionnez les 3 variables "sujet", "temps" et "groupe".
L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.
 Dans l'onglet Options, vous pouvez sélectionner la structure de la matrice de covariance des erreurs e et des effets aléatoires g(pour des détails sur les options de cet onglet, voir l’aide d’XLSTAT).
Sélectionnez la structure composante de la variance pour les effets aléatoires (les résidus ont la même structure de covariance par défaut). Nous choisissons la contrainte a1=0, ce qui implique que le modèle s'écrira de façon à considérer que le groupe des contrôles (group=1) aura l'effet de base.
Appliquer une contrainte en ANOVA est indispensable pour des raisons théoriques, mais cela ne change ni les résultats, ni la qualité de l'analyse.
Par ailleurs, nous allons prendre en compte des interactions, il faut donc activer l’option interactions.
Nous activons également l’option t-tests Satterthwaite afin d’utiliser l’approximation de Satterthwaite pour le terme d’erreur du modèle.
Dans l'onglet Options, vous pouvez sélectionner la structure de la matrice de covariance des erreurs e et des effets aléatoires g(pour des détails sur les options de cet onglet, voir l’aide d’XLSTAT).
Sélectionnez la structure composante de la variance pour les effets aléatoires (les résidus ont la même structure de covariance par défaut). Nous choisissons la contrainte a1=0, ce qui implique que le modèle s'écrira de façon à considérer que le groupe des contrôles (group=1) aura l'effet de base.
Appliquer une contrainte en ANOVA est indispensable pour des raisons théoriques, mais cela ne change ni les résultats, ni la qualité de l'analyse.
Par ailleurs, nous allons prendre en compte des interactions, il faut donc activer l’option interactions.
Nous activons également l’option t-tests Satterthwaite afin d’utiliser l’approximation de Satterthwaite pour le terme d’erreur du modèle.
 Une fois que vous cliquez sur OK, une nouvelle fenêtre permettant de sélectionner les effets fixes ainsi que les effets aléatoires apparaît :
Une fois que vous cliquez sur OK, une nouvelle fenêtre permettant de sélectionner les effets fixes ainsi que les effets aléatoires apparaît :
 Nous voulons effectuer une ANOVA à mesures répétées en utilisant comme effets fixes les variables "temps", "groupe" et l’interaction "temps*groupe" et comme effets aléatoires la variable « sujet »
Une fois que vous cliquez sur OK, les calculs reprennent et les résultats sont affichés.
Nous voulons effectuer une ANOVA à mesures répétées en utilisant comme effets fixes les variables "temps", "groupe" et l’interaction "temps*groupe" et comme effets aléatoires la variable « sujet »
Une fois que vous cliquez sur OK, les calculs reprennent et les résultats sont affichés.
Interpréter une ANOVA à mesures répétées non équilibrée avec les modèles mixtes
Le premier tableau de résultats fournit les coefficients d'ajustement ainsi que des informations associées aux données.
 Les coefficients du modèle sont obtenus en utilisant le maximum de vraisemblance restreint (REML), on obtient donc des indices différents de ceux de l’ANOVA classique. Les AIC, AICC, SBC et CAIC sont des indices qui permettent de comparer des modèles en utilisant différentes structures de matrices de covariance.
Le tableau suivant donne les paramètres des matrices de covariance de l’effet aléatoire et des erreurs (structures composantes de la variance). Les p-valeurs des différents tests Z (Pr > Z) des tables ci-dessous nous indiquent une bonne fiabilité de l’estimation de l’erreur standard des paramètres aléatoires du modèle. Nous remarquerons toutefois que l’erreur standard de chaque paramètre demeure élevée sans doute en raison de la faible taille de l’échantillon.
Les coefficients du modèle sont obtenus en utilisant le maximum de vraisemblance restreint (REML), on obtient donc des indices différents de ceux de l’ANOVA classique. Les AIC, AICC, SBC et CAIC sont des indices qui permettent de comparer des modèles en utilisant différentes structures de matrices de covariance.
Le tableau suivant donne les paramètres des matrices de covariance de l’effet aléatoire et des erreurs (structures composantes de la variance). Les p-valeurs des différents tests Z (Pr > Z) des tables ci-dessous nous indiquent une bonne fiabilité de l’estimation de l’erreur standard des paramètres aléatoires du modèle. Nous remarquerons toutefois que l’erreur standard de chaque paramètre demeure élevée sans doute en raison de la faible taille de l’échantillon.
 Le tableau des tests de type III des effets fixes permet de vérifier la significativité des effets fixes en utilisant un test F de Fisher. Nous voyons donc ici que tous les effets fixes sont significatifs. Le temps écoulé a l’effet le plus important.
Le tableau des tests de type III des effets fixes permet de vérifier la significativité des effets fixes en utilisant un test F de Fisher. Nous voyons donc ici que tous les effets fixes sont significatifs. Le temps écoulé a l’effet le plus important.
La méthode d’approximation de Satterthwaite a été utilisée pour le calcul des degrés de liberté du dénominateur ainsi que de la statistique F afin de calculer une pvaleur (Pr > F) plus précise et diminuer ainsi l’erreur de type I sur l’hypothèse testée (égalité de la différence des « Moyennes Estimées »)
 Dans les cas déséquilibrés, les tests pour les termes d’ordre supérieur sont toujours les mêmes (ici l’effet d’interaction « temps*groupe »), alors que pour les termes d’ordre inférieur (« temps » & « groupe »), les hypothèses diffèrent entre les types. Dans notre exemple, les hypothèses types I et II deviennent dépendantes du nombre d’observations (unités expérimentales) à chaque combinaison de niveaux de facteur, de sorte que les hypothèses pour ces types deviennent difficiles à interpréter.
Au contraire, le test d’hypothèse de type III, que les données soient équilibrées ou non, teste toujours l’effet fixe considéré en contrôlant l’effet des autres facteurs du modèles (via une décomposition orthogonale) ce qui lui confère de bonnes propriétés quant à l’étude des jeux de données non équilibrés.
Ainsi, nous pouvons donc dire en conclusion que le traitement (variable groupe) et le temps écoulé ont des effets sur le niveau de dépression des patients.
Dans les cas déséquilibrés, les tests pour les termes d’ordre supérieur sont toujours les mêmes (ici l’effet d’interaction « temps*groupe »), alors que pour les termes d’ordre inférieur (« temps » & « groupe »), les hypothèses diffèrent entre les types. Dans notre exemple, les hypothèses types I et II deviennent dépendantes du nombre d’observations (unités expérimentales) à chaque combinaison de niveaux de facteur, de sorte que les hypothèses pour ces types deviennent difficiles à interpréter.
Au contraire, le test d’hypothèse de type III, que les données soient équilibrées ou non, teste toujours l’effet fixe considéré en contrôlant l’effet des autres facteurs du modèles (via une décomposition orthogonale) ce qui lui confère de bonnes propriétés quant à l’étude des jeux de données non équilibrés.
Ainsi, nous pouvons donc dire en conclusion que le traitement (variable groupe) et le temps écoulé ont des effets sur le niveau de dépression des patients.
Le tableau suivant rassemble les paramètres du modèle, leur écart-type ainsi qu’un intervalle de confiance. Ces paramètres s’interprètent de la même façon que dans le cas d’une analyse de la variance classique.
Ici, les tests t de Student sur la non nullité des coefficients de régression ne suivent pas exactement une loi de Student. Les résultats présentés dans la table ci-dessous se rapprochent toutefois de la distribution de t sous l’hypothèse nulle basée sur l’approximation de Satterthwaite des degrés de liberté des erreurs.
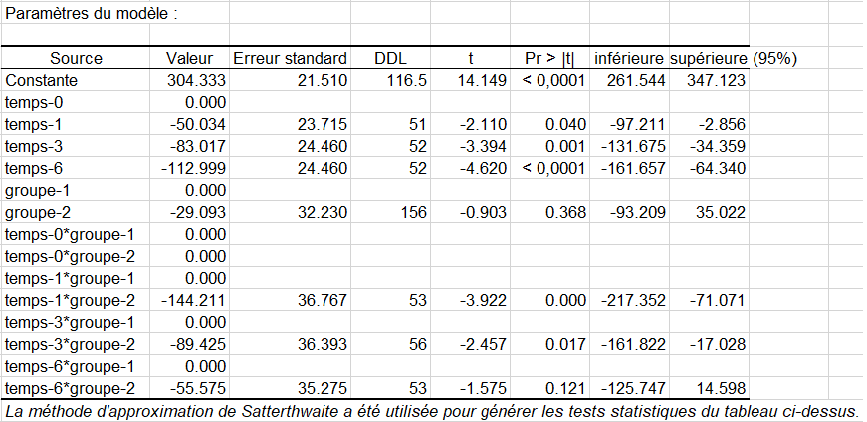 Nous remarquons en analysant les paramètres du modèle qu'aux temps 1, 3 et 6, l’effet sur le score est négatif et que le fait de subir un traitement (effet « groupe ») a un effet négatif sur le score (cela diminue donc la dépression du patient)
Nous remarquons en analysant les paramètres du modèle qu'aux temps 1, 3 et 6, l’effet sur le score est négatif et que le fait de subir un traitement (effet « groupe ») a un effet négatif sur le score (cela diminue donc la dépression du patient)
Ainsi, nous avons pu réaliser une ANOVA à mesures répétées avec les modèles mixtes malgré le fait que le jeu de données de l’étude ne respecte pas les conditions requises (nombre strictement identique de répétitions par sujet). De plus, l’approximation de Satterthwaite sur les erreurs du modèle nous garantit des résultats encore plus fiables pour les différents tests statistiques calculés (Type I, II, III et tests-t).
Cet article vous a t-il été utile ?
- Oui
- Non