ANOVA mit wiederholten Messungen in Excel erstellen
Dieses Tutorium wird Ihnen helfen, eine ANOVA mit wiederholten Messungen in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.
Datensatz für die Durchführung einer ANOVA mit wiederholten Messungen
Die Daten stammen aus einem Experiment, in dem eine Behandlungsmethode von Depressionen untersucht wird. Es wurden zwei verschiedene Patientengruppen (1 Kontrollpatienten / 2 Patienten in Behandlung) zu fünf verschiedenen Zeiten beobachtet (0: vor dem Test, 1: ein Monat nach dem Test, 3: 3 Monate nach Behandlung und 6: 6 Monate nach Behandlung). Bei der abhängigen Variable handelt es sich um ein Depressionspotential.
Es wurde eine ANOVA mit wiederholten Messungen durchgeführt, um die Wirkung der Behandlung und die zeitliche Auswirkung auf das Depressionspotential zu bestimmen. Beim ANOVA-Modell mit wiederholten Messungen und dem klassischen ANOVA-Modell mit Interaktionen handelt es sich um das gleiche Modell:
![]()
Es gibt einen festen Faktor (Gruppe). Der Unterschied zwischen der klassischen ANOVA und der ANOVA mit wiederholten Messungen besteht darin, dass die Messwerte desselben Patienten zu verschiedenen Zeiten nicht unabhängig sein dürfen. Dies führt dazu, dass die Kovarianz-Matrix der Fehler nicht diagonal ist.
Ziel dieses Tutorials
In diesem Tutorial verwenden wir die Methode der kleinsten Quadrate zur Schätzung des Modells. Die Kovarianzmatrix soll sphärisch sein.
Diese Methode ist sehr einfach: Zunächst wird auf jede Messung eine klassische ANOVA angewendet. Die Ergebnisse entsprechen denen einer klassischen Varianzanalyse. Anschließend erhalten wir die Ergebnisse der Kovarianz-Matrix und des Wiederholungsfaktors.
Sie können auch eine andere Form der Kovarianz-Matrix mit XLSTAT verwenden, z. B. gemischte Modelle. Ziehen Sie bitte das folgende Tutorial zurate, um ein Beispiel zu erhalten.
Datenstruktur
Daten können auf zwei Arten dargestellt werden. Die klassische Darstellungsweise ist eine Spalte pro Wiederholung. Das heißt, die Daten jeder wiederholten Messung einer abhängigen Variable werden in einer separaten Spalte dargestellt.
Einrichten einer ANOVA mit wiederholten Messungen
Wählen Sie nach dem Öffnen von XLSTAT den Befehl XLSTAT / Modellierung der Daten / ANOVA mit wiederholten Messungen aus, oder klicken Sie auf die entsprechende Schaltfläche der Symbolleiste Modellierung der Daten (siehe unten).
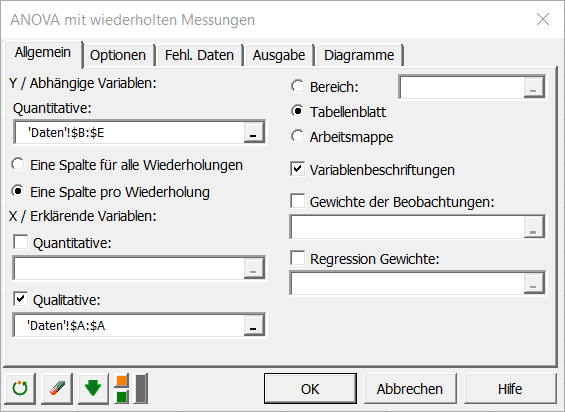
Durch Anklicken der Schaltfläche wird das Dialogfenster "ANOVA mit wiederholten Messungen" angezeigt. Wählen Sie die Daten in der Excel-Tabelle aus.
In diesem Beispiel ist "dv0-dv1-dv3-dv6" die abhängige Variable (oder zu modellierende Variable).
Es ist unser Ziel, die Auswirkung der Gruppe auf die Varianz des Depressionspotentials zu bestimmen.
Bei der Auswahl der Spaltentitel der Variablen haben wir die Option Variablenbeschriftungen aktiviert.
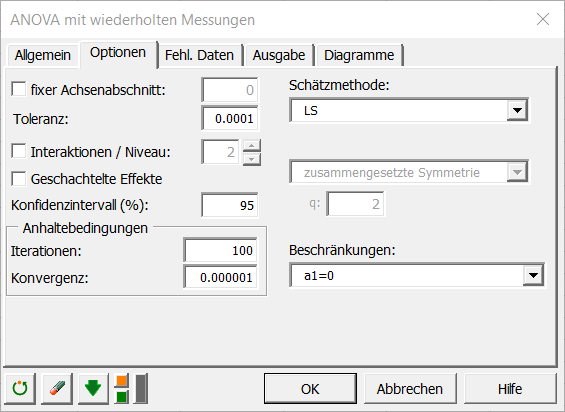
Im Reiter Optionen wählen wir LS (kleinste Quadrate) als Schätzmethode aus.
Für die Option "Beschränkung" behalten wir a1=0 bei, das heißt, dass unser Modell auf der Annahme erstellt wird, dass die Kontrollgruppe die Standardauswirkung auf die Wertung hat.
Obwohl bei der ANOVA aus theoretischen Gründen eine Beschränkung auf das Modell angewendet werden muss, hat dies keine Auswirkungen auf das Ergebnis (Anpassungsgüte). Der einzige Unterschied besteht beim eigentlichen Schreiben des Modells.
Die ausgewählten Ausgaben sind:
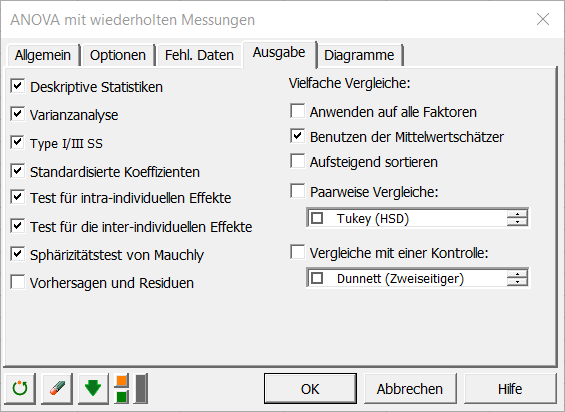
Sobald Sie auf die Schaltfläche OK klicken, erscheint ein Dialogfenster, in dem Sie wählen können, welche Faktoren im Modell berücksichtigt werden müssen. Der fixe Effekt ist "Gruppe", der wiederholte Faktor ist "Wiederholung", und der Subjektfaktor ist "Subjekt" (diese Faktoren werden automatisch erzeugt).
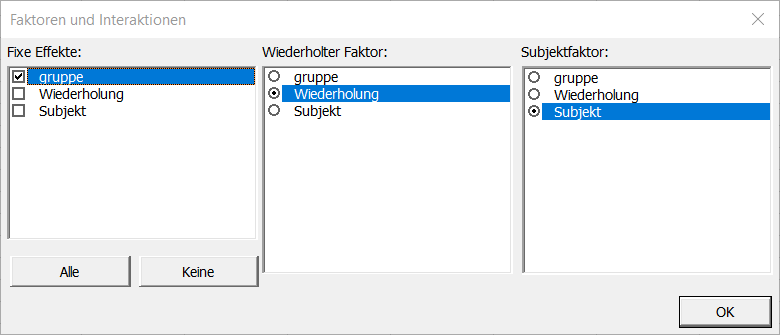
Hinweis: Ein Faktor kann nicht gleichzeitig Subjektfaktor oder wiederholter Faktor und fixer Effekt sein.
Die Berechnung wird gestartet, sobald Sie auf die Schaltfläche OK klicken. Die Ergebnisse werden anschließend angezeigt.
Interpretation der Ergebnisse einer ANOVA mit wiederholten Messungen
Bei den ersten von XLSTAT angezeigten Ergebnissen handelt es sich um die grundlegenden mit der abhängigen Variable verknüpften Statistiken.

Es wurde für jede Messung eine ANOVA durchgeführt. Es werden die Ergebnisse für die Zeiten 0, 1, 3 und 6 angezeigt. Weitere Informationen erhalten Sie im Tutorial zur einfachen ANOVA.
Die Varianzanalyse für die Tabelle "vor dem Test" (dv0) lautet:

Die Varianzanalyse für die Tabelle "ein Monat nach dem Test" (dv1) lautet:

Die Varianzanalyse für die Tabelle "3 Monate nach Behandlung" (dv3) lautet:

Die Varianzanalyse für die Tabelle "6 Monate nach Behandlung" (dv6) lautet:

Es lässt sich feststellen, dass der Effekt der Gruppe auf das Depressionspotenzial nach einem Monat nach der Behandlung wesentlich größer als 0 ist.
Im Anschluss an die vier Analysen werden zusätzliche mit dem wiederholten Design verbundene Ausgaben angezeigt.
Die erste Tabelle ist sehr wichtig und hilft bei der Validierung der Spherizität der Kovarianzmatrix der Fehler. Dieser Test wird als Sphärizitätstest von Mauchly bezeichnet.

Wir können sehen, dass der p-Wert kleiner als 0,05 ist, woraus wir erschließen können, dass die Kovarianzmatrix sphärisch ist. Zusätzlich zum Test von Mauchly wird das Greenhouse-Geisser Epsilon und Huynt-Feldt Epsilon angezeigt. Je näher diese bei 1 liegen, desto sphärischer ist die Kovarianzmatrix. In unserem Beispiel wurde die Hypothese der Spherizität validiert.


Nun können die folgenden zwei Tabellen analysiert werden. Zunächst analysieren wir den Test für die inter-individuellen Effekte, der den Effekt der Gruppenvariable auf den gesamten Datensatz zeigt, ohne die Wiederholungen (oder Messwerte) zu berücksichtigen. Wir erkennen, dass die Gruppe einen signifikanten Einfluss auf das Depressionspotential hat. Anschließend analysieren wir den Test für intra-individuelle Effekte. Dieser zeigt die Auswirkung der Zeit (der verschiedenen Messwerte) auf die abhängige Variable. Es kann hilfreich sein, die Interaktionen zwischen der Wiederholung und den erklärenden Faktoren näher zu betrachten. Es ist zu sehen, dass der Wiederholungsfaktor einen signifikanten Einfluss auf das Depressionspotential hat, ebenso wie die Interaktion.
Diese Studie hat gezeigt, dass sowohl die Zeit als auch die Behandlung einen signifikanten Einfluss auf das Depressionspotential hat.
Weitere in XLSTAT verfügbare Ergebnisse können ebenfalls hilfreich sein: Residuen, Residuendiagramme, Diagramme von Mittelwerten der kleinsten Quadrate, multiples Testen von Mittelwerten, ...
War dieser Artikel nützlich?
- Ja
- Nein