ANOVA de medidas repetidas: tutorial en Excel

Este tutorial le mostrará cómo configurar e interpretar un ANOVA de medidas repetidas en Excel usando el software XLSTAT.

Datos para ejecutar un ANOVA de medidas repetidas

Descargar los datos

Los datos corresponden a un experimento en el que se estudia un tratamiento para la depresión. Se ha llevado a cabo un seguimiento de dos grupos de pacientes (1: control / 2: tratamiento) en cinco ocasiones diferentes: (0: pre-test, 1: post-test después de un mes, 3: 3 meses de seguimiento y 6: 6 meses de seguimiento). La variable dependiente es la puntuación en depresión.

Hemos llevaro a cabo un ANOVA de medidas repetidas con el fin de determinar el efecto del tratamiento y el efecto del tiempo sobre la puntuación en depresión. El modelo ANOVA de medidas repetidas es el mismo que el modelo ANOVA clásoco con interacciones.

Tenemos un factor fijo (grupo), un factor-sujeto (los pacientes) y la repetición de las medidas. La interacción entre el grupo y la repetición se incluye en el modelo. La diferencia entre el ANOVA clásico y el ANOVA de medidas repetidas es que no se supone que las medidas sobre el mismo patiente sean independientes y, en consecuencia, la matriz de covarianzas de los errores no es diagonal.

Objetivo de este tutorial

En este tutorial, usamos el método de estimación de mínimos cuadrados (least squares, LS) para estimar el modelo. Suponemos que la matriz de varianzas-covarianzas es esférica. El método es muy simple: en primer lugar, se lleva a cabo un ANOVA clásico sobre cada momento evaluado. Los resultados son los mismos que en el análisis de varianza clásico. A continuación, se proporcional los resultados basados en la matriz de covarianzas y en el factor de repetición. Podemos usar otra forma de matriz de covarianzas con XLSTAT utilizando modelos mixtos. Por favor, consulte el siguiente tutorial si desea ver un ejemplo.

Estructura de los datos

Los datos pueden presentarse usando dos formatos. El clásico es usar una columna por repetición. Esto significa que por cada medida repetida de la variable dependiente debe haber una columna.

Configuración de un ANOVA de medidas repetidas

Tras abrir XLSTAT, seleccione el comando XLSTAT / Modelación de datos / ANOVA de medidas repetidas, o bien haga clic en el botón correspondiente de la barra de herramientas Modelación de datos (véase más abajo).

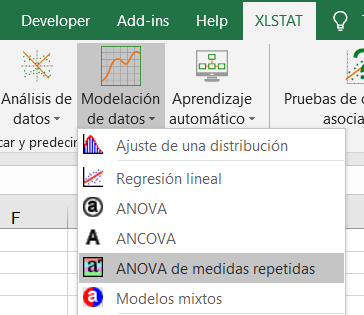
Tras hacer clic en el botón, aparece el cuadro de diálogo ANOVA de medidas repetidas. Seleccione los datos en la hoja de Excel.

La Variable dependiente (o variable a modelar) es aquí “dv0-dv1-dv3-dv6”.

Nuestro objetivo se centra en determinar el efecto del grupo sobre la variabilidad de la puntuación en depresión.

Puesto que hemos seleccionado el título de las columnas de las variables, dejamos activada la opción Etiquetas de las variables.

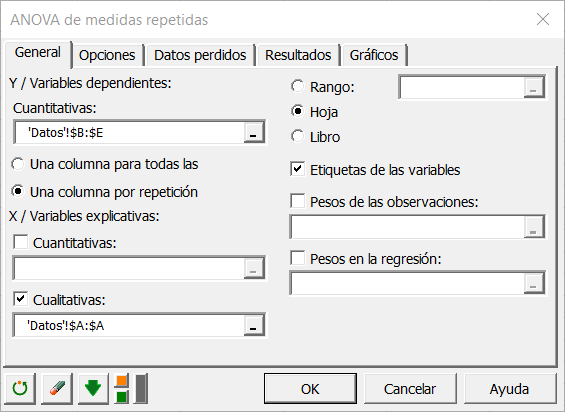
En la pestaña Opciones, seleccionamos LS (Least Squares) como método de estimación (mínimos cuadrados).

Hemos dejado la opción de restricción en a1=0, lo que significa que queremos que el modelo se construya sobre la asunción de que el grupo de control tiene el efecto estándar sobre la puntuación.

A pesar de que tenemos que aplicar una restricción al modelo de ANOVA por razones teóricas, ello no afectará a los resultados (bondad de ajuste). La única diferencia afecta a la escritura real del modelo.

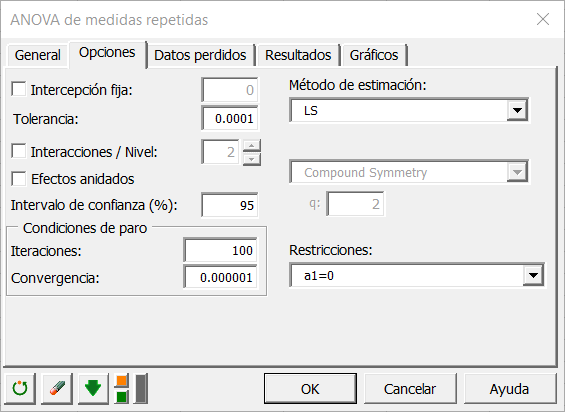
Los resultados seleccionados son los siguientes:

Una vez que haya hecho clic en el botón OK, aparece un cuadro de diálogo para que pueda elegir qué factores tienen que tenerse en cuenta en el modelo. El efecto fijo es el grupo, el factor repetido es la repetición y el factor sujeto es el sujeto (estos factores se generan de forma automática).

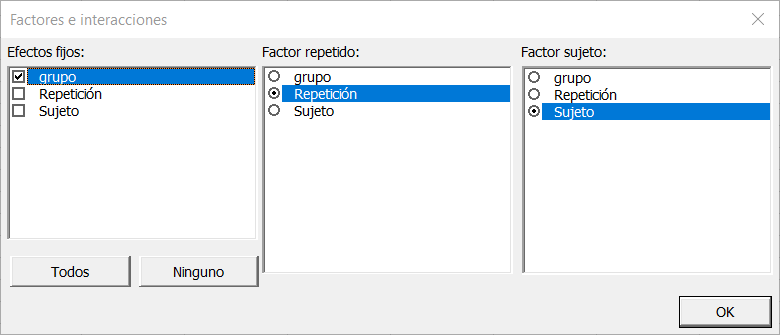
Nota: Un factor no puede ser factor-sujeto o factor-repetido y factor-fijo al mismo tiempo.

Tras hacer clic en el botón OK, comienzan los cálculos. A continuación se muestran los resultados.

Interpretación de los resultados de un ANOVA de medidas repetidas

El primer resultado mostrado por XLSTAT corresponde a los estadísticos básicos asociados a la variable dependiente.

Se lleva a cabo un ANOVA para cada medida. Se muestran los resultados asociados a los momentos 0, 1, 3 y 6. Si desea más detalles, puede consultar este tutorial sobre ANOVA unifactorial. La tabla de análisis de varianza pre-test (dv0) es:

La tabla de análisis de varianza del post-test (un mes) (dv1) es:

The analysis of variance table 3 months follow-up (dv3) is:

La tabla de análisis de varianza del seguimiento (seis meses) (dv6) es:

Podemos ver que el grupo tiene un efecto significativamente mayor que 0 en la puntuación en depresión después de 1 mes de tratamiento.

Una vez se han realizado los cuatro análisis, se muestran algunos resultados adicionales relacionados con el diseño de medidas repetidas.

La primera tabla es muy importante y ayuda a validar la esfericidad de la matriz de covarianzas de los errores. Esta prueba se conoce como prueba de Mauchly.

Teniendo en cuenta que el valor de p es menor que 0.05 (alfa), podemos rechazar la hipótesis nula y aceptar la hipótesis alternativa de que la matriz de la covarianza no es esférica. Aquí se han aplicado las correcciones de Greenhouse-Geisser y de Huynt-Feldt para ajustar el valor de p. Cada una de estas correcciones estima un estadístico denominado epsilon. Cuanto más se acerca a uno, más esférica es la matriz de covarianza.

Ahora podemos analizar las dos tablas siguientes. En primer lugar, las pruebas sobre los efectos inter-sujetos que muestran el efecto de la variable grupo en el conjunto de datos sin tener en cuenta las repeticiones (o medidas). Vemos que el grupo tiene un impacto significativo en la puntuación en depresión. A continuación, las pruebas sobre los efectos intra-sujetos muestran el impacto del tiempo (de las diferentes medidas) sobre la variable dependiente. Puede ser útil examinar los términos de interacción entre la repetición y los factores explicativos. Vemos que el factor de repetición tiene un impacto significativo en la puntuación en depresión; la interacción tiene también un impacto significativo.

Este estudio ha mostrado que tanto el tiempo como el tratamiento tienen un impacto significativo en la puntuación en depresión.

Algunos otros resultados pueden ser útiles y están disponibles en XLSTAT: residuos, gráficos de residuos, gráficos de medias de mínimos cuadrados, comparaciones de medias múltiples comparaciones...