Test de Kolmogorov-Smirnov dans Excel

Exécution et interprétation du test non-paramétrique de Kolmogorov-Smirnov pour comparer deux distributions dans Excel avec XLSTAT.

Jeu de données pour le test de Kolmogorov-Smirnov dans Excel avec XLSTAT

Le jeu de données correspond à des scores (0 - 30) mesurant la qualité de deux marques de chaussures (A et B). Les scores sont la synthèse de réponses à des questionnaires remplis par des clients utilisant une marque ou l’autre. 15 clients ont répondu pour la marque A et 8 clients (différents) ont répondu pour la marque B.

But de ce tutoriel

Ce tutoriel est divisé en deux parties :

Dans la première partie, nous comparons les distributions des deux échantillons sans faire d’hypothèse sur des distributions théoriques sous-jacentes (exemple : distribution normale). Le test non-paramétrique de Kolmogorov-Smirnov est adapté à cette problématique et sera utilisé.

Dans la deuxième partie, nous utilisons le test de Kolmogorov-Smirnov pour comparer la distribution d’un échantillon à une distribution théorique.

Partie 1 : Test de Kolmogorov-Smirnov pour la comparaison des distributions de deux échantillons

Nous nous intéressons à comparer les distributions des deux échantillons de scores.

Tout d’abord, comparons graphiquement ces deux distributions en inspectant les histogrammes : XLSTAT / visualisation des données / Histogrammes. Sélectionner les deux colonnes d’intérêt dans la plage Données de l’onglet Général. Puis dans l’onglet Options, cocher minimum et taper 0 dans la case à côté. Cette option produira des histogrammes ayant le même point d’origine (0) sur l’axe des abscisses, et facilitera ainsi la comparaison des deux distributions. Cliquer sur OK.

Les histogrammes apparaissent dans la feuille de résultats:

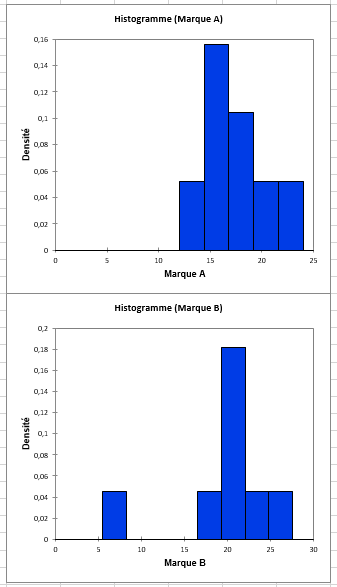
Sans faire d’hypothèse sur des distributions théoriques, nous pouvons dire que la distribution des scores de l’échantillon B semble un peu plus étalée vers des valeurs faibles en comparaison avec la distribution des scores de l’échantillon A. Utilisons le test non-paramétrique de Kolmogorov-Smirnov pour comparer ces deux distributions : XLSTAT / Tests non paramétriques / Comparaison de deux distributions.

Sélectionner la colonne Marque A dans la plage de l’échantillon 1 et Marque B dans la plage de l’échantillon 2. Noter que le test de Kolmogorov-Smirnov peut fonctionner avec des données déséquilibrées (c’est le cas de nos données : il y a moins de mesures pour la marque B que pour la marque A). Dans l’onglet Options, noter aussi qu’il est possible d’opter pour une hypothèse alternative unilatérale (ce qui est peu courant) et/ou pour un calcul exact de la p-value. Dans l’onglet Graphiques, cocher la case Histogrammes cumulés. Cliquer sur OK.

La feuille de résultats contient notamment la statistique du test de Kolmogorov-Smirnov (0.475) que l’on peut retrouver grâce au graphique de fréquence cumulée (voir plus bas). Cette statistique est associée à une p-value (0.133) indiquant que les deux distributions ne sont pas significativement différentes au seuil alpha = 0.05.

Le graphique de fréquence cumulée présente la mesure étudiée (scores) sur l’axe des abscisses. Pour un point donné sur l’axe des abscisses, la fréquence cumulée correspond à la proportion de scores situés en-dessous de ce point parmi les scores de la Marque en question. Ainsi, comme nous l’avaient suggéré les histogrammes, nous remarquons un « début de cumul de scores » plus précoce pour la marque B que pour la marque A le long de l’axe des abscisses. Inspectons à présent les médianes, qui correspondent aux scores pour une fréquence cumulée de 0.5. La médiane des scores de la marque B (20 environ) semble plus élevée que celle de la marque A (17 environ).

La statistique D du test de Kolmogorov-Smirnov correspond à l’écart le plus élevé entre les deux courbes. Ici, cet écart coïncide avec des valeurs médianes, mais ceci n’est pas systématique. Plus cet écart est élevé, plus la p-value associée sera faible, et plus les deux distributions seront significativement différentes.

Partie 2 : Test de Kolmogorov-Smirnov pour la comparaison d’une distribution observée à une distribution théorique

Supposons que les scores de qualité des chaussures de la marque A ont été obtenus en France. Aux Etats-Unis, ce score suit une distribution normale de moyenne 21.5 et d’écart-type 2.3. Nous cherchons à savoir si la distribution des scores en France diffère significativement de la distribution théorique des scores aux Etats-Unis. Nous utiliserons là encore le test de Kolmogorov-Smirnov. La seule différence avec la partie précédente est que nous cherchons à comparer une distribution observée à une distribution théorique plutôt que comparer deux distributions observées.

Allez dans XLSTAT / Tests non paramétriques / Ajustement d’une loi de probabilité. Dans l’onglet Général, sélectionner les données correspondant à la marque A, choisir la distribution normale, cocher la case saisir et saisir les paramètres : µ = 21.5 et sigma = 2.3. Dans l'onglet Graphiques, cocher Histogrammes cumulés. Cliquer sur OK.

Dans la feuille de résultats, l’histogramme suggère un décalage vers des valeurs faibles de la distribution des données françaises par rapport à la distribution théorique des scores obtenus aux Etats-Unis (ligne rouge).

Le test de Kolmogorov-Smirnov renvoie une p-value de 0.000 indiquant que la distribution observée (données) est très significativement différente de la distribution théorique au seuil alpha = 0.05.

N'hésitez pas à consulter notre guide de choix de test statistique.