Test de Wilcoxon pour un échantillon dans Excel
Ce tutoriel explique comment mettre en place et interpréter un test des rangs signés de Wilcoxon pour un échantillon dans Excel avec le logiciel XLSTAT.
Jeu de données pour réaliser un test de Wilcoxon pour un échantillon
Les données correspondent à une étude lors de laquelle une nouvelle marque de chips a été évaluée par 30 consommateurs. Chaque consommateur a indiqué sa préférence sur une échelle de 1 à 10. Nous souhaitons déterminer si la noté médiane de préférence est supérieure à 7 correspondant à la note médiane pour la marque concurrente.
Dans cet objectif, nous allons utiliser le test des rangs signés de Wilcoxon pour un échantillon. Ce test permet de comparer la médiane d’un échantillon à une valeur théorique sans supposer la normalité de l’échantillon. C’est une alternative non-paramétrique au test de Student.
Les données sont fictives et ont été créées pour ce tutoriel.
Paramétrer un test de Wilcoxon pour un échantillon avec XLSTAT
Une fois que XLSTAT est activé, cliquez sur le menu XLSTAT / Tests non paramétriques / Test des rangs signés de Wilcoxon pour un échantillon.
 Une fois le bouton cliqué, la boîte de dialogue apparaît.
Une fois le bouton cliqué, la boîte de dialogue apparaît. Sélectionnez la variable Notes dans le champ Echantillons.
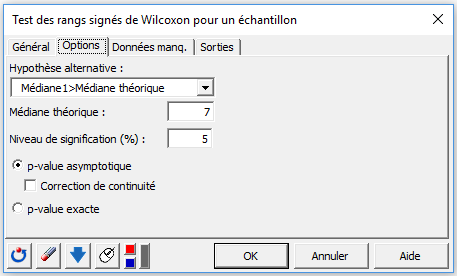
Dans l’onglet Options, choisissez Médiane>Médiane Théorique comme hypothèse alternative et rentrez la valeur 7 dans le champ Médiane théorique. L’hypothèse alternative, ici, indique un test unilatéral à droite.
La p-value sera obtenue grâce à une approximation asymptotique distribution de la statistique calculée.
Sélectionnez la variable Notes dans le champ Echantillons.
Dans l’onglet Options, choisissez Médiane>Médiane Théorique comme hypothèse alternative et rentrez la valeur 7 dans le champ Médiane théorique. L’hypothèse alternative, ici, indique un test unilatéral à droite.
La p-value sera obtenue grâce à une approximation asymptotique distribution de la statistique calculée.
 Les calculs commencent lorsque vous cliquez sur le bouton OK puis les résultats sont affichés.
Les calculs commencent lorsque vous cliquez sur le bouton OK puis les résultats sont affichés.
Interprétation d’un test de Wilcoxon pour un échantillon
Dans le tableau sont affichées les résultats du test : la statistique V de Wilcoxon, le z-score (V standardisé) et la p-value correspondante.
La p-value nous indique que la probabilité de rejeter l'hypothèse nulle alors qu'elle est vraie est inférieure au niveau de signification alpha (= 0.05). Dans ce cas, nous pouvons rejeter l’hypothèse nulle d’absence de différence significative entre les deux médianes.
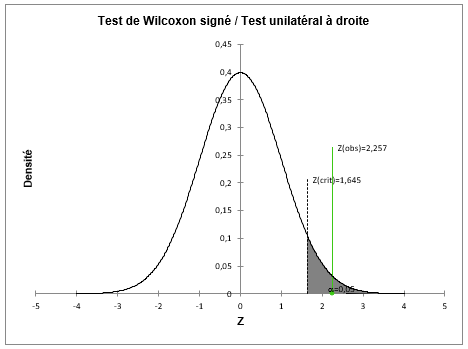
Le graphique ci-dessous confirme la conclusion au-dessus puisque le Z (=2.257) est supérieur à la valeur critique (=1.645).
Cet article vous a t-il été utile ?
- Oui
- Non
