Régression non paramétrique (kernel et Lowess) dans Excel

Ce tutoriel explique comment calculer et interpréter une régression non paramétrique de type kernel avec Excel en utilisant XLSTAT.

Régression non paramétrique : kernel regression

La Kernel Regression qui fait partie des méthodes de régression non-paramétrique est aussi parfois associée aux méthodes de lissage. En principe, l'utilisation de la régression Kernel se fait suivant trois phases :

1. une phase d’ajustement pendant laquelle on va essayer de trouver la meilleure combinaisons des caractéristiques de la méthode (modèle, noyau, bande passante, ...) sur un échantillon test;
2. une phase de validation qui permet de valider le modèle sur de nouvelles observations;
3. une phase d'application une fois que la validation est satisfaisante.

Remarque : la méthode de régression non paramétrique inclut par nature une validation, puisque l'observation pour laquelle on fait une prévision n'est pas incluse dans le jeu de données servant à sa prévision. Néanmoins, on pourra vouloir valider la méthode en l'appliquant à un nouveau jeu de données correspondant par exemple à une période de temps différente. Les prévisions pour l'échantillon de validation pourront alors être obtenues sur la base de l'échantillon de départ. Un bon ajustement pourra permettre de conclure que les deux périodes de temps sont homogènes et que la méthode est donc validée.

Contrairement à la régression linéaire classique, le but n'est pas ici de trouver un modèle unique décrivant/expliquant/prédisant un phénomène, mais d'obtenir une méthode prévisionnelle efficace, sans qu'une compréhension physique du phénomène soit nécessaire.

La régression non-paramétrique fonctionne un peu comme une boîte noire.

C'est une méthode intensive, puisque pour chaque observation, un nouveau modèle est calculé (en Robust Lowess regression, on calcule jusqu'à 3 modèles par observation).

Jeu de données pour la régression non paramétrique de type kernel

L'exemple traité ici correspond à un phénomène simple et n'a qu'un but illustratif. La régression non paramétrique peut s'avérer très utile pour modéliser des phénomènes complexes comme des séries chronologiques en finance ou la pollution de l'air en milieu urbain. Elle est aussi parfois utilisée comme méthode de lissage.

L'exemple développé ci-dessous porte sur les données utilisées dans le tutoriel sur la régression linéaire classique.

Les données proviennent de [Lewis T. and Taylor L.R. (1967). Introduction to Experimental Ecology, New York: Academic Press, Inc.]. Les données concernent 237 enfants, décrits par leur sexe, leur âge en mois, leur taille en inch (1 inch = 2.54 cm), et leur poids en livres (1 livre = 0.45 kg). L'étude comporte deux phases : une phase d'ajustement sur 217 individus, et une phase de validation de 20 individus (10 femmes et 10 hommes).

Paramétrer une régression non paramétrique de type kernel

Une fois XLSTAT lancé, choisissez la commande XLSTAT / Modélisation / Régression non paramétrique ou cliquez sur le bouton correspondant de la barre d'outils Modélisation.

Une fois le bouton cliqué, la boîte de dialogue correspondant à la régression non paramétrique apparaît.

Vous pouvez alors sélectionner les données sur la feuille Excel. La "Variable dépendante" correspond à la variable expliquée (ou variable à modéliser), qui est dans ce cas précis le poids.

Les variables explicatives sont ici la "taille", l'"âge" (données quantitatives) et le "sexe" (données qualitatives).

La sélection par colonnes est utilisée ici pour gagner du temps. L'option Libellés des variables est activée car la première ligne des colonnes comprend le nom des variables.

La méthode choisie est celle du modèle polynomial de degré 1, en utilisant tous les individus, sauf celui concerné pour calculer la prédiction, avec une pondération utilisant le noyau gaussien.

La bande-passante choisie est celle de l'écart-type. Cela permet d'éviter qu'un effet d'échelle perturbe les calculs.

Remarque : dans ce cas, on est très proche du modèle d'ANCOVA, la seule particularité étant que l'individu n'intervient pas dans le modèle utilisé pour établir la prédiction qui le concerne, et que le poids des individus dans le modèle dépend de leur distance à l'individu concerné.

Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.

Interpréter les résultats d'une régression non paramétrique de type kernel

Les coefficients d'ajustement du modèle permettent d'évaluer la performance du modèle, et éventuellement de la comparer à celles d'autres modèles.

Le R’² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, expliqué par les variables explicatives. Plus ce coefficient est proche de 1, meilleur est le modèle.

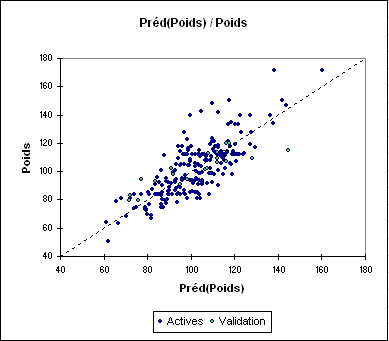
La tableau des prédictions et des résidus permet de visualiser pour chacun des individus, les données d'entrée, la prévision du modèle et le résidu. Les résidus varient en valeur absolue entre 0.01 (individu 45) et 40 (individu 195).

Pour les données de validation, on note que les résidus calculés sont fortement variables. Pour les individus 229 et 235 la prévision est très bonne. Elle l'est nettement moins pour l'individu 224.