Regresión no paramétrica (Kernel & Lowess)

Este tutorial le mostrará cómo configurar e interpretar una regresión no paramétrica (Kernel & Lowess) en Excel usando el software XLSTAT.

¿No está seguro de que esta sea la función de modelado que está buscando? Consulte por favor esta guía.

¿Qué es una Regresión Kernel?

La Regresión Kernel pertenece a la familia de métodos de regresión no paramétricos. En ocasiones se la relaciona con métodos de suavizado (smoothing). La regresión Kernel habitualmente se compone de tres fases: - un paso de ajuste en el que intentamos encontrar la mejor combinación de tipo de modelo, función kernel, y ancho de banda, utilizando una muestra de prueba.

• una fase de validación que permite validar el modelo sobre nuevas observaciones para las que se conoce una predicción;

• una fase de aplicación, en que el modelo se aplica a un nuevo conjunto de datos para los cuales se desconoce la predicción.

Nota: la regresión no paramétrica incluye una fase de validación puesto que una observación dada nunca se utiliza para construir el modelo que se usa para generar la predicción correspondiente. Sin embargo, todavía se puede aislar una sub-muestra que sólo se dedica a la fase de validación, para comprobar la robustez del modelo.
Al contrario de lo que sucede en la regresión lineal clásica, el objetivo no es encontrar un modelo único que describa / explique / prediga un fenómeno, sino obtener un método predictivo eficiente. La regresión no paramétrica es una especie de caja negra. Es numéricamente intensiva, puesto que para cada observación se calcula un nuevo modelo (en la regresión Lowess robusta, se calculan hasta tres modelos para cada observación).

Datos para la regresión kernel

El ejemplo que se trata en este tutorial corresponde a un caso muy sencillo, y el interés es sólo ilustrativo. La regresión no paramétrica puede ser muy útil para predecir fenómenos complejos, como las series temporales en las finanzas, la contaminación del aire de un día para el otro, o las ventas de trimestre a otro. A veces también se utiliza para suavizar una serie de datos.
El ejemplo utiliza los mismos datos utilizados para el tutorial sobre la regresión lineal.
Una hoja Excel que contiene los datos y los resultados para su uso en este tutorial se Los datos se han obtenido de [Lewis T. and Taylor L.R. (1967). Introduction to Experimental Ecology, New York: Academic Press, Inc.]. Conciernen a 237 niños, descritos por género (Gender), edad en meses (Age), altura en pulgadas (Height) (1 pulgada = 2.54 cm), y peso en libras (Weight) (1 libra = 0.45 kg).
El estudio está dividido en dos fases: una fase de ajuste en la que se usan 217 individuos, y una fase de validación con 20 individuos (10 mujeres y 10 varones).

Configuración de una regresión kernel

Tras abrir XLSTAT, seleccione el comando XLSTAT / Modelación de datos / Regresión no paramétrica, o bien haga clic en el botón correspondiente de la barra de herramientas Modelación de datos (véase más abajo).

Una vez que haya hecho clic en el botón, aparece el cuadro de diálogo de regresión no paramétrica. A continuación, puede seleccionar los datos en la hoja de cálculo de Excel.

La variable dependiente corresponde a la variable que necesita ser explicada (o la variable a modelar), que es aquí el "peso".

Las variables explicativas son la "altura" y la "edad" (datos cuantitativos) y el sexo (datos cualitativos).

La selección ha sido realizada por columnas, puesto que los datos comienzan en la primera fila. Se activa la opción Etiquetas de las variables, puesto que la primera fila se corresponde con el nombre de las variables.

Hemos optado por utilizar la función polinómica con grado 1, utilizando todos los datos (excepto el que se está prediciendo), con una ponderación basada en el kernel gaussiano, y un ancho de banda basado en la desviación estándar de las variables. Este último permite evitar efectos de escalamiento durante los cálculos.

Nota: estamos muy cerca del modelo ANCOVA, con la diferencia de que no utilizamos la observación en el modelo que se usa para hacer la predicción correspondiente, y que los pesos de las observaciones en el modelo dependen de su distancia a la observación a predecir.

Los cáculos comienzan tras hacer clic en OK. Los resultados se muestran a continuación.

Interpretación de los resultados de una regresión kernel

Los coeficientes de bondad del ajuste permiten evaluar el desempeño del modelo y comparar posiblemente varios modelos. El coeficiente de determinación (R’²) proporciona una idea del % de variabilidad de la variable peso que es explicada por las variables explicativas. Mientras más cercano esté R’² a 1, mejor es el modelo.

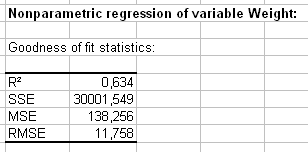
La tabla de las predicciones y los residuos permite visualizar para cada individuo los datos de entrada, la predicción y el residuo. Los residuos varían en valores absolutos entre 0.01 (individuo 45) y 40 (individuo 195). Para la validación de los datos que se muestran en la segunda parte de la tabla, nos damos cuenta de que los residuos varían también mucho. Para los individuos 229 y 235 la predicción es excelente. Es mucho peor para el individuo 224.