Regresión Mínimos Cuadrados Parciales PLS Excel

Este tutorial le mostrará cómo configurar e interpretar una Regresión por Mínimos Cuadrados Parciales (Partial Least Squares, PLS) en Excel usando el software XLSTAT.

Datos para ejecutar una regresión por Mínimos Cuadrados Parciales

Este tutorial se basa en datos que han sido extensamente analizados en [Tenenhaus, M., Pagès, J., Ambroisine L. and & Guinot, C. (2005); PLS methodology for studying relationships between hedonic judgements and product characteristics; Food Quality an Preference. 16, 4, pp 315-325].
Los datos usados en este artículo corresponden a 6 zumos de naranja descritos por 16 descriptores psico-químicos y evaluados por 96 jueces.

Objetivo de la regresión por Mínimos Cuadrados Parciales en este ejemplo

La regresión por mínimos cuadrados parciales nos permitirá obtener un mapa simultáneo de los jueces, los descriptores y los productos, y a continuación analizar, para algunos jueces, qué descriptores están relacionados con sus preferencias.

Configuración de una regresión por Mínimos Cuadrados Parciales

• Una vez que XLSTAT esté abierto, haga clic en Modelado de datos / Regresión PLS.

• Una vez que haya hecho clic en el botón, se mostrará el cuadro de diálogo de la regresión por Mínimos Cuadrados Parciales.

• En el campo Variable(s) dependiente(s), seleccione con el ratón las calificaciones de los 96 jueces.

• Las calificaciones son los "Ys" del modelo ya que queremos explicar las calificaciones dadas por los jueces.

• En el campo Variable(s) cuantitativa(s), seleccione las variables explicativas, que en nuestro caso son los descriptores fisicoquímicos.

• Los nombres de los jugos de naranja también se han seleccionado como Etiquetas de observación.

• En la pestaña Opciones del cuadro de diálogo, fijamos el número de componentes en 4 en las Condiciones de parada.

• Por último, en la pestaña Gráficos, se activó la opción Etiquetas coloreadas para facilitar la lectura de los gráficos. La opción Vectores se desmarcó para no saturar los gráficos.

• Los cálculos extremadamente rápidos comienzan cuando haga clic en Aceptar. La visualización de los resultados se detiene para permitirle seleccionar los ejes para los mapas.

• Luego, en el cuadro Seleccionar Ejes, solo tiene que hacer clic en Hecho para que los gráficos solo se muestren para los dos primeros ejes.

Interpretación de los resultados de una regresión por Mínimos Cuadrados Parciales

La visualización de los resultados tomará unos pocos segundos, ya que hay muchas tablas y gráficos debido a que tenemos 96 variables dependientes.

Después de las tablas que muestran los estadísticos básicos y las correlaciones entre todas las variables seleccionadas (las variables dependientes se muestran en azul y las variables explicativas cuantitativas en negro), se presentan los resultados específicos de la regresión PLS.

La primera tabla y su correspondiente gráfico de barras permiten visualizar la calidad de la regresión por mínimos cuadrados parciales como función del número de componentes.

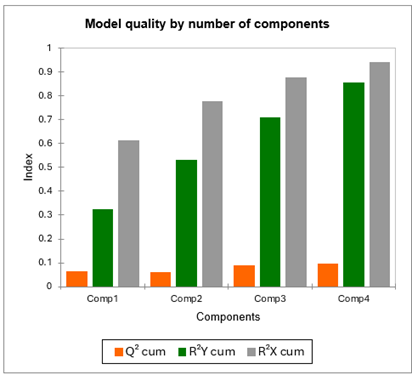
El índice acumulado Q² mide la bondad del ajuste global y la calidad predictiva de los 96 modelos.

XLSTAT ha seleccionado automáticamente 4 componentes. Vemos que Q² permanece bajo, incluso con 4 componentes (idealmente, debería estar próximo a 1). Esto sugiere que la calidad del ajuste varía mucho dependiendo del juez.

Los R²Y y R²X acumulados que corresponden a las correlaciones entre las variables explicativas (X) y las variables dependientes (Y) con los componentes son muy próximas a 1 considerando 4 componentes. Esto indica que los 4 componentes generados por la regresión de mínimos cuadrados parciales resumen bien tanto las Xs como las Ys.

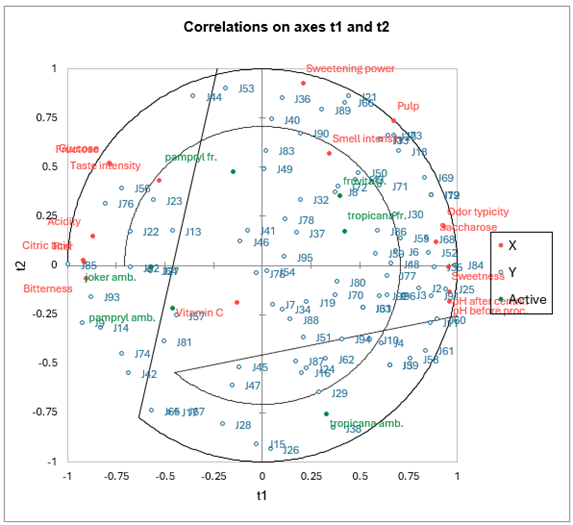
El primer mapa de correlaciones permite visualizar, sobre los primeros dos componentes, las correlaciones entre las Xs y los componentes, y las Ys y los componentes.

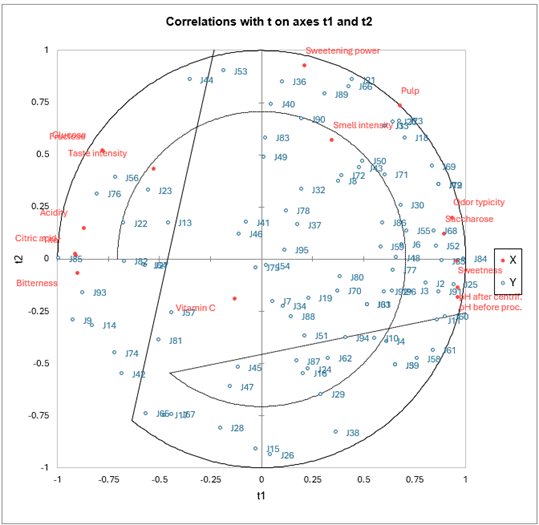
Podemos ver que para algunos jueces que se muestran en el centro del mapa, las correlaciones son bajas. Al observar la tabla correspondiente, vemos que, por ejemplo, el juez J54 solo correlaciona con el cuarto componente, que está globalmente poco correlacionado con las variables explicativas.

En lo que concierne a las variables explicativas, nos damos cuenta de que la vitamina C no está bien representada en las dos primeras dimensiones. Podemos interpretar esto como el hecho de que esta variable solo explica pequeñas preferencias de los jueces, lo cual no es sorprendente, ya que no tiene un fuerte efecto en el sabor o en otros criterios que podrían influir fácilmente sobre la preferencia de los jueces. Nos damos cuenta de las fuertes correlaciones entre la fructosa y la glucosa, entre los dos pH, y la correlación negativa entre el pH y la acidez y el titer. También hay que notar cuán diferentes son los jueces: no se concentran en una parte del círculo de correlaciones, sino que se distribuyen a su alrededor.

El mapa que muestra las variables dependientes en los vectores c, y las variables explicativas en los vectores w*, permite visualizar la relación global entre las variables. Los w* están relacionadas con los pesos de las variables en los modelos.

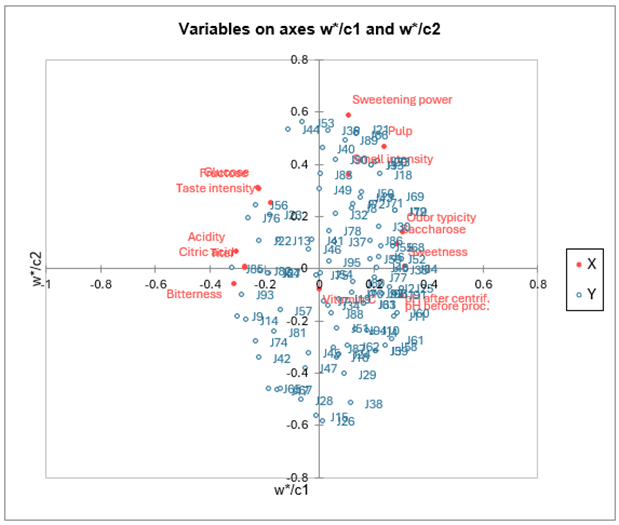
Si proyectamos una variable explicativa sobre el vector de una variable dependiente (los vectores solo se muestran si hay menos de 50 variables dependientes) podemos hacernos una idea de la influencia de la variable explicativa en el modelado de la variable dependiente.

Las coordenadas de los zumos de naranja en el espacio de las t coordenadas están disponibles en una tabla y se muestran en un mapa. Nos damos cuenta de que los productos están bien diferenciados.

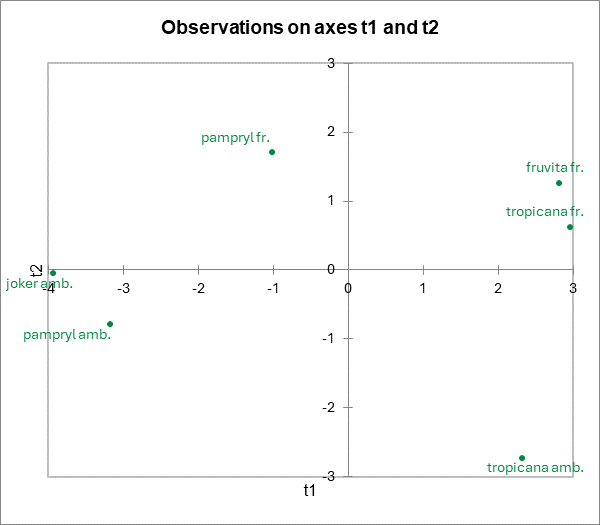
Un nuevo mapa de correlaciones permite superponer los productos sobre el mapa de correlaciones anterior. En la leyenda reemplazamos “Obs” por “Juices”, modificando el nombre de la serie en la barra de herramientas de Excel, después seleccionamos la serie haciendo clic en uno de los puntos. Como casi siempre con XLSTAT, los gráficos son gráficos de Excel y pueden modificarse con facilidad.

En su artículo, Tenenhaus et al. interpretan esta tabla en detalle. Deducen de ella la existencia de 4 grupos o clusters de jueces bien identificados. Estos autores aconsejan volver a ejecutar regresión de mínimos cuadrados parciales sobre cada uno de estos grupos. De esta manera obtienen mejores valores Q² y R². Para el primer grupo, el R²Y es de 0.63 en lugar del 0.53 obtuvimos con todos los jueces.

A continuación se muestran dos tablas que contienen los resultados de los componentes u y u~. Un gráfico permite visualizar las observaciones (en nuestro caso, los zumos) en el espacio de u~.

Las siguientes tablas permiten visualizar para cada variable dependiente los índices Q² y Q² acumulado como función del número de componentes. Notamos que para varias variables se obtiene el máximo en el índice Q² acumulado solo para uno o dos componentes (por ejemplo J5, J6, J7).

Se muestra opcionalmente una serie de tablas con el coeficiente R2 para cada variable de entrada con los componentes t. La opción no está activada de forma predeterminada, y las tablas no se tienen en cuenta en este tutorial.

La siguiente tabla muestra los VIPs (importancia de la variable para la proyección, Variable Importance for the Projection) para cada variable explicativa, para un número cada vez mayor de componentes. Esto permite identificar rápidamente cuáles son las variables explicativas que contribuyen en mayor medida a los modelos. Para el modelo con un componente podemos ver que la vitamina C, el poder edulcorante, la intensidad del olor y la intensidad del gusto tienen una influencia baja en los modelos.

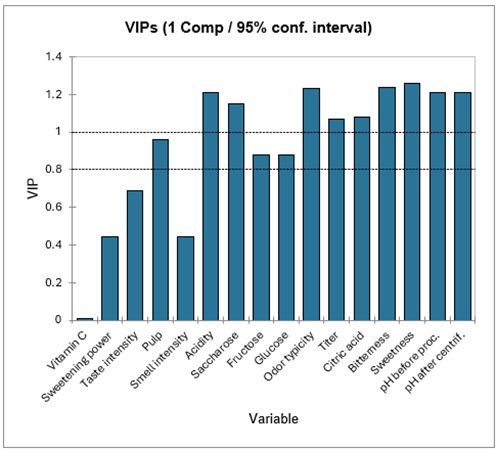
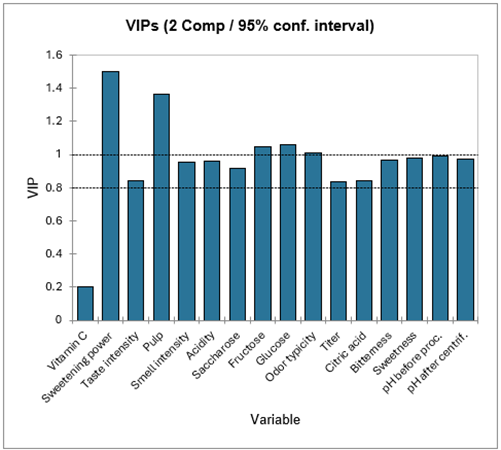
La siguiente tabla muestra los parámetros (o coeficientes) de los modelos correspondientes a cada variable dependiente. Las ecuaciones de los modelos se muestran debajo de esa tabla. Las ecuaciones se pueden volver a utilizar más adelante para fines de simulación o de predicción.

Para cada modelo, XLSTAT muestra los coeficientes de bondad del ajuste, la tabla de coeficientes estandarizados, y la tabla de las predicciones y los residuos. El análisis del modelo correspondiente al juez J1 permite llegar a la conclusión de que el modelo está bien ajustado (este coeficiente es igual a 0.88). Sin embargo, el número de grados de libertad es bajo, y podría estar enfrentándose a un problema de sobreajuste. Esto también se confirma cuando nos fijamos en los coeficientes estandarizados: los intervalos de confianza de cada coeficiente son amplios e incluyen 0. Puesto que nos dimos cuenta de que el índice Q’² acumulado correspondiente a este modelo alcanza su valor máximo con 2 componentes, es probable que un modelo con solo dos componentes fuera mejor.

Hemos llevado a cabo un nuevo análisis de regresión por mínimos cuadrados parciales, usando solo J1 como variable dependiente, y forzando el número de componentes (ver la pestaña Opciones) a 2. Los resultados se muestran en la hoja PLS2. Ahora podemos ver que la calidad de los resultados ha mejorado. La siguiente tabla corresponde a los coeficientes estandarizados del nuevo modelo.

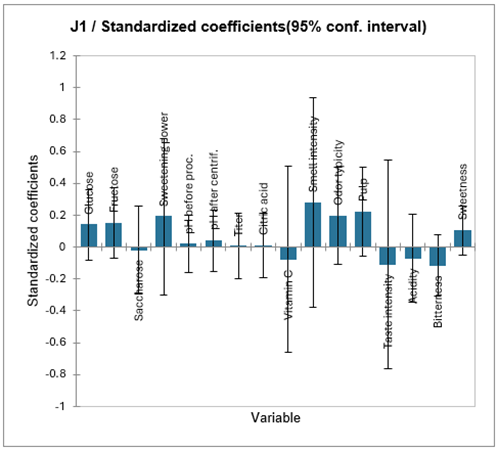
Podemos ver aquí que los coeficientes son significativamente diferentes de cero solo para “Intensidad de olor” y “Tipicidad del olor”. La tabla de predicciones y residuos permite verificar que las calificaciones otorgadas por el juez 1 están bien reproducidas por el modelo.

Por último, se muestran la tabla con DModX y DModY, así como los gráficos correspondientes que permiten identificar rápidamente los posibles valores atípicos (outliers). En nuestro caso no hay ningún valor atípico ya que todos los valores son inferiores a DCritX DCritY.

Observe por favor este vídeo para ver una demostración.