Partial Least Square (PLS) Regression in Excel

Dieses Tutorium wird Ihnen helfen, eine Partielle Kleinste Quadrate (PLS) Regression in Excel mithilfe der XLSTAT Software einzurichten und zu interpretieren.

Datensatz für die Durchführung einer Partiellen Kleinsten Quadrate Regression

Dieses Tutorial basiert auf Daten, die ausführlich in [Tenenhaus, M., Pagès, J., Ambroisine L. & Guinot, C. (2005). PLS methodology for studying relationships between hedonic judgements and product characteristics. Food Quality an Preference. 16, 4, pp 315-325] untersucht wurden. Die Daten, die in dem zugehörigen Artikel benutzt wurden, entsprechen 6 Orangensäften beschrieben von 96 Richtern.

Absicht der Partiellen Kleinsten Quadrate Regression

Die PLS-Regression wird im folgenden erlauben eine gleichzeitige Karte der Richter, den Produkteigenschaften und den Produkten zu erzeugen und darüber hinaus die Beziehung zwischen bestimmten Richtern und bestimmten Eigenschaften. Ein Excel-Blatt, das Daten und Ergebnisse enthält, die in diesem Tutorial benutzt wurden, können hier heruntergeladen werden.

Erstellen einer Partiellen Kleinsten Quadrate Regression

• Sobald XLSTAT geöffnet ist, klicken Sie auf Datenmodellierung / PLS-Regression.

• Nachdem Sie auf die Schaltfläche geklickt haben, wird das Dialogfeld zur Partial Least Squares Regression angezeigt.

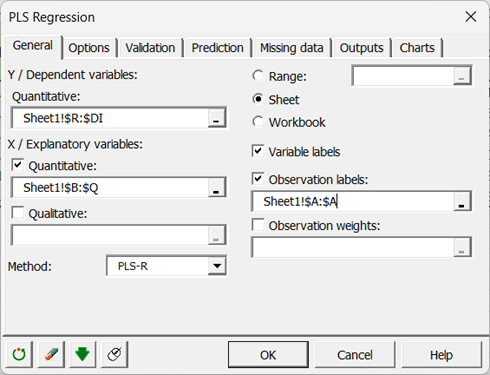
• Im Feld Abhängige Variable(n) wählen Sie mit der Maus die Bewertungen der 96 Prüfer aus.

• Die Bewertungen sind die "Ys" des Modells, da wir die Bewertungen, die von den Prüfern gegeben wurden, erklären möchten.

• Im Feld Quantitative Variable(n) wählen Sie die erklärenden Variablen aus, die in unserem Fall die physikalisch-chemischen Deskriptoren sind.

• Die Namen der Orangensäfte wurden ebenfalls als Beobachtungsbezeichnungen ausgewählt.

• Im Tab Optionen des Dialogfelds stellen wir die Anzahl der Komponenten auf 4 in den Stoppbedingungen ein.

• Zuletzt wurde im Tab Diagramme die Option Farbige Etiketten aktiviert, um das Lesen der Diagramme zu erleichtern. Die Option Vektoren wurde deaktiviert, um die Diagramme nicht zu überladen.

• Die extrem schnellen Berechnungen beginnen, wenn Sie auf OK klicken. Die Anzeige der Ergebnisse wird angehalten, um Ihnen die Auswahl der Achsen für die Karten zu ermöglichen.

• Dann müssen Sie im Achsen auswählen-Fenster nur auf Fertig klicken, damit die Diagramme nur für die ersten beiden Achsen angezeigt werden.

Interpretieren der Ergebnisse einer Partiellen Kleinsten Quadrate Regression

Nach den Tabellen der einfachen Statistiken und den Korrelationen zwischen den ausgewählten Variablen (abhängige Variablen werden in blau dargestellt und quantitative abhängige Variablen in schwartz), anschliessend werden die spezischen Ergebnisse der PLS-Regression angezeigt.

Die erste Tabelle und das zugehörige Diagramm erlauben es die Qualität der PLS-Regression in Abhängigkeit von der Anzahl der Komponenten zu beurteilen.

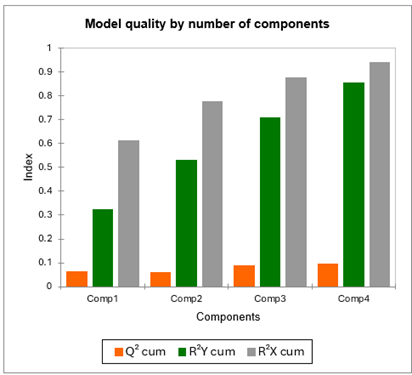
Der Q² kumuliert Index mißt die globale Anpassungsgüte and die prädiktive Qualität der 96 Modelle. XLSTAT-PLS wählte automatisch 4 Komponenten. Man sieht, dass Q² klein bleibt, auch mit 4 Komponenten (idealerweise sollte er nah bei 1 liegen).

Die unterstellt, dass die Qualität der Anpassung stark von den Richtern abhängt. Die kumulierten R²Y und R²X, die den Korrelationen zwischen den erklärenden (X) und den abhängigen (Y) Variablen mit den Komponenten entsprechen sind nahe bei 1 mit 4 Komponenten. Die bedeutet, dass die 4 von der PLS-Regression generierten Komponenten gut die Variablen der X und der Y zusammenfassen.

Die erste Korrelationenkarte erlaubt es die Korrelationen zwischen den X Variablen und den Komponenten und den Z Variablen und den Komponenten auf den Achsen der ersten beiden Komponenten anzuzeigen.

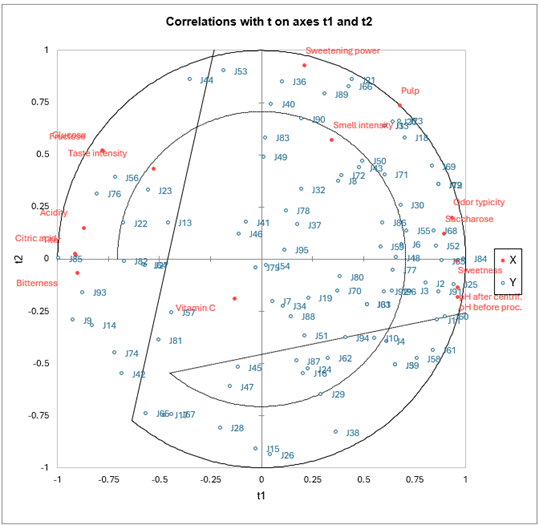
Man kann sehen, dass für einige Richter, die im Zentrum der Karte dargestellt sind, die Korrelationen klein sind. Beim Betrachten der entsprechenden Tabelle sieht man zum Beispiel für den Richter J54 ausschließlich mit der 4. Komponente korreliert, die im allgemeinen wenig mit den erklärenden Variablen korreliert. Betrachtet man die erklärenden Variablen, so bemerkt man, dass das Vitamin C nicht gut auf den ersten beiden Komponenten dargestellt wird. Man dies damit interpretieren, dass diese Variable nur wenig die Präferenzen der Richter erklärt, was nicht verwunderlich ist, da es keinen starken Einfluss auf den Geschmack oder andere Kriterien, die leicht die Präferenzen der Richter beeinflussen könnten. Wir bemerken ebenfalls die starken Korrelationen zwischen der Fruktose und der Glukose, zwischen den beiden pH-Werten, und der negativen Korrelation zwischen dem pH und dem Säuregehalt und dem Titer. Man sollte ebenfalls bemerken, wie verschieden die Richter sind: Sie sind nicht auf einen Bereich des Korrelationskreises beschränkt, sondern überall verteilt.

Die Karte, die die abhängigen Variablen auf den c Vektoren und die erklärenden Variablen auf den w* Vektoren darstellt, erlaubt es die globale Beziehung zwischen den Variablen anzuzeigen. Die w* sind abhängig von den Gewichten der Variablen in den Modellen.

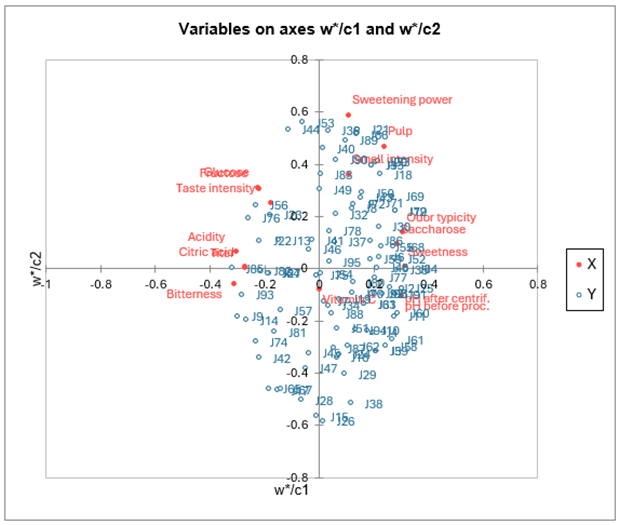
Wenn man eine erklärende Variable auf den Vektor einer abhängigen Variable projeziert, (Die Vektoren werden nur angezeigt, falls es sich um weniger als 50 abhängige Variablen handelt.) so bekommt man eine Idee über den Einfluß der erklärenden Variablen beim Modellieren der abhängigen Variablen.

Die Koordinaten der Orangensäfte im Raum der t Koordinaten werden in einer Tabelle sowie in einer Karte dargestellt. Man bemerkt, dass die Produkte wohl unterschieden sind.

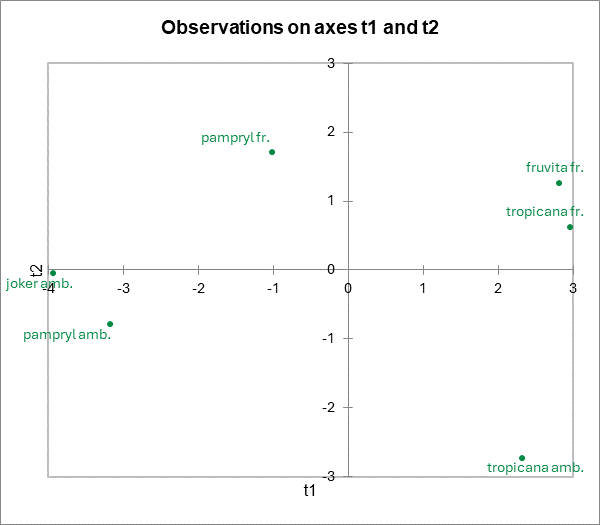
Eine weitere Korrelationskarte erlaubt es die Produkte in die vorherige Korrelationskarte einzutragen (Mittels Superpositionierung). In der Legende wurde "Beob" durch "Säfte" ersetzt, durch verändern des Seriennamens in der Excel-Toolbar, nachdem die Serie durch Klicken auf einen der dazugehörigen Punkte aktiviert wurde. Wie fast immer in XLSTAT, so ist auch dieses Diagramm ein Excel-Chart, das leicht verändert werden kann.

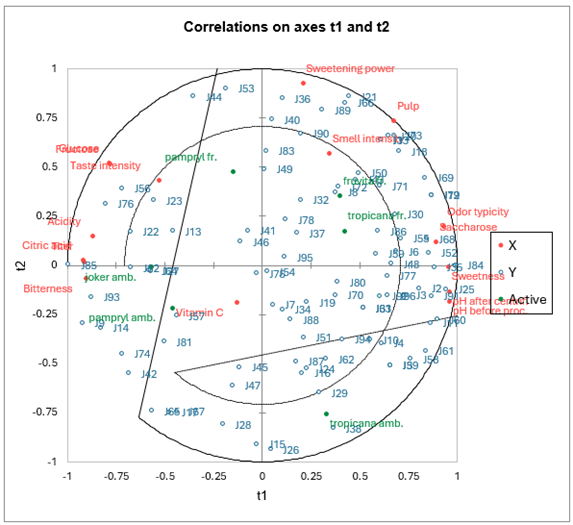
In Ihrem Artikel interpretieren Tenenhaus et al. auführlich dieses Diagramm. Sie leiten die Existenz von 4 wohldefinierten Cluster von Richter ab. Sie raten ebenfalls erneute PLS-Regressionen auf jeder dieser 4 Gruppen durchzuführen. Auf diese Art und Weise erhält man bessere Q² und R². Für die erste Gruppe beträgt R²Y 0.63 anstatt 0.53, die wir im Modell mit allen Richtern erhalten haben.

Anschließend werden zwei Tabellen mit den Ergebnissen für die u und u~ Komponenten angezeigt. Ein Diagramm erlaubt es die Beobachtungen (in unserem Fall die Orangensäfte) im Raum der u~ darzustellen.

Die folgenden Tabellen erlauben es für jede abhängige Variablen die Werte für den Q² und den kumulierte Q² Index in Abhängigkeit von der Anzahl der Komponenten anzuzeigen. Man bemerkt, dass für einige Variablen das Maximum des kumulierten Q² für eine oder nur zwei Komponenten erreicht wird (beispielsweise J5, J6, J7).

Eine Folge von Tabellen mit den Werten für R² für jede Eintrittsvariable in Bezug auf jede Komponente t wird wahlweise angezeigt. Diese Option ist nicht automatisch aktiviert, daher werden diese Tabellen in diesem Tutorial nicht behandelt.

Die folgende Tabelle enthält die VIPs (Variable Importance for the Projection) für jede jede erklärende Variable in Bezug auf jede Komponente. Die erlaubt es schnell die Variablen zu identifizieren, die am meisten zum Modell beitragen. In der ersten Komponente kann man sehen, dass das Vitamin C, die Süßkraft, die Geruchintensität und die Geschmacksintensität geringen Einfluß auf das Modell haben.

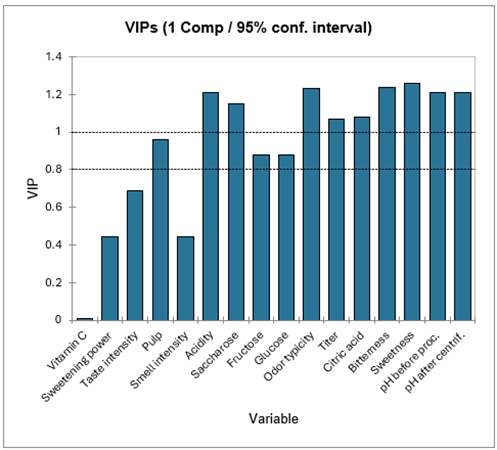
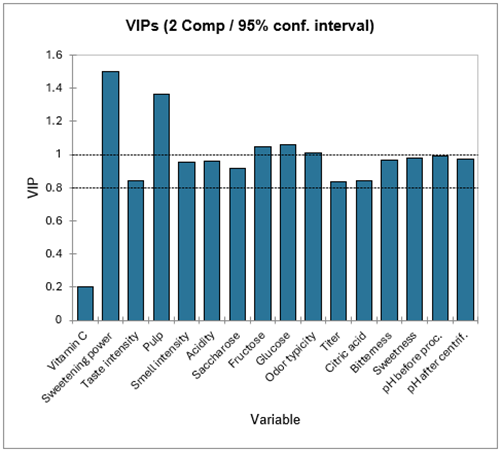
Die nächste Tabelle zeigt die Parameter (oder Koeffizienten) der zugehörigen Modelle für jede abhängige Variable an. Die Gleichungen der Modelle werden im Anschluß an die Tabelle angezeigt. Diese Gleichungen können später zur Vorhersage oder Simulation wiederverwendet werden.

Für jedes Modell zeigt XLSTAT-PLS die Anpassungsgüter der Koeffizienten an, die Tabelle der standardisierten Koeffizienten und die Tabelle der Vorhersagen und Residuen. Die Analyse des Modells, dass dem Richter J1 entspricht, erlaubt es zu schließen, das das Modell gut paßt (R² ist gleich 0.88). Jedoch ist die Anzahl der Freiheitsgrade gering und es könnte ein Overfitting Problem vorliegen. Dies wird ebenfalls bei einem Blick auf die standardisierten Koeffizienten bestätigt: Für jeden Koeffizient ist das zugehörige Konfidenzintervall recht groß und schließt den Wert 0 mitein. Da man bemerkt, dass das zugehörige kumulierte Q², das diesem Modell entspricht, sein Maximum schon bei 2 Komponenten erreicht, ist es wahrscheinlich besser im Modell nur 2 Komponenten zu berücksichtigen.

Wir haben eine weitere PLS-Analyse durchgeführt, mit lediglich J1 als abhängiger Variablen und mit einer festegesetzten Anzahl 2 an Komponenten (siehe Reiter Optionen). Die Ergebnisse werden auf dem PLS2 Blatt angezeigt. Mann kann nun feststellen, dass sich die Qualität der Ergebnisse verbessert hat. Das folgende Diagramm entspricht den standardisierten Koeffizienten des neuen Modells.

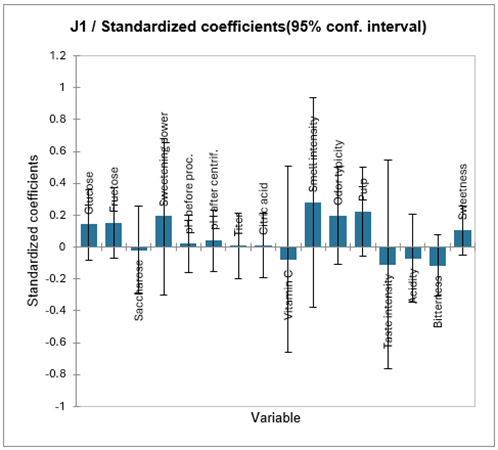
Man kann sehen, dass für alle Variablen außer für den pH, die Koeffizienten signifikant von 0 verschieden sind. Jedoch sind die Geruchsintensität, der Fruchtgehalt, die Süßkraft und die Eigenheit die einflußstärksten Variablen des Modells. Die Tabelle der Vorhersagen und Residuen erlauben es zu überprüfen, ob die Noten, die von Richter 1 vergeben wurden auch durch das Modell reproduziert werden.

Zuletzt werden mit der Tabelle der DModX und DModY und den dazugehörigen Diagrammen Informationen zum raschen Auffinden von Ausreißern gegeben. In unseren Fall gibt es keine Ausreißer, da alle Werte kleiner als DCritX oder DCritY sind.