Régression Ridge dans Excel
Ce tutoriel explique comment mettre en place et interpréter une régression Ridge dans Excel en utilisant le logiciel de statistiques XLSTAT.
Jeu de données pour réaliser une régression Ridge
Les données originales sont dues à Osborne et al. (1984). Le jeu de données contient, pour 30 cookies, les discrétisations de spectres en proche infra-rouge. Le spectre est observé sur toutes les longueurs d’ondes comprises entre 1100 et 2460 nanomètres, avec un espacement de 40 nanomètres entre chaque longueur d’onde, ce qui fait donc 35 variables explicatives dans le jeu de données. Le tableau de données contient, également, la composition en eau de chacun des cookies.
But de ce tutoriel
Le but de ce tutoriel est d’apprendre à mettre en place et interpréter une régression Ridge afin de prédire la composition des différents cookies en eau.
Paramétrer la régression Ridge
Une fois XLSTAT lancé, cliquez sur Modélisation des données/ Régression Ridge comme indiqué ci-dessous :
Une fois que vous avez cliqué sur le bouton, la boîte de dialogue de la régression Ridge apparaît.
Vous pouvez alors sélectionner les données sur la feuille Excel. La Variable dépendante correspond à la variable expliquée (ou variable à modéliser), qui est dans ce cas précis la composition en eau des cookies.
Les Variables quantitatives explicatives correspondent à toutes les colonnes numérotées de L1 à L35. On veut ici expliquer la variabilité de la contenance en eau dans les cookies en fonction du spectre.
On ne sélectionne que les 20 premiers cookies du jeu de données pour participer à la modélisation, les autres serviront à la prédiction.
Comme le nom de chaque variable est présent au début du fichier, assurez-vous que la case Libellés des variables est cochée.
Vous pouvez, également, cocher la case Libellés des observations et sélectionner le nom des différents cookies.
Dans l'onglet Options, on utilise la validation croisée pour trouver le paramètre de régularisation lambda optimal. On choisit de former 5 blocs pour la validation croisée et de tester 100 valeurs de lambda.
Dans l’onglet Prédiction, sélectionnez les données sur lesquelles vous souhaitez obtenir une prédiction. On sélectionne, ici, les 10 derniers cookies composant le jeu de données.
Dans l’onglet Sorties, sélectionnez les sorties comme indiqué ci-dessous :
Dans l’onglet Graphiques, vous pouvez activer l’option Evolution de la MCE (Validation croisée) qui permet d’avoir accès à l’évolution de la MCE (Moyenne des Carrés des Erreurs) en fonction du paramètre de régularisation.
Les calculs démarrent lorsque vous cliquez sur OK. Les résultats sont ensuite affichés.
Interpréter les résultats d’une régression Ridge
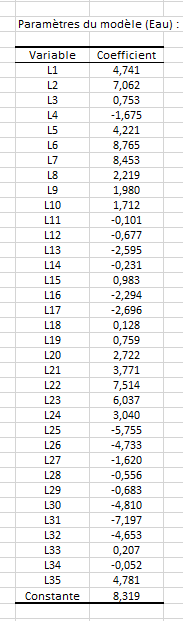
Le tableau « Paramètres du modèle » fournit les détails sur le modèle et est essentiel dès lors que le modèle doit être utilisé pour faire des prévisions ou pour analyser l’importance des variables. Nous voyons que les 35 variables ont été conservées dans la modélisation avec des coefficients de faible valeur et relativement homogènes.
Le graphique suivant affiche l’évolution de la MCE en fonction du paramètre de régularisation Lambda. La valeur de Lambda sélectionnée par XLSTAT est celle qui minimise la MCE, soit ici environ 0,133.
Le dernier tableau donne, suite à l’estimation du modèle, les prédictions de la composition en eau des 10 cookies composant le jeu de données de prédiction.
Conclusion sur la régression Ridge
Finalement, contrairement à la régression LASSO, la régression Ridge a modélisé la composition en eau des différents cookies avec la totalité des 35 variables à disposition. En parallèle, à l’inverse de la régression LASSO, aucune variable ne se démarque réellement par un gros coefficient dans la modélisation construite par la régression Ridge.
Cet article vous a t-il été utile ?
- Oui
- Non