ARIMA Modelle in Zeitreihen einfügen - Anleitung

Dieses Tutorium zeigt Ihnen, wie Sie ein ARIMA - Autoregressive Integrated Moving Average - Modell in Excel mithilfe der Software XLSTAT einrichten und interpretieren.

Datensatz zur Anpassung eines ARIMA-Modells an eine Zeitreihe

Wir stellen im Diagramm einen globalen Aufwärtstrend fest, dass jedes Jahr ein ähnlicher Zyklus beginnt, und dass die Variabilität innerhalb eines Jahres im Laufe der Zeit anscheinend zunimmt. Bevor wir das ARIMA-Modell anpassen, müssen wir die Variabilität stabilisieren. Hierzu transformieren wir die Reihe mithilft einer Log-Transformation. Wir können im nachstehenden Diagramm sehen, dass die Variabilität reduziert ist.

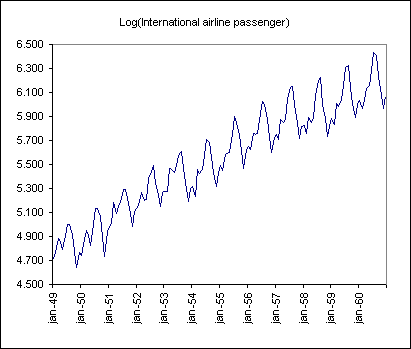
Wir können jetzt ein ARIMA(0,1, 1)(0,1,1)12-Modell anpassen, das dafür geeignet zu sein scheint, den Trendeffekt und die jährliche Saisonalität der Daten zu entfernen.

Einrichten der Anpassung eines ARIMA-Modells an eine Zeitreihe

Nach dem Öffnen von XLSTAT wählen Sie den Befehl XLSTAT/Zeitreihenanalyse/ARIMA.

Nach dem Klicken des entsprechenden Buttons erscheint das Dialogfenster ARIMA. Markieren Sie die Daten in dem Excel-Tabellenblatt. Im Feld Zeitreihen können Sie jetzt die Log(Passagier)-Daten auswählen.

Die Option Zentrieren wird aktiviert gelassen, da wir möchten, dass XLSTAT die Reihe vor der Optimierung des ARIMA-Models automatisch zentriert.

Nachdem Sie die Daten ausgewählt haben, definieren Sie den Typ des ARIMA-Modells durch Eingabe des Werts der Ordnung (p,d,q)(P,D,Q)s. Die Periode der Serien wird auf 12 gesetzt, da sich die Zyklen anscheinend jedes Jahr (12 Monate) wiederholen.

Die Option Beschriftung der Serien wird aktiviert, da die erste Zeile der ausgewählten Daten den Kopf der Variable enthält.

Geben Sie in die Registerkarte Validierung 12 ein, sodass die letzten 12 Werte nicht zur Anpassung des Modells sondern nur zur Validierung des Modells verwendet werden.

Die Berechnungen beginnen, sobald Sie auf OK geklickt haben. Die Ergebnisse werden dann angezeigt.

Interpretieren der Ergebnisse einer ARIMA-Modellanpassung an eine Zeitreihe

Nach den zusammenfassenden Statistiken der Reihe zeigt eine Tabelle die verschiedenen Kriterien an, die die Evaluierung der Qualität der Anpassung und den Vergleich der Anpassung dieses Modells mit anderen Modellen (falls verfügbar) ermöglicht.

Die nächste Tabelle zeigt die Parameter des Modells an. Wir stellen fest, dass sich sowohl der Parameter MA(1) als auch SMA(1) erheblich von 0 unterscheiden, da das Konfidenzintervall von 95 % 0 nicht einschließt. Die Konfidenzintervalle werden mithilfe der Hessenmatrix nach der Optimierung, was andere Softwareprodukte normalerweise anzeigen, und mithilfe einer asymptotischen Methode berechnet. Die Konstante des Modells ist fest, da sie aus dem Entfernen des Mittelwerts resultiert.

Das ARIMA-Modell sieht folgendermaßen aus:

Y(t) = 0,000+Z(t-1)-0,348.Z(t-1)-0,562.Z(t-12)+0,195*Z(t-13), wobei Z(t) ein weißes Rauschen N(0, 0.001) Y(t)=(1-B)(1-B12)X(t) und X(t) die Eingangsreihe ist.

Die Prognosegleichung für die X(t)-Reihe ist gegeben durch: X(t+1) = Y(t+1)+X(t)+X(t-11)-X(t-12)

Eine Tabelle zeigt die Werte der ursprünglichen Reihe und der geglätteten Reihe (die Vorhersagen) an. Aufgrund der Beschränkungen des Modells sind keine Vorhersagen für die ersten 13 Beobachtungen verfügbar (die Vorhersagen werden durch die Werte der Eingangsreihe ersetzt). Beachten Sie, dass eine Zeitvariable „T“ zur Vereinfachung der grafischen Darstellung erstellt wurde. Für die letzten 12 Beobachtungen wurden Vorhersagen im Validierungsmodus berechnet, und ein Konfidenzbereich steht zur Verfügung. Wir stellen fest, dass fast alle Residuen (in Rot) negativ sind. Das bedeutet, dass bei einem Vorhersagemodell das Modell den Verkehr überschätzt.

Im nachstehenden Diagramm können wir sehen, dass die Vorhersagen (Validierung) sehr nahe an den Daten liegen.