Kointegrationstest für Zeitreihen in Excel
Dieses Tutorium zeigt Ihnen, wie Sie Kointegrationstests in Excel mithilfe der Statistiksoftware XLSTAT einrichten und interpretieren.
Datensatz für die Durchführung eines Kointegrationstests
-Dem Monatsdurchschnitt des Devisenterminkurses mit einer Laufzeit von 12 Monate von US$ zu Sterling, mit Namen XUMADSY, -Dem Monatsdurchschnitt des Devisenkassakurses von US$ zu Sterling, mit Namen XUMAUSS. Beide Reihen decken einen Zeitraum von Januar 1979 bis Dezember 1999 ab.Absicht dieses Tutoriums
Der Devisenkurs drückt den Preis einer Währung, der Fremdwährung, in Bezug auf eine andere, die Eigenwährung, aus. In unserem Tutorium werden wir den Devisenterminkurs mit einer Laufzeit von 12 Monaten und den Devisenkassakurs des US Dollar gegenüber dem Britischen Pfund über den Zeitraum 1979-1999 betrachten. Einerseits ist der Devisenterminkurs mit einer Laufzeit von 12 Monaten eine Wechselkursabsicherung, bei der zwei Parteien zum gegenwärtigen Zeitpunkt den Kurs vereinbaren, zu dem sie die beiden Währungen in Zukunft (12 Monate im Voraus) wechseln werden. Andererseits legt der Devisenkassakurs den aktuellen relativen Wert der beiden Währungen fest. Im Kontext der Covered Interest Parity (CIP) wird erwartet, dass der Log des Devisenterminkurses und des Devisenkassakurses in Beziehung zu dem Differenzial zwischen inländischen und ausländischen Zinssätzen durch die folgende Relation steht: lnForward - lnSpot = rDiff. wobei InForward der Log des Devisenterminkurses, lnSpot der Log des Devisenkassakurses und rDiff das Zinssatz-Differenzial ist. Unter der Annahme effizienter Finanzmärkte sollte eine Situation risikofreier Gewinne, in der jemand einen Betrag in einer Fremdwährung leihen, zu risikofreien Sätzen in dieser Währung investieren und ihren Verkaufspreis in der Inlandswährung in einem Terminverkauf arretieren könnte, nicht möglich sein. Als Konsequenz wird das Zinssatz-Differenzial erwartungsgemäß bei I(0) liegen (oder stationär sein). Da es in der internationalen Finanzliteratur im Allgemeinen anerkannt ist, dass sowohl der Devisenkassakurs als auch der Devisenterminkurs einfach integriert sind (notiert oder I(1)), sollte eine Kointegrationsbeziehung zwischen dem Log Devisenkassakurs und Terminkurs für die oben genannte CIP-Beziehung bestehen. Im folgenden Tutorium müssen wir zuerst unsere Zeitreihen transformieren und ihren Status I(1) testen. Dann müssen wir mithilfe eines Kointegrationstests nach dem Johansen-Ansatz bewerten, dass diese beiden I(1) Prozesse zu einem I(0) Prozess kombiniert werden können, oder anders gesagt, dass die beiden Zeitreihen kointegriert sind.
Transformation von Zeitreihen
Zuerst müssen wir die aus der Datenbank der Bank of England extrahierten Reihen transformieren, um ihre Log-Werte zu erhalten. Nach dem Öffnen von XLSTAT wählen Sie Zeit/Zeitreihen Transformation (siehe unten).
 Das Dialogfenster Zeitreihen Transformation erscheint wie unten angezeigt. Wählen Sie die Zeitreihen im Excel-Tabellenblatt aus.
Die Option Beschriftung der Serien wird aktiviert, da die erste Zeile der ausgewählten Daten den Kopf der Variablen enthält.
Das Dialogfenster Zeitreihen Transformation erscheint wie unten angezeigt. Wählen Sie die Zeitreihen im Excel-Tabellenblatt aus.
Die Option Beschriftung der Serien wird aktiviert, da die erste Zeile der ausgewählten Daten den Kopf der Variablen enthält.
 In der Registerkarte Optionen wählen Sie die Box-Cox Transformation und legen Sie den Lambdawert auf 0 fest, um eine Log-Transformation auf die Serie anzuwenden:
In der Registerkarte Optionen wählen Sie die Box-Cox Transformation und legen Sie den Lambdawert auf 0 fest, um eine Log-Transformation auf die Serie anzuwenden:
 Sobald Sie auf den Button OK geklickt haben, werden die Berechnungen ausgeführt und die beiden transformierten Reihen in einem neuen Tabellenblatt angezeigt.
Zuerst der Devisenterminkurs über 12 Monate (XUMADSY) und seine Log-Transformation (Box-Cox(XUMADSY)):
Sobald Sie auf den Button OK geklickt haben, werden die Berechnungen ausgeführt und die beiden transformierten Reihen in einem neuen Tabellenblatt angezeigt.
Zuerst der Devisenterminkurs über 12 Monate (XUMADSY) und seine Log-Transformation (Box-Cox(XUMADSY)):
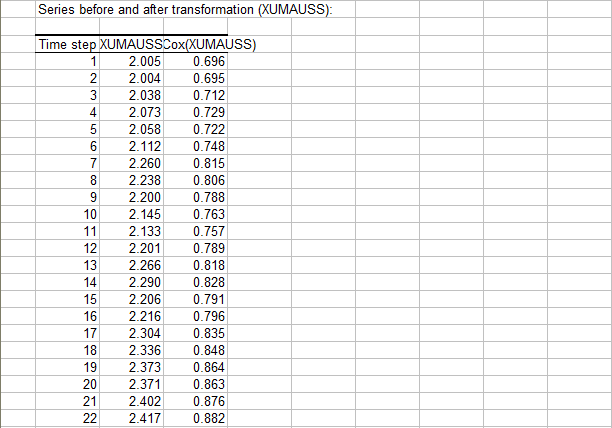
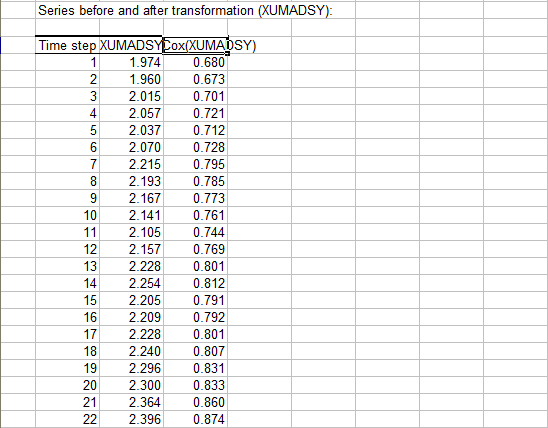 Gefolgt vom Devisenkassakurs (XUMAUSS) und seiner Log-Transformation (Box-Cox(XUMAUSS)):
Gefolgt vom Devisenkassakurs (XUMAUSS) und seiner Log-Transformation (Box-Cox(XUMAUSS)):
Beschreibende Analyse
Jetzt, wo unsere Zeitreihen bereit sind, müssen wir eine beschreibende Analyse auf ihnen anwenden, um zu kontrollieren, ob sie die erwarteten Merkmale aufweisen.
Um eine beschreibende Analyse durchzuführen, klicken Sie auf Zeit/beschreibende Analyse gemäß der nachstehenden Abbildung.
 Wählen Sie die beiden transformierten Reihen, Box-Cox(XUMADSY) und Box-Cox(XUMAUSS) mithilfe der Strg-Taste zur Auswahl mehrerer Felder aus:
Wählen Sie die beiden transformierten Reihen, Box-Cox(XUMADSY) und Box-Cox(XUMAUSS) mithilfe der Strg-Taste zur Auswahl mehrerer Felder aus:
 In der Registerkarte Ausgabe stellen Sie sicher, dass die Optionen Autokorrelationen und Partielle Autokorrelationen wie nachstehend gezeigt aktiviert sind.
In der Registerkarte Ausgabe stellen Sie sicher, dass die Optionen Autokorrelationen und Partielle Autokorrelationen wie nachstehend gezeigt aktiviert sind.
 In der Registerkarte Diagramme aktivieren Sie die Optionen Autokorrelogram (ACF) und Partielles Autokorrelogram (PACF):
In der Registerkarte Diagramme aktivieren Sie die Optionen Autokorrelogram (ACF) und Partielles Autokorrelogram (PACF):
 Sobald Sie auf OK geklickt haben, werden sowohl die deskriptiven Statistiken als auch das ACF und PACF für die beiden Reihen angezeigt.
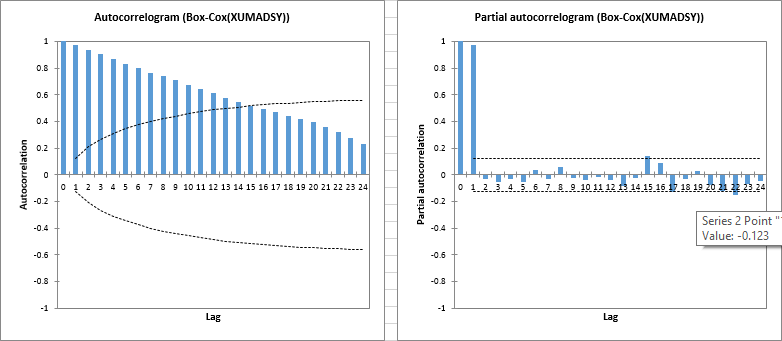
Wie die Abbildung unten zeigt, weist das ACF der Box-Cox(XUMADSY)-Reihe eine große Anzahl signifikanter Lags auf.
Beim Betrachten des PACF werden diese hohen Korrelationen scheinbar hauptsächlich durch die Lag-1-Autokorrelation erklärt, da diese als einzige im PACF stark signifikant ist.
Dieses Verhalten ist mit der erwarteten I(1) Zeitreihe weitgehend kompatibel.
Sobald Sie auf OK geklickt haben, werden sowohl die deskriptiven Statistiken als auch das ACF und PACF für die beiden Reihen angezeigt.
Wie die Abbildung unten zeigt, weist das ACF der Box-Cox(XUMADSY)-Reihe eine große Anzahl signifikanter Lags auf.
Beim Betrachten des PACF werden diese hohen Korrelationen scheinbar hauptsächlich durch die Lag-1-Autokorrelation erklärt, da diese als einzige im PACF stark signifikant ist.
Dieses Verhalten ist mit der erwarteten I(1) Zeitreihe weitgehend kompatibel.
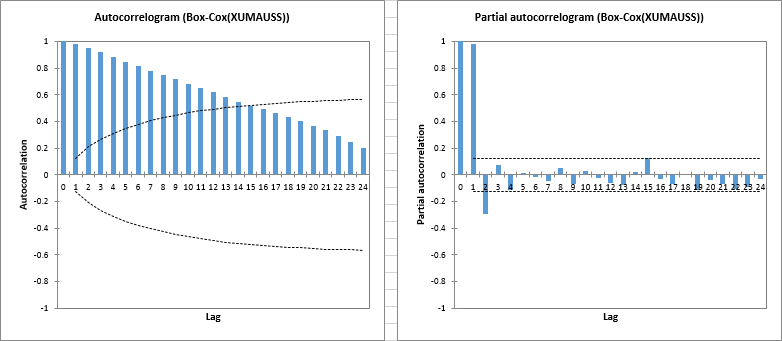
Die Simulation weist eine hohe Ähnlichkeit für die zweite Zeitreihe mit Namen Box-Cox(XUMAUSS) auf, die nachstehend mit einem stark signifikanten Lag-1 im PACF angezeigt wird.
Einheitswurzel-Tests
Nach diesen Vorprüfungen sind wir bereit, den Aspekt I(1) unserer Zeitreihe zu testen. Wir werden zwei Einheitswurzel-Tests auf unseren transformierten Zeitreihen anwenden: einen Dickey-Fuller-Test (DF) und einen Phillips-Perron-Test (PP). Wählen Sie Zeit/Einheitswurzel- und Stationaritätstests wie unten abgebildet aus.
 Wählen Sie im Feld Zeitreihen die beiden transformierten Reihen Box-Cox(XUMADSY) und Box-Cox(XUMAUSS) aus und aktivieren Sie die Dickey-Fuller- und Phillips-Perron-Tests gemäß der nachstehenden Anleitung.
In Bezug auf die Modell-Auswahl werden die Daten am besten durch das Modell mit einem Achsenabschnitt beschrieben. Sie sollten daher die Option Achsenabschnitt sowohl für den DF- als auch den PP-Test wählen.
Wählen Sie im Feld Zeitreihen die beiden transformierten Reihen Box-Cox(XUMADSY) und Box-Cox(XUMAUSS) aus und aktivieren Sie die Dickey-Fuller- und Phillips-Perron-Tests gemäß der nachstehenden Anleitung.
In Bezug auf die Modell-Auswahl werden die Daten am besten durch das Modell mit einem Achsenabschnitt beschrieben. Sie sollten daher die Option Achsenabschnitt sowohl für den DF- als auch den PP-Test wählen.
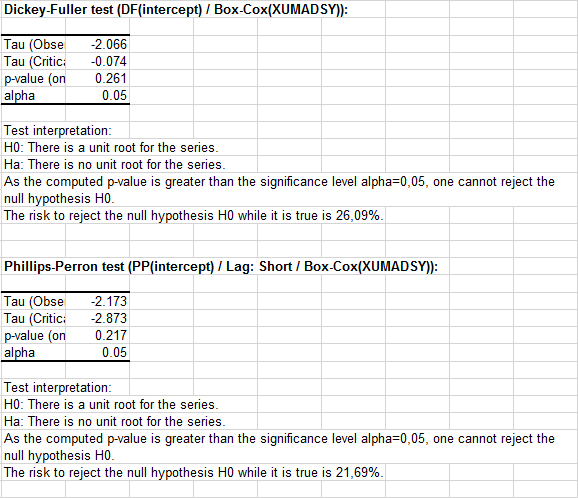
Sobald Sie auf OK geklickt haben, werden die Tests ausgeführt und die Ergebnisse werden für die beiden Reihen angezeigt. Für die Box-Cox(XUMADSY)-Reihe lehnen weder der DF- noch der PP-Test die Nullhypothese einer Präsenz einer Einheitswurzel im Datengenerierungsprozess ab (siehe unten).
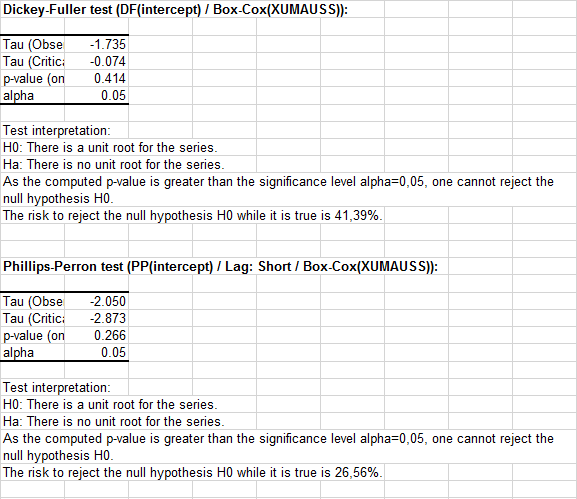
 Für die zweite Reihe ist das Konfidenzniveau, dass man die Nullhypothese nicht ablehnen sollte, sogar noch stärker:
Für die zweite Reihe ist das Konfidenzniveau, dass man die Nullhypothese nicht ablehnen sollte, sogar noch stärker:
 Um diesen Teil abzuschließen, scheint es, dass der Log des Devisenterminkurses und des Devisenkassakurses in beiden Fällen I(1) ist. Dies steht im Einklang mit dem, was von der wirtschaftlichen Theorie erwartet wird.
Wir müssen jetzt überprüfen, ob eine lineare Beziehung zwischen den beiden I(0) Reihen besteht, die eine I(0) Reihe erzeugt.
Um diesen Teil abzuschließen, scheint es, dass der Log des Devisenterminkurses und des Devisenkassakurses in beiden Fällen I(1) ist. Dies steht im Einklang mit dem, was von der wirtschaftlichen Theorie erwartet wird.
Wir müssen jetzt überprüfen, ob eine lineare Beziehung zwischen den beiden I(0) Reihen besteht, die eine I(0) Reihe erzeugt.
Einrichten eines Kointegrationstests
Zum Testen der Existenz dieser Beziehung führen wir einen Kointegrationstest nach dem Johansen-Ansatz durch. Klicken Sie auf Zeit/Kointegrationstest:
 Das Dialogfenster Kointegrationstest erscheint wie unten angezeigt. Wählen Sie zuerst zwei transformierte Zeitreihen, Box-Cox(XUMADSY) und Box-Cox(XUMAUSS). Dann müssen wir ein Modell für den Test auswählen.
Beide Reihen haben Mittelwerte, die nicht null sind, ohne Abweichung, und die Kointegrationsbeziehung, die zu Beginn dieses Tutoriums genannt wurde, wird erwartungsgemäß keinen linearen Trend haben. Daher scheint die H1*-Beschränkung für unseren Test geeignet zu sein.
Schließlich wissen wir nichts über die VAR-Order, die am besten auf unsere Gruppe von Reihen zutrifft. Wir lassen dann XLSTAT ihren Wert schätzen, indem wir die Option Automatisch wie unten gezeigt auswählen.
Das Dialogfenster Kointegrationstest erscheint wie unten angezeigt. Wählen Sie zuerst zwei transformierte Zeitreihen, Box-Cox(XUMADSY) und Box-Cox(XUMAUSS). Dann müssen wir ein Modell für den Test auswählen.
Beide Reihen haben Mittelwerte, die nicht null sind, ohne Abweichung, und die Kointegrationsbeziehung, die zu Beginn dieses Tutoriums genannt wurde, wird erwartungsgemäß keinen linearen Trend haben. Daher scheint die H1*-Beschränkung für unseren Test geeignet zu sein.
Schließlich wissen wir nichts über die VAR-Order, die am besten auf unsere Gruppe von Reihen zutrifft. Wir lassen dann XLSTAT ihren Wert schätzen, indem wir die Option Automatisch wie unten gezeigt auswählen.
 In der Registerkarte Optionen müssen wir ein Modell und ein Kriterium für die VAR-Order-Schätzung auswählen. Erneut schein ein Modell mit Achsenabschnitt angemessen, und wir verwenden das AIC-Kriterium:
In der Registerkarte Optionen müssen wir ein Modell und ein Kriterium für die VAR-Order-Schätzung auswählen. Erneut schein ein Modell mit Achsenabschnitt angemessen, und wir verwenden das AIC-Kriterium:
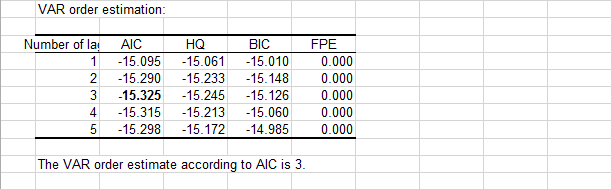
Klicken Sie auf OK und der Johansen-Kointegrationstest wird durchgeführt. In der ersten Tabelle (siehe unten) werden die Ergebnisse für die VAR-Order-Schätzung angezeigt. Der minimale AIC-Wert ergibt eine VAR-Order von 3 oder VAR(3) für unser System, d. h. eine Differenz von 2 Lags für das Vektor-Fehlerkorrekturmodell (VECM). Wir können überprüfen, ob es eine gute Übereinstimmung zwischen den vier Kriterien gibt.
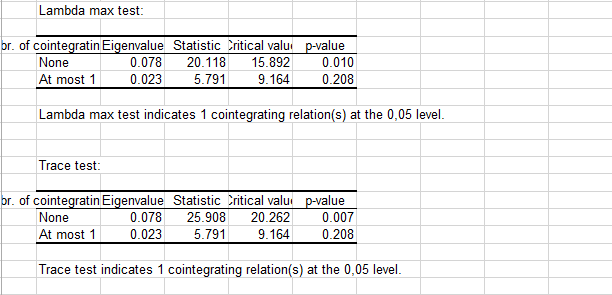
 Dann werden die Ergebnisse für beide Tests, den Maximum-Eigenwert-Test (oder Lambda-Test) und den Trace-Test angezeigt (siehe unten). Beide Tests stimmen im Rang(1) der Kointegration des Systems oder gleichermaßen in der Existenz von 1 kointegrierenden Beziehung zwischen den beiden Reihen überein. P-Werte und kritische Werte für beide Tests werden mithilfe des Oberflächenregressionsansatzes geschätzt, der bei MacKinnon-Haug-Mechelis (1998) beschrieben wird.
Dann werden die Ergebnisse für beide Tests, den Maximum-Eigenwert-Test (oder Lambda-Test) und den Trace-Test angezeigt (siehe unten). Beide Tests stimmen im Rang(1) der Kointegration des Systems oder gleichermaßen in der Existenz von 1 kointegrierenden Beziehung zwischen den beiden Reihen überein. P-Werte und kritische Werte für beide Tests werden mithilfe des Oberflächenregressionsansatzes geschätzt, der bei MacKinnon-Haug-Mechelis (1998) beschrieben wird.
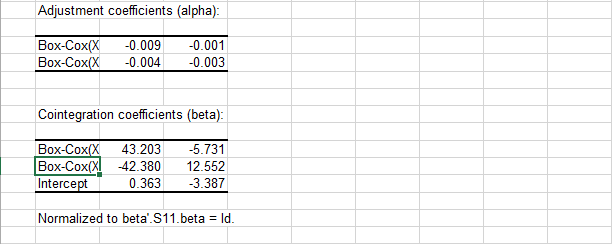
 Schließlich wird die Fakturierung der kointegrierenden Matrix in Form der Einflussmatrix (alpha) und der Kointegrations-Koeffizienten (Beta) gefolgt von der durch Johansen vorgeschlagenen Normalisierung angegeben:
Schließlich wird die Fakturierung der kointegrierenden Matrix in Form der Einflussmatrix (alpha) und der Kointegrations-Koeffizienten (Beta) gefolgt von der durch Johansen vorgeschlagenen Normalisierung angegeben:
Schlussfolgerung
Wir waren dazu in der Lage, die zwei Zeitreihen zu transformieren und nachfolgende Tests durchzuführen, um die Hypothese der beiden I(1) Reihen zu bestätigen.
Dann führten wir einen Kointegrationstest nach dem Johansen-Ansatz durch, der uns zur Schlussfolgerung führte, dass 1 Kointegrationsbeziehung zwischen den beiden Reihen existieren könnte.
Daher weist für den Zeitraum von 1979 bis 1999 der Log der Zeitreihen Devisenterminkurs für einen Zeitraum von 12 Monaten und Devisenkassakurs von US$ in Sterling eine Kointegrationsbeziehung auf wie von der Covered Interest Parity-Hypothese erwartet. Sie sollten jetzt Ihre eigene Analyse anhand eines anderen Datensatzes durchführen. Wie wäre es mit dem gleichen Datensatz aber für einen Zeitraum bis zum heutigen Tage? Die könnte zu einigen überraschenden Ergebnissen führen.
War dieser Artikel nützlich?
- Ja
- Nein