Einfache Lineare Regression in Excel - Anleitung
Dieses Tutorium wird Ihnen helfen, eine einfache lineare Regression in Excel mithilfe der XLSTAT Software einzurichten und zu interpretieren. Die einfache lineare Regression basiert auf gewöhnlichen kleinsten Quadraten (OLS). Sie sind nicht sicher, ob es sich hierbei um die Modellierungsfunktion handelt, nach der Sie suchen? Weitere Hinweise finden Sie hier.
Datensatz für die Durchführung einer linearen Regression
ie Daten stammen aus Lewis T. und Taylor L.R. (1967). Introduction to Experimental Ecology, New York: Academic Press, Inc.. Die Daten handeln von 237 Kindern, beschrieben durch ihr Geschlecht, Alter in Zoll (1 inch = 2.54 cm), und Gewicht in engl. Pfund (1 pound = 0.45 kg).Absicht dieses Tutoriums
Durch den Einsatz der einfachen linearen Regression soll ermittelt werden, wie das Gewicht der Kinder in Abhängigkeit der Größe variiert und ob ein lineares Modell sinnvoll ist. Die Methode der linearen Regression gehört zu der großen Familie der GLM (Generalized Linear Models), ebenso wie die ANCOVA und ANOVA. Dieser Datensatz wird ebenfalls in beiden Tutorials zur multiplen linearen Regression und zur ANCOVA benutzt, mit der Größe, dem Alter und dem Geschlecht als erklärenden Variablen.
Erstellen einer einfachen linearen Regression
Nach dem Öffnen von XLSTAT, wählen Sie den Befehl XLSTAT/Modellierung der Daten/Lineare Regression.

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster der linearen Regression. Sie können nun die Daten im Excel-Blatt auswählen. Es gibt mehrere Arten die Daten in den XLSTAT Dialogfenstern auszuwählen. Im untersuchten Beispiel beginnen die Daten in der ersten Zeile; es ist daher schneller die Spaltenauswahl zu benutzen. Daher erscheinen im Dialogfenster unten die Auswahlen in Form von Spalten. Die Option „Variablenbeschriftungen“ ist aktiviert, da die erste Zeile der Daten die Namen der Variablen enthält. Wählen Sie die "Abhängige Variable" (oder Modellvariable) als das Gewicht. Die quantitative erklärende Variable ist die Größe.

Die Berechnungen beginnen, sobald der Button OK geklickt wird.
Interpretieren der Ergebnisse einer einfachen linearen Regression
Falls Sie in den Optionen von XLSTAT die Option „Auswahl bestätigen lassen“ aktiviert haben, so bittet Sie XLSTAT die Anzahl der Zeilen und der Spalten der Auswahlen zu bestätigen. Die erste Tabelle zeigt die Koeffizienten der Anpassungsgüte des Modells an. Das R’² (Determinationskoeffizient) gibt den Prozentsatz der Variabilität der abhängigen Variablen an, die durch die erklärende Variable beschrieben wird. Je näher R’² bei 1 liegt, desto besser ist die Anpassung.

In diesem speziellen Fall werden 60 % der Variabilität des Gewichts durch die Größe erklärt. Der Rest der Variabilität ist auf Effekte zurückzuführen (andere erklärende Variablen), die nicht in die Analyse eingeschlossen wurden.
Es ist wichtig die Ergebnisse der Varianzanalyse-Tabelle zu untersuchen (siehe unten). Diese Ergebnisse lassen uns entscheiden, ob die erklärenden Variablen eine signifikante Information (Nullhypothese H0) in das Modell einbringen oder nicht. Mit anderen Worten ausgedrückt, ist dies eine Art zu überprüfen, ob es Sinn macht den Mittelwert zu benutzen, um die gesamte Population zu beschreiben, oder ob die Information, die von der/den erklärenden Vairable(n) eingebracht wurde, wertvoll ist.
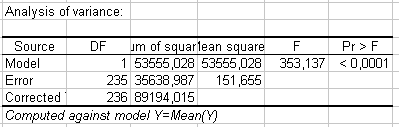
Anhand der Tatsache, dass die Wahrscheinlichkeit die dem F value entspricht kleiner als 0.0001 ist, ist das Risiko kleiner als 0.01%, dass die Annahme der Nullhypothese (kein Einfluss der erklärenden Variablen) falsch ist. Daher kann man sicher schließen, dass die drei Variablen eine signifikante Information einbringen.
Die folgende Tabelle zeigt Modelldetails an. Diese Tabelle ist hilfreich, wenn Vorhersagen benötigt werden oder wenn Sie die Koeffizienten des Modells für eine vorgegebene Population mit denen für eine andere Population vergleichen möchten. Man kann sehen, dass das 95% Konfidenzintervall des Parameters der Variable Größe sehr eng ist, wobei das Konfidenzintervall für den Achsenabschnitt Größe ist. Die Modellgleichung ist unter der Tabelle aufgeschrieben. Man stellt fest, dass der Wertebereich der Variable Größe berücksichtigt wird. Wenn die Größe um ein Zoll zunimmt, so steigt dass Gewicht um 3.8 Pfund.

Die nächste Tabelle zeigt die Residuen an. Dies ermöglicht es, jedes standardisiertes Residuum genauer zu betrachten. Diese Residuen gemäß der Annahme des linearen Regressionsmodells sollten normalverteilt sein. Dies bedeutet, dass 95% der Residuen im Intervall [-1.96, 1.96] liegen sollten. Alle Werte außerhalb des Intervalls sind potentielle Ausreißer oder lassen unterstellen, dass die Annahme der Normalität falsch ist. Wir benutzten XLSTATs DataFlagger um die Residuen außerhalb des Intervalls [-1.96, 1.96] hervorzuheben.
So kann man von den 237 9 Residuen (26, 38, 64, 69, 77) finden, die außerhalb des Bereiches [-1.96, 1.96] liegen, eine Analyse die dazu führt die Normalitätsanalyse zurückzuweisen. Eine genauere Analyse der Residuen kann im Tutorial zur ANCOVA gefunden werden.
Das erste Diagramm (siehe unten) erlaubt es die Daten, die Regressionslinie (das angepasste Modell) und die beiden Konfidenzintervalle darzustellen: Das Konfidenzintervall des Mittelwerts der Vorhersagen für eine gegebene Größe ist näher an der Linie. Das andere Konfidenzintervall einer einzelnen Vorhersage für eine gegebene Größe. Man kann klar eine lineare Tendenz ausmachen, jedoch ist eine hohe Variabilität um die Linie herum. Mann ebenfalls feststellen, dass die 9 Beobachtungen, die außerhalb des Bereichs [-1.96, 1.96] liegen, auch außerhalb des zweiten Konfidenzintervalls liegen.

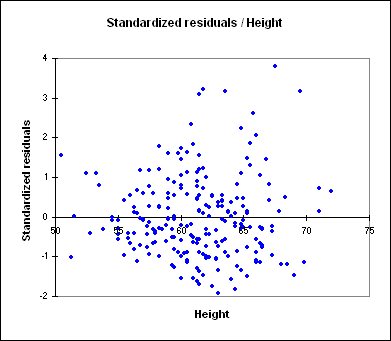
Das dritte Diagramm (siehe unten) erlaubt es die standardisierten Residuen gegenüber der Größe zu vergleichen. Hier ist es nicht der Fall, jedoch wenn in diesem Diagramm eine Tendenz festgestellt wird, so ist dass Modell nicht korrekt und eine Autokorrelation der Residuen ist anzunehmen, was gegen die Annahme einer parametrischen linearen Regression verstößt.
Das nächste Diagramm erlaubt es, die Vorhersagen der beobachteten Werte zu vergleichen. Die Grenzen des Konfidenzintervalls erlauben es, wie auf dem oben dargestellten Regressionsdiagramm, Ausreißer zu lokalisieren.

Das Histogramm der Residuen erlaubt es rasch die Residuen zu sehen, die außerhalb des Bereichs [-2, 2] liegen.

Schlussfolgerung dieser linearen Regression
Das Fazit ist, dass die Größe es erlaubt 60 % der Variabilität des Gewichts zu erklären. Ein signifikanter Anteil an Information wird nicht durch das benutzte Regressionsmodell erklärt. Im Tutorial zur Multiplen Linearen Regression wird die Variable Alter dem Modell hinzugefügt, um die Anpassungsgüte des Modells zu erhöhen.
War dieser Artikel nützlich?
- Ja
- Nein