Test F de Fisher pour comparer 2 variances dans Excel
Ce tutoriel explique comment calculer et interpréter le test F de Fisher pour comparer 2 variances avec Excel en utilisant XLSTAT.
Jeu de données pour faire un test F de Fisher pour comparer la variance de deux échantillons et but de ce tutoriel
Les données proviennent de [Fisher M. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, pp 179 -188] et correspondent à 100 fleurs d'Iris, décrites par 2 variables quantitatives (longeur des sépales, largeur des sépales). Deux espèces font partie de cette étude : setosa et versicolor.
But de ce tutoriel
Le but de ce tutoriel est de savoir si les espèces ont le même type de sépales et donc de comparer les distributions de deux échantillons.
La première chose à faire est de tester si les échantillons suivent la distribution Normale car le test de comparaison des variances de Fisher est sensible à la non-normalité des données. Les résultats sont accessibles dans le fichier Excel. Toutes les variables suivent une distribution Normale.
Nous pouvons donc lancer un test F pour tester l’égalité des variances. Si les variances sont égales, nous pourrons tenter de comparer les moyennes.
Paramétrer un test F de Fisher pour comparer la variance de deux échantillons
Pour faire un test de comparaison des variances de deux échantillons :
-
Allez dans le menu Tests paramétriques et sélectionnez l’option Comparaison des variances de deux échantillons
-
La boîte de dialogue Comparaison des variances de deux échantillons apparaît
-
Dans l’onglet Général sélectionnez les données pour les échantillons 1 et 2.
Pour l’Echantillon 1 prenez la colonne B qui contient la longueur des sépales pour la variété Versicolor et pour l’Echantillon 2 la colonne E correspondant à la la longueur des sépales pour la variété Setosa.
-
Le Format des données est Une colonne par échantillon comme chacune des colonnes correspond à un échantillon différent.
-
L’option Feuille est sélectionnée pour obtenir les résultats dans une nouvelles feuille du classeur.
-
Comme les colonnes ont un libellé dans la première cellule, l’option Libellés des colonnes est activée.
-
Nous choisissons le test F de Fisher.

-
Une fois ces paramètres choisis, passez à l’onglet Options.
-
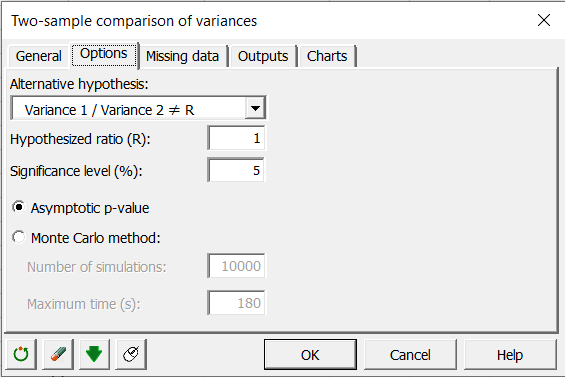
Nous souhaitons tester l’égalité des variances donc l’hypothèse alternative adéquate est : Variance 1 / Variance 2 ≠ R où R est égal à 1.
-
Le niveau de significativité par défaut est de 5%, gardez-le.
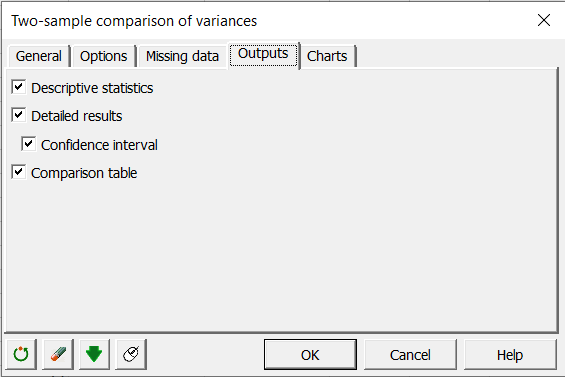
Notre jeu de données ne comporte pas de données manquantes, passez donc directement à l’onglet Sorties où vous sélectionnez Statistiques descriptives. Vous pouvez également sélectionner les autres sorties si vous le souhaitez.
Cliquez sur OK quand tout est prêt.
Interpréter les résultats d'un test F de Fisher pour comparer la variance de deux échantillons
Les résultats qui apparaissent dans une nouvelle feuille montre qu’il faut rejeter l’hypothèse H0 car la p-value est de 0,009 qui est inférieure à la limite de 0,05. Ainsi les variances ne peuvent être considérées comme étant égales. La longueur des sépales des deux populations - Versicolor et Setosa – ne suivent pas la même distribution.
Nous allons refaire le même processus pour la largeur des sépales.
Le seul changement à faire dans la procédure décrite ci-dessus est la sélection des données. Pour l’Echantillon 1 choisissez la colonne C et pour l’Echantillon 2 la colonne F.

Cette fois-ci les variances peuvent être considérées comme égales car la p-value du test (0,189) est supérieure à 0,05.

Comme l’égalité des variance est démontrée nous pouvons faire un test de comparaison des moyennes.
Comme vous pouvez le remarquer dans la table des statistiques descriptives, la moyenne de la largeur des sépales pour l’espèce Versicolor est plus petite que celle pour l’espèce Setosa. Ainsi nous allons faire un test unilatéral pour le test de comparaison des moyennes. Les tests unilatéraux sont en général plus précis.
-
Allez au menu Tests paramétriques / Tests t et z pour deux échantillons
-
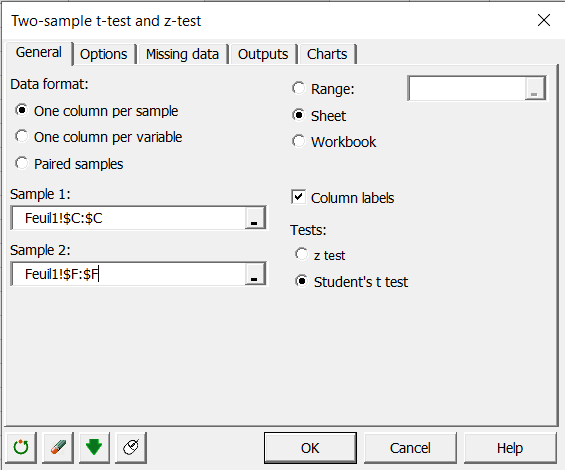
Dans l’onglet Général faites les mêmes sélections de variable que pour le test précédent
-
Sélectionnez l’option Test t de Student car nous ne connaissons pas la variance des deux populations
-
Dans l’onglet Options choisissez l’hypothèse alternative Moyenne 1 – Moyenne 2 < D où D est égal à 0.
-
Nous pouvons Supposer l’égalité des variances comme nous l’avons démontré dans le test precedent.

-
Cliquez sur OK.
D'après les résultats de ce test, nous avons démontré que les deux moyennes sont significativement différentes, la moyenne de la largeur des sépales des iris Versicolor étant plus petite que celle de la moyenne des iris Setosa. Les largeurs des sépales des deux populations - Versicolor et Setosa – suivent donc des distributions différentes.

Cet article vous a t-il été utile ?
- Oui
- Non