Comparer ≥ 2 échantillons décrits par plusieurs variables
Jeu de données pour la comparaison multidimensionnelle de k échantillons
.
Les données sont artificielles et ont été générées avec l'outil d'échantillonnage dans une distribution de XLSTAT. Les trois premières colonnes sont tirées pour les 3 groupes G1, G2, et G3 dans une loi normale standard N(0;1). Les trois suivantes sont tirées pour le premier groupe dans une Normal(2; 5) pour G1, dans une N(2.2;5.2) pour G2 et dans une N(8;7) pour G3.
Comparaison multidimensionnelle de k échantillons
Afin de montrer le fonctionnement de l'outil et la pertinence des tests, nous allons d'abord faire un test multidimensionnel sur les 3 premières colonnes, puis sur les 3 suivantes, puis sur les 6 colonnes.
1. Tests sur les trois premières colonnes
Paramétrer la comparaison de k échantillons sur les trois premières colonnes
Une fois XLSTAT lancé, choisissez la commande XLSTAT / Tests paramétriques / Tests multidimensionnels ou cliquez sur le bouton correspondant de la barre d'outils Tests paramétriques.

Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données correspondant aux trois premières colonnes sur la feuille Excel, puis la colonne B contenant les identifiants des groupes.
Interpréter les résultats de la comparaison de k échantillons sur les trois premières colonnes
Les résultats indiquent que tant pour les moyennes (test de Wilks) que pour les variances (tests de Box et de Kullback), les trois groupes peuvent être considérés comme identiques et provenant de la même population. On note avec les distances de Fisher que la distance entre G1, d'une part, et G2 ou G3 d'autre part, est plus importante que la distance entre G2 et G3, mais sans que cela soit significatif pour autant.


2. Tests sur les trois dernières colonnes
Paramétrer la comparaison de k échantillons sur les trois dernières colonnes
Les trois dernières colonnes sont sélectionnées, le reste étant inchangé.

Interpréter les résultats de la comparaison de k échantillons sur les trois premières colonnes
Dans ce cas là, les tests sur les moyennes identifient bien la différence : le test du Lambda de Wilks conclut à une différence de moyenne entre les groupes. On note que les distances de Mahalanobis ne sont significatives que lorsque le groupe 3 est concerné. Il n'est pas surprenant que la faible différence entre les 2 premiers groupes ne soient pas détectée comme significative, les échantillons étant de taille modeste.
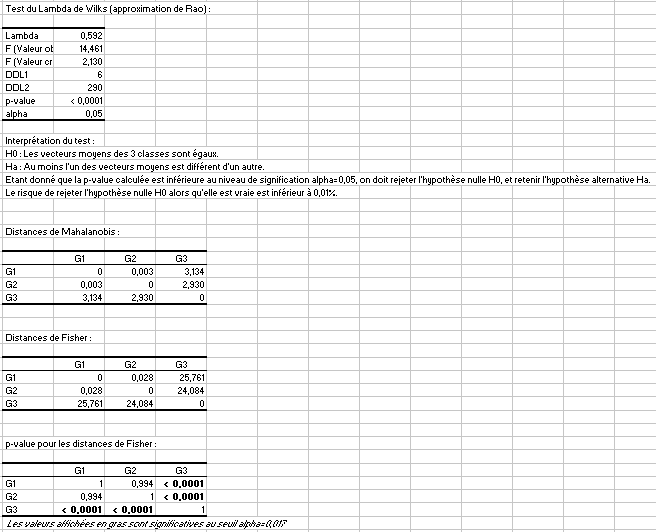
En ce qui concerne les matrices de covariance, les tests de Box sont à la limite de conclure à une différence, la p-value étant de 0.06. En revanche le test de Kullback ne parvient pas à identifier la différence. Cela s'explique par la taille de l'échantillon qui es trop faible pour bien distinguer des échantillons dont la loi a une variance de 5’² d'une loi dont la variance est 7’².

3. Tests sur les six colonnes
Paramétrer la comparaison de k échantillons sur toutes les colonnes
Cette fois ci, toutes les colonnes sont sélectionnées, et dans l'onglet "Sorties, les matrices de corrélation et covariance sont demandées.

Interpréter les résultats de la comparaison de k échantillons sur toutes les colonnes
Les tests sur les moyennes donnent des résultats très proches du cas 2. La différence entre G1 et G2 au niveau des distances de Mahalanobis est légèrement plus faible.

En revanche, les tests sur les matrices de covariance sont étonnament différents. Les petites différences observées sur les 3 premières colonnes, et celles plus importantes observées sur les 3 dernières colonnes se cumulent, avec par ailleurs des covariances non négligeables entre RV1 et RV4, entre RV2 et RV5 et entre RV3 et RV6, pour finalement donner des différences très significatives lorsque l'ont réalise les tests sur les 6 colonnes.

Cet article vous a t-il été utile ?
- Oui
- Non