Multidimensional Scaling (MDS) dans Excel

Ce tutoriel vous aidera à configurer et interpréter un Scaling Multidimensionnel (MDS) dans Excel avec le logiciel XLSTAT.

Ce guide vous permettra de choisir une méthode d'analyse multivariée appropriée en fonction de votre question et vos données.

Multidimensional Scaling

Le Multidimensional Scaling (MDS) est une méthode d'analyse de données largement utilisée dans les domaines du marketing et de la psychométrie, particulièrement dans les pays anglo-saxons. Le principe de la méthode consiste à reconstituer une carte d'individus à partir d'une matrice de proximités (similarités ou dissimilarités) entre les individus.

Dans le cas idéal où l'on dispose d'une matrice donnant les distances entre des points dans le plan (par exemple, les distances entre les villes d'une région), le Multidimensional Scaling reconstitue la carte des points, à une rotation/symétrie près.

Pour donner une configuration optimale, la méthode Multidimensional Scaling minimise un critère appelé Stress. Plus il est proche de 0, meilleure est la représentation.

Jeu de données pour réaliser un Multidimensional Scaling

Les données proviennent d'une enquête menée auprès de 10 consommateurs, auxquels on a demandé de noter (notes comprises entre 1 et 5) cinq barres chocolatées, dont un seul est sur le marché (produit P1).

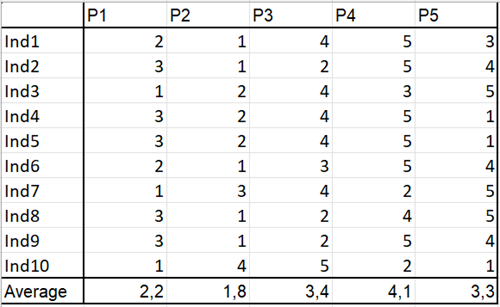
But de ce tutoriel sur le Multidimensional Scaling

Il s'agit de montrer comment les produits se positionnent sur une carte, d'après les notes données par les 10 consommateurs.

Réaliser un Multidimensional Scaling

Créer une matrice de proximité

Nous avons vu que pour utiliser le Multidimensional Scaling, nous avons besoin d'une matrice de proximité, or, nous disposons ici d'une matrice individus / produits. Pour créer une matrice de dissimilarités entre les produits, nous devons d'abord utiliser l'outil Matrices de similarité/dissimilarité de XLSTAT.

Une fois que XLSTAT est activé, cliquez sur le menu Description des données et sélectionnez Matrices de similarité/dissimilarité (voir ci-dessous).

Une fois le bouton cliqué, la boîte de dialogue apparaît.

Vous pouvez alors sélectionner les données sur la feuille Excel puis choisir les options adéquates comme il est montré ci-dessous.

Les résultats seront affichés juste en dessous du tableau des résultats (option de sortie Plage).

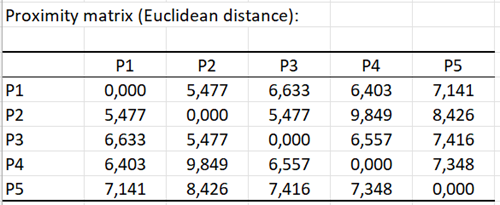
La matrice de proximité est générée par défaut et n'a pas besoin d'être spécifiée en tant que résultat spécifique. Les calculs commencent une fois que vous avez cliqué sur OK. On obtient alors la matrice des distances euclidiennes entre les produits, à partir de laquelle le Multidimensional Scaling va pouvoir être réalisé.

Paramétrer le Multidimensional Scaling

Cliquez alors sur le menu XLSTAT puis sur Analyse des données et sélectionnez Multidimensional Scaling (voir ci-dessous).

Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données sur la feuille Excel puis choisir les options adéquates comme il est montré ci-dessous. Le modèle absolu a été choisi. Ce modèle fait en sorte que les distances obtenues dans la configuration finale soient aussi proches que possible des distances euclidiennes calculées à partir des notes des consommateurs. D'autres options peuvent donner les mêmes résultats, mais avec un effet d'échelle. Par ailleurs, nous avons demandé à ce que les espaces de représentation comportent de 2 à 4 dimensions, afin d'évaluer la distorsion associée à la représentation dans un espace de faible dimension.

À moins que l'on ne donne une configuration initiale à l'algorithme, les points de départ sont choisis aléatoirement. Il est donc possible que vous obteniez un résultat légèrement différent de celui qui est affiché ici. Pour être assuré d'obtenir une solution proche de l'optimum absolu, vous pouvez augmenter le nombre de répétitions, le nombre d'itérations maximales et la précision.

Les calculs commencent lorsque vous cliquez sur le bouton OK. Après avoir choisi de représenter les graphiques sur les deux premières dimensions, les résultats s'affichent sur la feuille "MDS" du classeur Excel.

Interpréter les résultats d'un Multidimensional Scaling

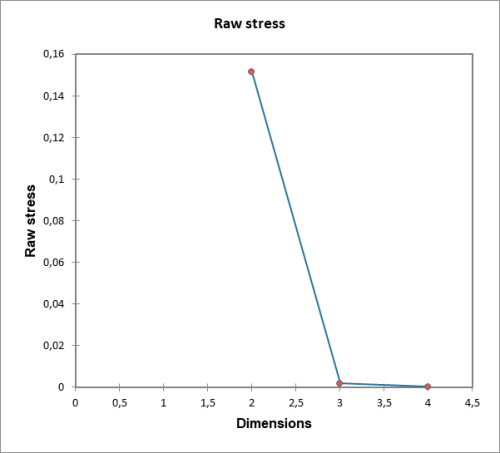
Le premier tableau montre l'évolution du stress en fonction du nombre de dimensions de l'espace de représentation. On note une rupture très nette entre les dimensions 2 et 3, et une stabilité entre les dimensions 3 et 4 (il est normal que la représentation de 5 objets soit parfaite dans un espace à 4 dimensions).

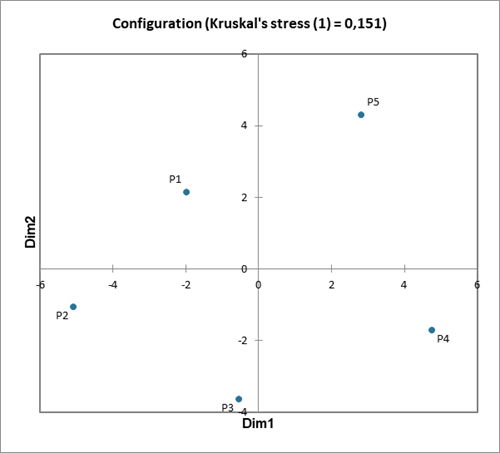
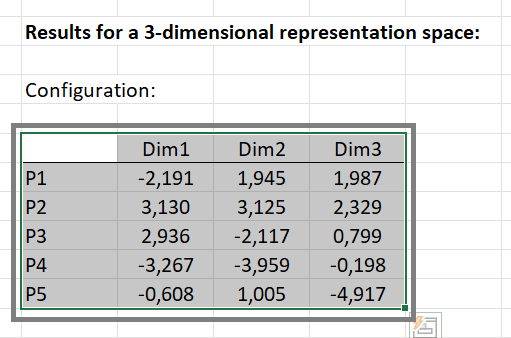
Une carte établie sur le plan Dim1 x Dim2 est produite pour l'espace à 2 dimensions.

Il est également possible de créer ces cartes pour les configurations en 3 et 4D. Cependant, cela est déconseillé. En effet, il s'agit de projections d'un nuage de points situé dans un espace à 4 dimensions sur des plans, et nous ne savons pas a priori si une de ces projections permet de représenter fidèlement les relations de proximité entre les points du nuage. Seule une ACP calculée à partir du résultat du MDS permettrait de construire une carte rendant compte le plus fidèlement possible du nuage de points.

Afin d'avoir une représentation d'une qualité supérieure, et d'éviter une mauvaise interprétation des données, nous utilisons XLSTAT-3DPlot pour représenter la configuration en trois dimensions. Pour cela, il suffit de sélectionner les données :

Puis de cliquer sur l'icône de XLSTAT-3DPlot dans la barre d'outils Visualisation des données :

On obtient alors le résultat suivant :

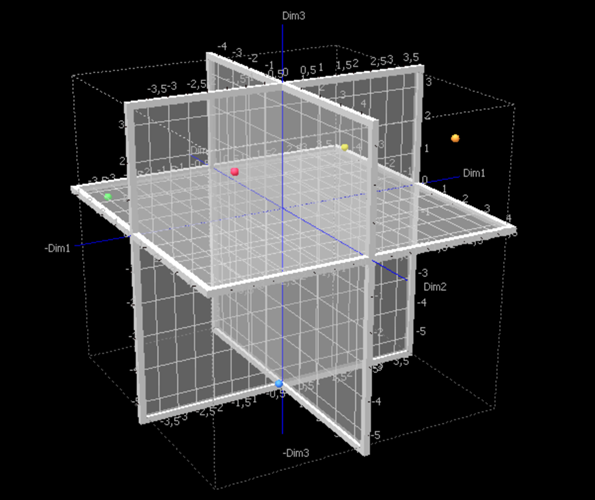
Il apparaît ainsi que les consommateurs ont collectivement bien distingué l'ensemble des produits les uns des autres puisque les produits sont dispersés. Nous savons que le produit P2 contient plus de chocolat que le produit P4 qui est celui qui en contient le moins : ils apparaissent diamétralement opposés sur le graphique à 3 dimensions. Nous voyons que les consommateurs ont sensiblement favorisé le produit P2 dans leur notation. Nous voyons aussi d'après les figures ci-dessus que les produits P3 et P5, bien qu'ayant des notes moyennes très proches, ne sont pas proches dans l'espace de représentation. Les avis entre les consommateurs sont en effet parfois opposés sur les produits P3 et P5. Cela s'explique par un goût d'arachide dû à la présence de cacahuètes dans le produit P3, apprécié par certains consommateurs et pas par d'autres.

La méthode MDS permet donc de cartographier des produits jugés par des consommateurs, l'interprétation qui en découle pouvant être beaucoup plus riche qu'une analyse à partir de statistiques simples.

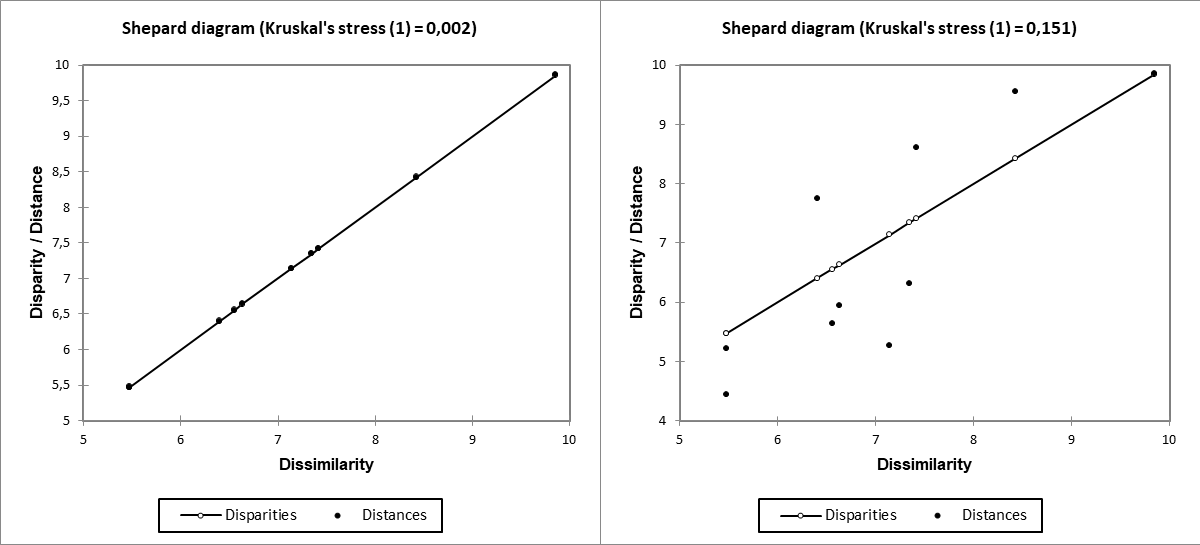
Remarque : il n'existe pas de méthode statistique rigoureuse pour évaluer la qualité et la fiabilité d'une représentation issue d'un MDS. Néanmoins, l'observation du diagramme de Shepard permet d'avoir une idée générale de la qualité de la représentation. Le diagramme de Shepard correspond à un nuage de points, dont les abscisses sont les dissimilarités observées, et les ordonnées, les distances dans la configuration issue du MDS. Plus les points sont dispersés, moins le graphique est fiable. Si la relation d'ordre au niveau des abscisses est respectée au niveau des ordonnées, le graphique est très fiable. Si les points sont alignés sur une droite, la représentation est parfaite. Le graphique de gauche correspond, pour les données de cet exemple, à la représentation dans un espace à 4 dimensions, et celui de droite correspond à la représentation dans un espace à 2 dimensions. On note une différence sensible dans la dispersion des points entre les deux graphiques.

Dans le cas du modèle absolu, les disparités sont identiques aux dissimilarités et leur représentation sur le diagramme de Shepard est donc confondue avec la ligne pour le diagramme correspondant aux 2 dimensions et avec les points des distances pour le diagramme correspondant aux 4 dimensions.

La vidéo suivante aborde le Multidimensional Scaling avec une illustration sur XLSTAT :