Analyse en Composantes Principales (ACP) avec Excel
Ce tutoriel vous aidera à configurer et interpréter une Analyse en Composantes Principales (ACP) dans Excel avec le logiciel XLSTAT.
Jeu de données pour réaliser une Analyse en Composantes Principales
Les données proviennent du US Census Bureau. Elles correspondent à la mesure de paramètres démographiques dans 51 Etats des Etats-Unis en 2000 et 2001. Dans le cadre de ce tutoriel, seules les données de l'année 2001 ont été conservées, et afin de supprimer les effets d'échelle, les variables initiales ont été converties en taux pour 1000 habitants.
But de ce tutoriel
Le but est ici d'analyser les corrélations entre les variables et d'identifier des états se différenciant fortement des autres.
Paramétrer une Analyse en Composantes Principales
-
Ouvrir XLSTAT
-
Choisir XLSTAT / Analyse de données / Analyse en Composantes Principales. Une fois le bouton cliqué, la boîte de dialogue correspondant à l'ACP apparaît.
-
Sélectionner les données sur la feuille Excel.
-
Cocher l'option Libellés des variables, car la première ligne de données contient le nom des variables.
-
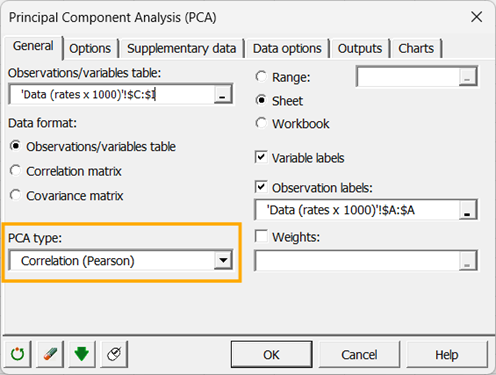
Sélectionner Observations/Variables dans le champ Format des données.
-
Sélectionner Corrélation dans le champ Type d'ACP. Cela signifie que les calculs seront basés sur une matrice composée des coefficients de corrélation de Pearson, le coefficient de Pearson étant le coefficient de corrélation classiquement utilisé. Les matrices de covariance allouent plus de poids aux variables ayant des variances élevées. Les corrélations de Spearman peuvent être plus appropriées lorsque l’ACP est exécutée sur des variables aux distributions différentes. Les corrélations polychoriques sont adaptées aux variables ordinales.
-
Dans l'onglet Sorties, activer l'option Tester la significativité pour afficher en gras les corrélations significativement différentes de 0.
-
Dans l'onglet Graphiques, activer toutes les options d'Etiquettes afin que les libellés des variables et des observations soient bien affichés et désactiver l'option Filtrer afin d'afficher toutes les observations.
-
Cliquer sur OK pour lancer les calculs.
-
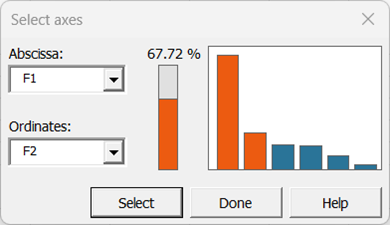
Confirmez les axes pour lesquels vous souhaitez afficher des graphiques. Dans cet exemple, 67,72 % de la variabilité est représentée par les deux premiers facteurs, mais il peut être utile de sélectionner d'autres combinaisons d'axes pour compléter et affiner l'analyse, le cas échéant.
Interpréter les résultats de l'Analyse en Composantes Principales
Qu'est ce que l'analyse en Composantes Principales ?
L'Analyse en Composantes Principales (ACP) est une méthode très efficace pour l'analyse de données quantitatives (continues ou discrètes) se présentant sous la forme de tableaux à M observations / N variables. Elle permet de :
-
visualiser et analyser rapidement les corrélations entre les N variables,
-
visualiser et analyser les M observations initialement décrites par N variables sur un graphique à deux ou trois dimensions, construit de manière à ce que la dispersion entre les données soit aussi bien préservée que possible,
-
construire un ensemble de P facteurs non corrélés
Les limites de l'Analyse en Composantes Principales viennent du fait que c'est une méthode de projection, et que la perte d'information induite par la projection peut entraîner des interprétations erronées. Des astuces permettent cependant d'éviter ces inconvénients.
Il est également important de noter que l’ACP est un outil de statistique exploratoire et ne permet pas généralement de tester des hypothèses. Un avantage de cet aspect exploratoire est que l’ACP peut être exécutée à différentes reprises, en éliminant / rajoutant des observations ou des variables, à condition que ces manipulations soient justifiées dans les interprétations.
Comment interpréter une matrice de corrélation ACP ?
Le premier résultat intéressant à analyser est la matrice des corrélations. On remarque le résultat évident que les taux de la proportion de gens étant agés de plus et moins de 65 ans sont parfaitement corrélés (r = -1). Les deux variables sont donc redondantes. On remarque l'immigration provenant d'autres états des USA est très peu corrélée avec les autres variables, y compris avec l’immigration provenant de pays étrangers. Cela indique que les raisons d'immigration sont sûrement différentes pour les deux populations concernées.

Comment interpréter les valeurs propres dans l'analyse en composantes principales ?
Le tableau suivant et le graphique associé sont liées à un objet mathématique, les valeurs propres, qui sont heureusement liées à un concept très simple : la qualité de la projection lorsque l'on passe de N dimensions (N étant le nombre de variables, ici 7) à un nombre plus faible de dimensions. Dans notre cas, on voit que la première valeur propre vaut 3.567 et représente 51% de la variabilité. Cela signifie que si l'on représente les données sur un seul axe, alors on aura toujours 51% de la variabilité totale qui sera préservée.
A chaque valeur propre correspond un facteur. Chaque facteur est en fait une combinaison linéaire des variables de départ. Les facteurs ont la particularité de ne pas être corrélés entre eux. Les valeurs propres et les facteurs sont triés par ordre décroissant de variabilité représentée.
De manière générale, facteur = dimension d’ACP = axe d’ACP.
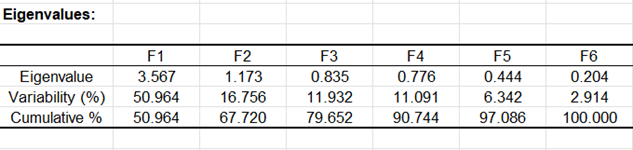
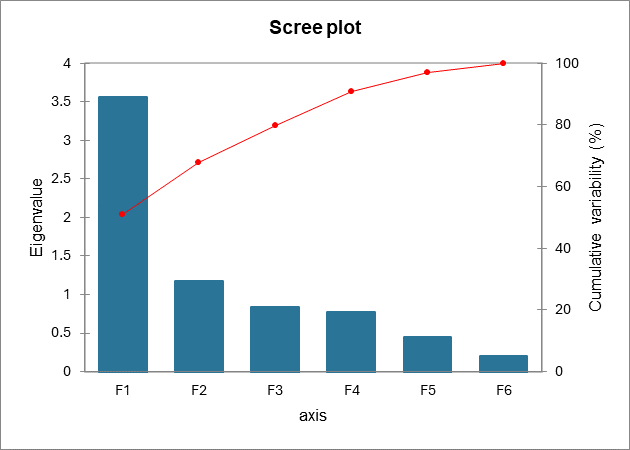
Idéalement, les deux premières valeurs propres correspondent à un % élevé de la variabilité, si bien que la représentation sur les deux premiers axes factoriels est de bonne qualité. Dans notre exemple, cela n'est pas tout à fait le cas, d'où la nécessité de valider les hypothèse formulées par l'utilisation des graphiques sur les facteurs F1 et F2 d'une part, et F1 et F3 d'autre part. Nous voyons ici que le nombre de facteurs est 6, alors que nous avions au départ 7 variables. Cela est dû aux deux variables redondantes. On comprend bien que l'information puisse être synthétisée sur 6 dimensions. Le nombre de dimensions "utiles" maximum est automatiquement détecter par la méthode utilisée.
Comment interpréter les résultats liés aux variables de l'ACP ?
Le premier graphique particulier à la méthode est le cercle des corrélations (voir ci-dessous le cercle sur les axes F1 et F2). Il correspond à une projection des variables initiales sur un plan à deux dimensions constitué par les deux premiers facteurs. Lorsque deux variables sont loin du centre du graphique, alors si elles sont : proches les unes par rapport aux autres, alors elles sont significativement positivement corrélées (r proche de 1), orthogonales les unes par rapport aux autres, alors elles sont significativement non-corrélées (r proche de 0), symétriquement opposées par rapport au centre, alors elles sont significativement négativement corrélées (r proche de -1).
Lorsque les variables sont relativement proches du centre du graphique, alors toute interprétation est hasardeuse, et il est nécessaire de se référer à la matrice de corrélations à d'autres plans factoriels pour interpréter les résultats. Dans notre exemple, nous pourrions déduire du graphique ci-dessous que les variables Immigration domestique, et Immigration Internationale sont corrélées, alors qu'elles ne le sont pas, ce que l'on peut voir sur la matrice des corrélations ou sur le cercle des corrélations sur les axes F1 et F3. En revanche, on voit bien la forte corrélation entre le taux de mortalité et le taux de personnes dont l'âge est supérieur à 65 ans.
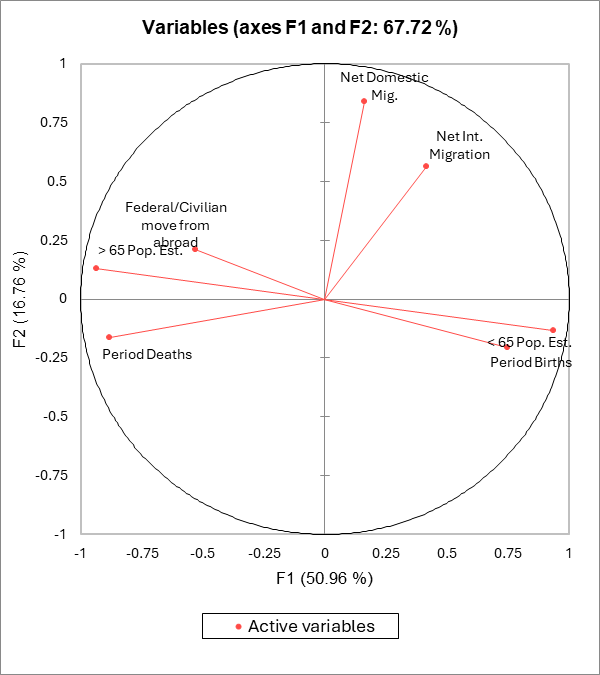
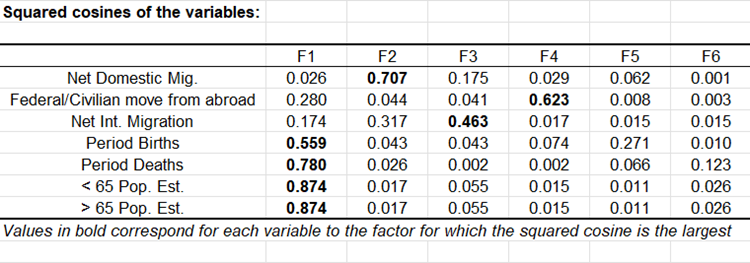
Le cercle des corrélations est aussi utile pour interpréter la signification des axes. Dans notre cas, l'axe F1 est clairement lié à l'âge de la population et à son renouvellement, alors que l'axe F2 est essentiellement lié à l'immigration domestique. Ces tendances sont particulièrement intéressantes à dégager pour l'interprétation du graphique des individus (voir ci-dessous). Pour confirmer le fait qu'une variable est fortement liée à un facteur, il suffit de consulter la table des cosinus : plus le cosinus est élevé (en valeur absolue), plus la variable est liée à l'axe. Plus le cosinus est proche de zéro, moins la variable est liée à l'axe. Dans notre cas, nous voyons que ce qui concerne l'immigration internationale sera mieux interprétée sur les F2/F3.
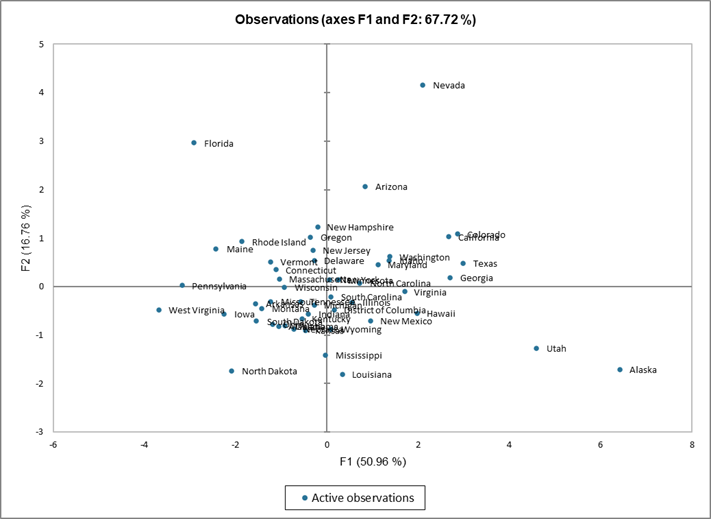
How to interpret results related to observations in PCA?
Le graphique ci-dessous correspond à l'un des objectifs de l'ACP. Il permet de représenter les individus sur une carte à deux dimensions, et ainsi d'identifier des tendances. On voit dans notre exemple que sur la base des variables démographiques dont on dispose, le Nevada et la Floride sont assez particuliers, de même que l'Utah et Alaska qui semblent partager des caractéristiques : en regardant les données, on s'aperçoit que ces deux états ont une population nettement plus jeune que la moyenne, et une natalité très élevée.
Cliquez pour voir le graphique en trois dimensions généré par XLSTAT-3DPlot sur les trois premiers axes factoriels.
Utiliser une ACP en amont d'une régression
L'Analyse en Composantes Principales est souvent utilisée avant une régression car elle permet d'éviter d'utiliser des variables redondantes, ou avant une classification car elle permet d'identifier la structure de la population et éventuellement de déterminer le nombre de groupes à construire. Les données utilisées dans ce tutoriel sont aussi utilisées dans le tutoriel sur la Classification Ascendante Hiérarchique. En tenant compte des remarques faites ci-dessus, la variable "pop >65" a été supprimée afin de ne pas rendre le poids des variables liées à l'âge trop important pour le regroupement des états.
Aller plus loin
Rajouter des variables supplémentaires sur l’ACP
Il est possible de rajouter des variables supplémentaires à l’ACP une fois qu’elle a été calculée. Ceci peut augmenter la qualité d’interprétation. Dans XLSTAT, ces variables peuvent être sélectionnées sous l’onglet données supplémentaires. de la boîte de dialogue de l’ACP. Les variables supplémentaires se divisent en deux types :
-
Variables supplémentaires qualitatives : elles permettent de colorer les observations sur le plan d’ACP en fonction de leur appartenance aux différentes catégories de la variable. Dans l’exemple de ce tutoriel, nous aurions pu rajouter une colonne mentionnant si l’état est plutôt républicain ou plutôt démocrate.
-
Variables supplémentaires quantitatives : ces variables peuvent être ajoutées pour voir la manière dont elles sont corrélées avec les différentes variables ayant servi pour construire l’ACP. Dans la situation où l’ACP est exécutée en amont d’une régression, les variables explicatives peuvent être utilisées pour construire l’ACP et la variable dépendante peut être introduite en tant que variable supplémentaire. Ceci peut aider à détecter grossièrement les variables explicatives ayant l’impact le plus important sur la variable dépendante.
Lancer une Classification Ascendante Hiérarchique (CAH) depuis une ACP
Vous pouvez également lancer une CAH en cliquant sur le bouton situé sous le tableau des coordonnées des observations. Une flèche orange vous permet d'accéder directement à la fin du tableau si celui-ci comporte de nombreuses variables.
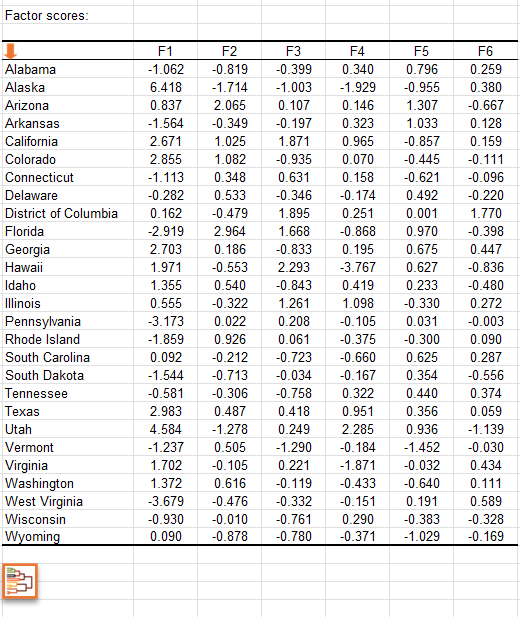
En cliquant sur ce bouton, la boite de dialogue de la CAH est alors automatiquement configurée et vous n'avez plus qu'à cliquer sur le bouton OK afin de lancer l'analyse.
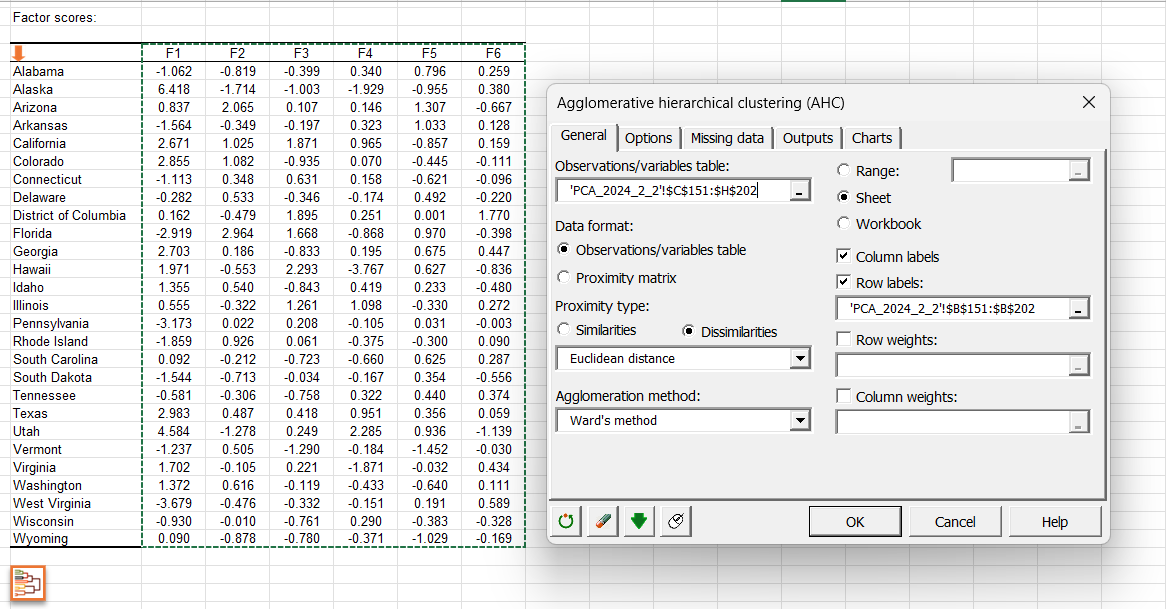
Cliquez ici pour voir comment interpréter les résultats de l'analyse CAH.
Visionner notre vidéo sur la ACP
La vidéo suivante aborde la théorie autour de l'ACP et son implémentation avec XLSTAT :
Cet article vous a t-il été utile ?
- Oui
- Non
