Création et analyse d'un Réseau Bayésien dans Excel

Ce tutoriel explique comment créer et analyser un réseau bayésien dans Excel avec XLSTAT.

Un réseau bayésien est un outil d’analyse statistique basé sur l’utilisation d’un graphe orienté acyclique accompagné d’une table de probabilités. Extrêmement populaire en intelligence artificielle, il sert principalement à représenter une connaissance et ses incertitudes. C’est un outil d’aide à la décision dont la fonction principale est de faire apparaître les relations de causalités entre des variables.

Jeu de données pour effectuer une analyse d’un réseau bayésien

Les données sont issues du livre « Réseaux bayésiens avec R » et sont utilisées pour déterminer les facteurs expliquant l’usage de certains transports par une population. Nous disposons de 6 variables : l’âge de la personne (Age), son sexe (S), son niveau d’études (E), son type de profession entre libéral et non libéral (Prof), la taille de la commune où se trouve son domicile (D) et le moyen de transport (T) le plus utilisé par la personne. La première variable est quantitative alors que toutes les autres sont qualitatives. Leurs modalités sont résumées dans le tableau ci-dessous :

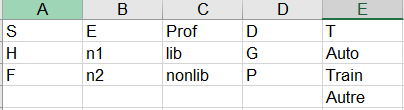
L'objectif de ce tutoriel est d’identifier les traits d’une population, parmi ceux évalués, sur l’usage de la voiture, du train et des autres moyens de transport.

Créer et analyser un réseau bayésien

Il faut tout d’abord construire le réseau bayésien modélisant notre problématique, c’est-à-dire dessiner le graphe et définir les tableaux de probabilités. Nous choisissons celui proposé dans le livre « Réseaux bayésiens avec R ».

Pour commencer, démarrez XLSTAT puis cliquez sur le menu XLSTAT / Fonctions avancées / Réseaux bayésiens / Nouveau projet comme ci-dessous pour ouvrir un nouveau projet.

La boîte de dialogue Options apparaît.

Vous avez le choix de construire un réseau bayésien selon le mode classique, qui nécessite l’utilisation d’un jeu de données, ou le mode expert, qui permet à l’utilisateur de définir lui-même étape par étape les données. Dans ce tutoriel, nous choisissons le mode classique.

Un classeur contenant deux feuilles s’ouvre. La première, nommée Data, est utilisée pour copier/coller les données et la deuxième, appelée BNGraph, est utilisée pour dessiner le graphique.

Sur la feuille de dessin est visible une barre d’outils composée de 8 boutons qui servent aux différentes étapes de construction et d’analyse du réseau bayésien.

NB pour les utilisateurs MAC : pour des raisons techniques, la fenêtre de nommage des nœuds s’ouvre uniquement avec le deuxième bouton de la barre d’outils. Pour l’utiliser vous devez sélectionner avant un nœud avec Ctrl + clic gauche.

A. Dessiner le graphe associé au réseau bayésien

Commencez par placer les 6 variables à l’aide du bouton Nœud, le premier dans la barre d’outils. Pour cela, cliquez sur le bouton Noeud, puis cliquez sur la feuille de dessin là où vous voulez positionner votre nœud. Au positionnement, une fenêtre s’ouvre pour nommer votre nœud. Répétez cette action pour chacun des nœuds jusqu’à obtenir la disposition suivante des variables :

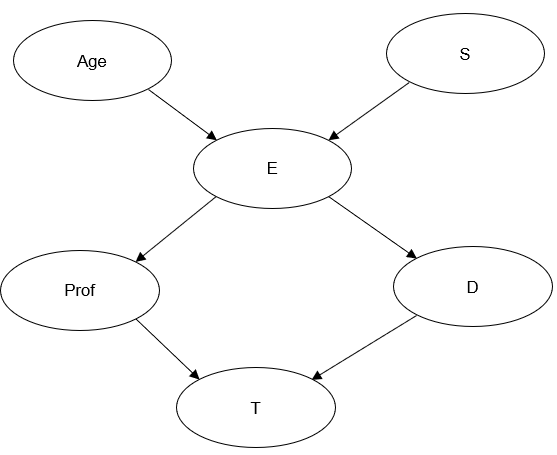
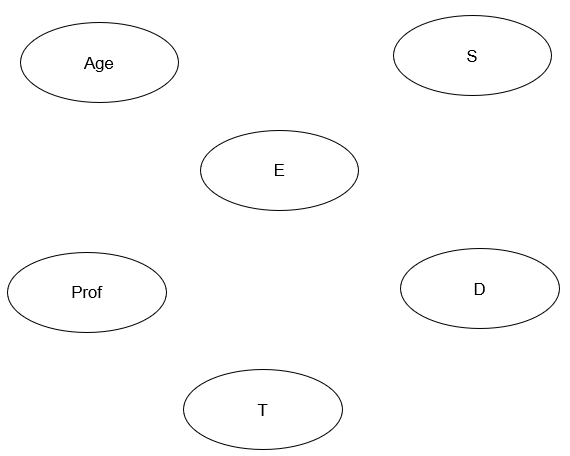Dessinez ensuite les relations entre les variables à l’aide du bouton Arc, le troisième dans la barre d’outils. Pour cela, sélectionnez un nœud causal (nœud parent), à l’origine de la flèche, avec la touche Ctrl et clic gauche, puis sélectionnez un nœud destinataire (nœud enfant) de la flèche, de la même manière. Dès que les deux nœuds sont présélectionnés dans le bon sens, cliquez sur le bouton arc. Une flèche apparaît alors entre les deux nœuds. Dans cet exemple, le niveau d’étude E dépend de l’âge de la personne. Cette dépendance se matérialise dans le graphe par une flèche partant du nœud Age et allant vers le nœud E. Créez l’ensemble des flèches jusqu’à obtenir le graphe suivant :

B. Définir les tableaux de probabilités

Pour tous les nœuds (variables) de votre graphe vous devez définir les valeurs prises pour chacune de leurs modalités en fonction de la structure de dépendance. Le nœud E a deux modalités dans ce réseau, n1 et n2, et dépend des nœuds Age et Sexe. Il faut donc définir les probabilités de la modalité n1, et aussi n2, sachant les modalités H et F du nœud sexe et les différentes classes d’âge de la population. Ces valeurs sont automatiquement générées à l’aide de l’outil disponible en cliquant sur le bouton Données, soit le cinquième bouton de la barre d’outils.

Une fois activé une boite de dialogue apparaît avec deux onglets.

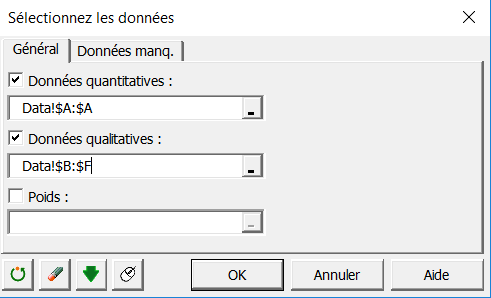Dans l'onglet Général, sélectionnez les données de la feuille Data. Dans notre exemple, on sélectionne les colonnes B à F en tant que données qualitatives et la colonne A en tant que données quantitatives.

Dans l’onglet Données manquantes, cochez la première option qui permet de stopper les calculs en présence de données manquantes.

Après avoir cliqué sur le bouton OK, une nouvelle feuille Excel apparaît dans le classeur avec le nom tableaux de probabilités dans laquelle sont affichées les probabilités de chaque nœud. Au début de la feuille se trouve les statistiques descriptives de vos données.

On voit par exemple que la variable Age a 3 modalités et que la dernière tranche d’âge est la plus fréquente dans ce jeu de données.

Une fois tous les tableaux remplis, le réseau bayésien est prêt à être analysé.

C. Lancer l’analyse du réseau bayésien

Vous pouvez cliquer sur le bouton Lancer l’analyse situé en dessous des tableaux de probabilités ou sur le septième bouton de la barre d’outils (bouton play).

Une boite de dialogue apparaît avec quatre onglets. Dans l'onglet Général, vérifiez le nom de la feuille présélectionnée contenant les tableaux de probabilités.

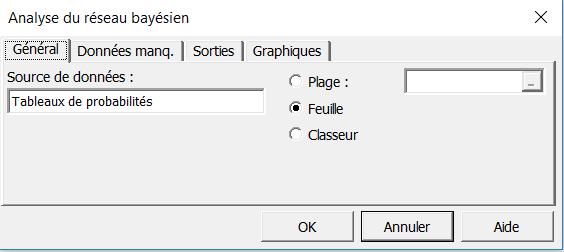Dans les onglets Données manquantes, sorties et graphiques gardez les options cochées par défaut.

Cliquez enfin sur le bouton OK pour démarrer les calculs. Les résultats sont affichés dans une nouvelle feuille nommée Analyse d’un réseau bayésien.

Interpréter les résultats de l’analyse d’un réseau bayésien

Les résultats sont des tableaux et des graphiques présentant les distributions de probabilités marginales de chaque nœud, les distributions de probabilités jointes de chaque clique et les distributions de probabilités conditionnelles.

Pour l’échantillon de la population donnée dans ce tutoriel, l’usage de la voiture est majoritaire par rapport aux autres moyens de transport étudié, presque près de la moitié des gens.

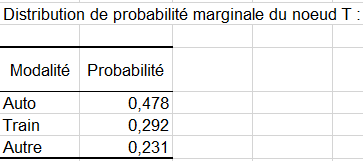
Les probabilités marginales nous apprennent également que cette population est constituée pour moitié d’hommes et de femmes, que les individus sont majoritairement plus diplômés n1 que n2 (69% contre 31% respectivement) avec quasiment la même proportion de profession libérale et non libérale (47,9% contre 52,1% respectivement) et habite plus souvent dans des grosses villes (61, 9% contre 38,1% respectivement).

Les probabilités conditionnelles nous donnent de l’information plus précise. Par exemple, on sait qu’une personne de profession libérale utilise d’avantage la voiture comparé à une personne de profession non libérale quand on compare la première et la quatrième ligne de ce tableau,

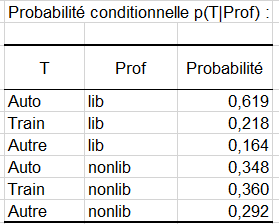
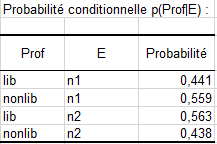
On apprend également lorsqu’on regarde la première et la quatrième ligne du tableau suivant, que la proportion de personnes en profession libérale diplômées n2 est légèrement au-dessus de la moyenne comparé aux personnes diplômées n1.

Aller plus loin avec les réseaux bayésiens

Il est possible de modifier une ou plusieurs valeurs dans les tableaux de probabilités à l’aide du bouton Editeur, sixième bouton de la barre d’outils.

Pour cela sélectionnez un nœud de la feuille BNGraph avec Ctrl + clic gauche puis cliquez sur le bouton. Une fenêtre s’ouvre alors, comme celle-ci pour le nœud Prof :

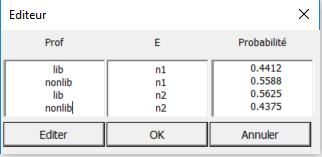
Nous modifions la valeur de ces probabilités en respectivement 0 et 1, pour les deux modalités du nœud E, de façon à conserver la somme égale à 1 pour chacune. Pour ce faire, sélectionnez la première valeur et cliquez sur Edit. Saisissez la nouvelle valeur et cliquez sur OK. De la même façon, modifiez les trois autres valeurs de façon à obtenir ce nouveau tableau de probabilités :

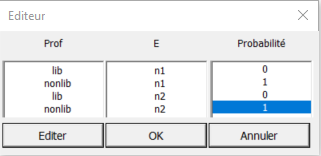Pour que ces nouvelles valeurs soient prises en compte dans le tableau des probabilités de la feuille Excel, cliquez à nouveau sur OK. Vous pouvez alors lancer une nouvelle analyse sur ce réseau bayésien connaissant les nouvelles valeurs des probabilités conditionnelles du nœud Prof.

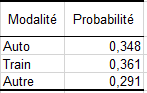Pour ce réseau bayésien et cet échantillon de valeurs données, l’usage du train est privilégié dans une proportion légèrement supérieure à celle dédiée à l’usage de la voiture.