Modes de calcul et chemin optimal d'un arbre de décision dans Excel

Ce tutoriel explique les différentes méthodes de calcul et la notion de chemin optimal pour un arbre de décision sous Excel en utilisant XLSTAT.

Jeu de données pour travailler sur les calculs d’un arbre de décision

But de ce tutoriel

L’objectif est de partir d’un arbre de décision existant, basé sur un exemple concret, et de découvrir les différentes méthodes de calcul. Une entreprise prête à lancer un nouveau produit sur le marché, se demande quel canal publicitaire privilégier. Nous allons l’aider à faire un choix en fonction de l’objectif visé : maximiser son gain ou bien le minimiser, en considérant son degré d’aversion au risque. La notion de chemin optimal est aussi présentée. Si vous souhaitez en apprendre plus sur la construction de l’arbre alors aller sur ce tutoriel .

Modes de calcul d’un arbre de décision et chemin optimal avec XLSTAT

Dans XLSTAT, il existe deux modes de calcul pour vous aider dans la prise de décision. Le gain, somme des coûts et profits, peut être maximisé si vous souhaitez optimiser votre profit ou minimisé si vous souhaitez optimiser votre coût. Ces deux modes de calcul sont agrémentés de la possibilité d'avoir un gain calculé à partir d'une fonction d'utilité exponentielle où l’utilité R est paramétrable. Une utilité positive traduit une aversion au risque plus ou moins prononcée tandis qu’une utilité négative traduit une recherche de risque. Une utilité nulle revient à considérer le gain comme la somme des coûts et profits.

Nous partons d’un arbre existant, fourni dans le jeu de données. Commençons par afficher l’arbre avec pour objectif de maximiser le gain. Pour ouvrir la boîte de dialogue de paramétrage de l’arbre, faites un clic droit sur le bloc de l’arbre (premier bloc en haut) et sélectionnez XLDTREE/Ouvrir la boîte de dialogue de paramétrage de l’arbre sélectionné.

Dans l’onglet Général, sélectionnez les options Maximiser le gain et chemin optimal pour : Valeur attendue.

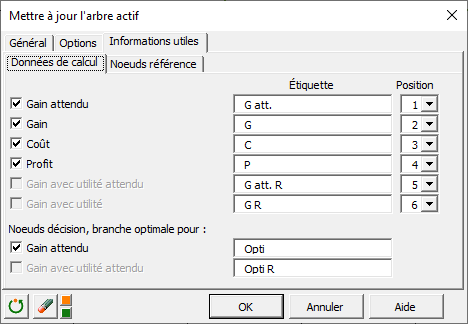
Dans l’onglet Informations utiles/Données de calcul, sélectionnez les informations à afficher avec l’étiquette voulue et la position. Puis cliquez sur le bouton OK.

Pour mettre le chemin optimal en évidence (en vert), faites un clic droit sur le bloc de l’arbre (premier bloc en haut) et sélectionnez XLDTREE/Mettre en surbrillance le chemin optimal pour l’arbre sélectionné. Le chemin optimal est recalculé à chaque modification de valeur (les cellules sur fond coloré).

Voici l’arbre obtenu :

Le chemin optimal nous dirige vers les extrémités de l’arbre répondant le mieux à l’objectif de départ : maximiser le gain. Il dépend du gain attendu de chaque nœud et son comportement est différent selon le type de nœud. Pour un nœud décision, il passe par la branche dont le gain répond le mieux au mode de calcul choisi. Pour un nœud chance, il passe par toutes les branches du nœud. En effet, il n'est pas possible de savoir à l'avance quelle branche sera réalisée, peu importe sa probabilité de réalisation. Le gain attendu tient compte de ce comportement puisqu'il est la somme pondérée (par la probabilité de réalisation) du gain attendu du nœud enfant de chaque branche.

Prenons le cas d’un investissement dans la publicité internet. Nous pouvons observer les chiffres suivants :

• Dans le cas de ressources internes :

Hypothèse CA attendu	Probabilité	Profit attendu par hypothèse	Profit attendu pondéré par hypothèse	Profit attendu de l'option	Coût de l'option	Gain attendu
Haute	60%	30 000	18 000 (60% x 30 000)	26 000 (18 000 + 8 000)	-8 000	18 000 (26 000 - 8 000)
Basse	40%	20 000	8 000 (40% x 20 000)

• Dans le cas de ressources externes :

Hypothèse CA attendu	Probabilité	Profit attendu par hypothèse	Profit attendu pondéré par hypothèse	Profit attendu de l'option	Coût de l'option	Gain attendu
Haute	70%	40 000	28 000 (70% x 40 000)	35 500 (28 000 + 7 500)	-15 000	20 500 (35 500 - 15 000)
Basse	30%	25 000	7 500 (30% x 25 000)

Il semble donc plus intéressant, si nous souhaitons maximiser le gain, d’opter pour une entreprise externe afin de développer la publicité internet. Si nous comparons le gain attendu de chaque canal publicitaire alors cette option reste encore le meilleur choix. Une telle décision doit prendre en compte d’autres facteurs mais ceux-ci peuvent facilement être ajoutés à l’arbre afin d’affiner son analyse.

Nous partons toujours du même arbre. Nous allons maintenant afficher l’arbre avec pour objectif de minimiser le gain. Dans l’onglet Général de la boîte de dialogue de paramétrage de l’arbre, sélectionnez l’option Minimiser le gain, puis cliquez sur le bouton OK.

Voici l’arbre obtenu :

Le chemin optimal nous dirige vers les extrémités de l’arbre répondant le mieux à l’objectif de départ : minimiser le gain. Prenons le cas d’un investissement dans les réseaux sociaux. Nous pouvons observer les chiffres suivants :

• Dans le cas de ressources internes :

Hypothèse CA attendu	Probabilité	Profit attendu par hypothèse	Profit attendu pondéré par hypothèse	Profit attendu de l'option	Coût de l'option	Gain attendu
Haute	50%	20 000	10 000 (50% x 20 000)	17 500 (10 000 + 7 500)	-5 000	12 500 (17 500 - 15 000)
Basse	50%	15 000	7 500 (50% x 15 000)

• Dans le cas de ressources externes :

Hypothèse CA attendu	Probabilité	Profit attendu par hypothèse	Profit attendu pondéré par hypothèse	Profit attendu de l'option	Coût de l'option	Gain attendu
Haute	60%	25 000	15 000 (60% x 25 000)	22 200 (15 000 + 7 200)	-10 000	12 200 (22 200 - 10 000)
Basse	40%	18 000	7 200 (40% x 18 000)

Il semble donc plus intéressant, si nous souhaitons minimiser le gain, d’opter pour une entreprise externe afin de développer la publicité sur les réseaux sociaux. Si nous comparons le gain attendu de chaque canal publicitaire alors cette option reste encore le meilleur choix.

Nous partons toujours du même arbre. Nous allons maintenant afficher l’arbre avec pour objectif de maximiser le gain mais en utilisant la fonction d’utilité. Ouvrez la boîte de dialogue de paramétrage de l’arbre.

Dans l’onglet Général, sélectionnez les options Maximiser le gain et chemin optimal pour : Utilité attendue, cochez la case R si fonction d’utilité et renseignez votre utilité. Il est possible de renseigner l’utilité directement mais il peut être intéressant de lire l’utilité dans une cellule de la feuille (comme dans notre cas) afin de faire varier ce paramètre sans avoir à repasser par la boîte de dialogue.

Dans l’onglet Informations utiles/Données de calcul, sélectionnez les informations à afficher avec l’étiquette voulue et la position. Puis cliquez sur le bouton OK.

Voici l’arbre obtenu :

Le chemin optimal nous dirige vers les extrémités de l’arbre répondant le mieux à l’objectif de départ : maximiser le gain avec utilité. Comme pour le cas du gain sans utilité, opter pour une entreprise externe afin de développer la publicité internet semble être le choix répondant le mieux à notre besoin.

Aller plus loin

Il est possible de mettre en évidence le chemin optimal pour un nœud en particulier. Pour cela il suffit de faire un clic droit sur le bloc du nœud de départ et de sélectionner XLDTREE/Mettre en surbrillance le chemin optimal à partir du nœud sélectionné. La même opération permet d’enlever le chemin optimal. Tant que l'option chemin optimal est activée, celui-ci est automatiquement recalculé et son affichage mis à jour, à chaque modification de l'arbre.

Il est également possible de forcer une branche à faire partie du chemin optimal. Cela peut être utile lorsque vous revenez plus tard sur un arbre existant, à un moment où certains choix ont déjà été faits ou réalisés. Une seule branche, parmi toutes celles de l'arbre, peut-être forcée. Si une autre branche était déjà forcée alors elle ne le serait plus. La branche forcée à son nom affiché dans une couleur différente de celle des autres noms de branches.