Analyse Procustéenne Généralisée dans Excel
Ce tutoriel explique comment calculer et interpréter une Analyse procustéenne généralisée (GPA) avec Excel en utilisant XLSTAT.
Analyse Procustéenne Généralisée
L'Analyse Procustéenne Généralisée (AGP, ou Generalized Procrustes Analysis ou GPA en anglais) est souvent utilisée en analyse sensorielle avant une cartographie des préférences pour réduire les effets d'échelle et obtenir une configuration bi ou tri-dimensionnelle consensuelle (ou configuration moyenne).
Cette méthode est aussi utilisée en marketing pour comparer les proximités entre les termes utilisés par différents experts pour décrire des produits.
Jeu de données pour réaliser une Analyse Procustéenne Généralisée
Les données correspondent à une étude au cours de laquelle une équipe marketing souhaite comparer comment quatre fromages légèrement différents proposés par la R&D sont perçus.
Pour cela, on a demandé à 10 experts d'évaluer plusieurs choix chacun des fromages sans qu'ils puissent visuellement différencier les fromages. Les notes utilisées ici sont les moyennes obtenus par chaque fromage, pour chaque expert, suivant trois critères : l'acidité, l'étrangeté, la fermeté.
Notre but est de transformer les données de manière à éliminer les effets d'échelle (certains experts vont avoir tendance à noter sur une gamme de notes plus large que d'autres), de position (certains experts vont avoir tendance à utiliser des notes plus basses que d'autres, et inversement), pour obtenir une configuration consensuelle qui pourra ensuite être utilisée pour une analyse de type PREFMAP .
Paramétrer une Analyse Procustéenne Généralisée
Pour activer la boîte de dialogue de l'Analyse Procustéenne Généralisée, choisissez la commande Analyse de données sensorielles /Analyse Procustéenne Généralisée ou Analyse de données multitableaux / Analyse Procustéenne Généralisée.
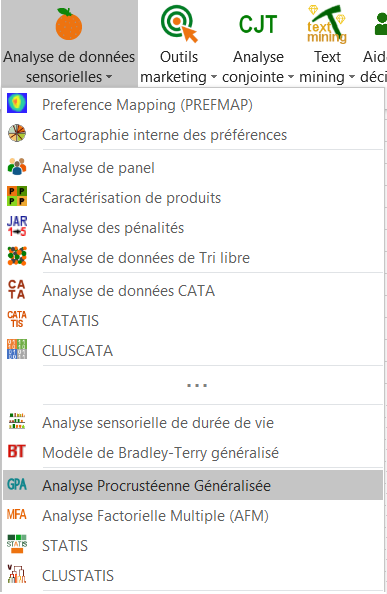
Une fois le bouton cliqué, la boîte de dialogue apparaît.
Vous pouvez alors sélectionner les configurations (une configuration correspond ici à l'ensemble des notes données par un expert).
Le nombre de configurations doit ensuite être saisi. Il y a ici 10 tableaux contigus correspondant aux dix experts.
Comme les 10 configurations ont chacun trois dimensions, l'option Egal est choisie pour le nombre de dimensions. Lorsque le nombre de dimensions varient pour les différentes configurations, il faut sélectionner une colonne contenant le nombre de dimensions des différentes configurations.
Les étiquettes des configurations et des produits sont aussi sélectionnées donc il faut sélectionnées les options Libellés des variables et Libellés des observations.
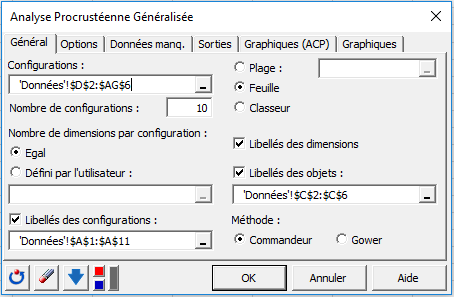
Les options suivantes ont été choisies dans les différents onglets.
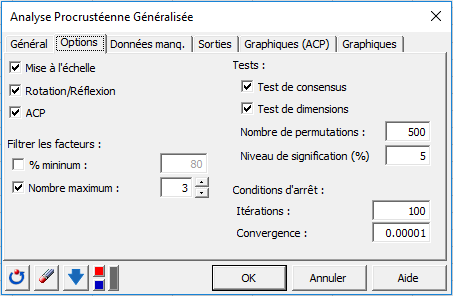
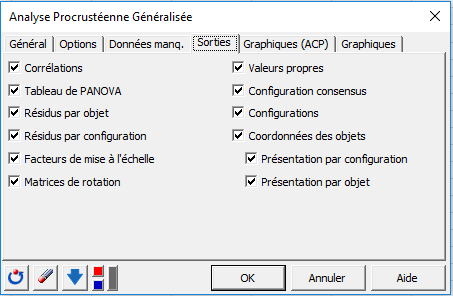
Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.
Interpréter les résultats d'une Analyse Procustéenne Généralisée
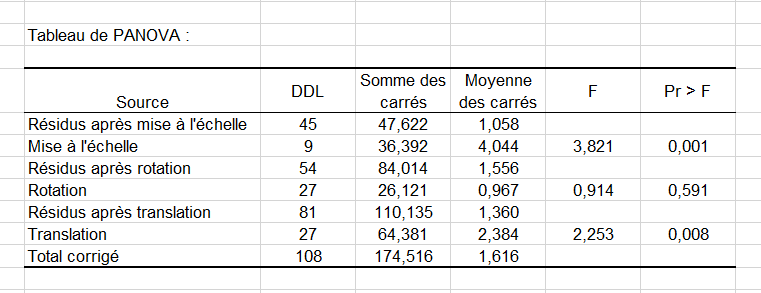
Le premier tableau correspond au tableau de PANOVA donnant l'efficacité relative des différentes transformations. On voit ici la mise à l'échelle a eu un impact prépondérant sur la réduction de la variabilité des configurations.
Le second tableau et le graphique correspondant donnent les résidus par objet après les transformations de l'Analyse Procustéenne Généralisée. On peut voir que le résidu le plus faible obtenu pour le fromage F3. Cela indique que ce produit fait l'objet d'un consensus.

Le troisième tableau et le graphique correspondant donnent les résidus par configuration après les transformations de l'Analyse Procustéenne Généralisée. On peut voir que le résidu le plus important correspond à l'expert n°2, ce qui indique que l'expert n°2 est le plus éloigné du consensus, autrement dit que les notes qu'il a données sont sensiblement différentes de celles des autres experts.

Le graphique suivant permet de visualiser les facteurs de mise à l'échelle de l'Analyse Procustéenne Généralisée. Un facteur plus petit que 1 indique que l'expert en question a eu tendance à utiliser une gamme de notes plus importante que les autres experts. Un facteur plus grand que 1 indique que l'expert en question a eu tendance à utiliser une gamme de notes moins importante que les autres experts. On peut voir ici que les experts 1 et 3 ont eu tendance à utiliser un intervalle de notation plus petit que les autres experts.

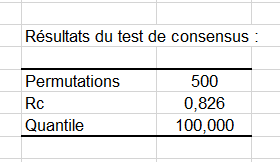
Un test de consensus est alors réalisé pour vérifier si la configuration consensus (calculée comme la configuration moyenne après les différentes transformations) correspond à un véritable consensus. Ce test de permutation permet de déterminer si la valeur observée de Rc (Rc correspond à la proportion de la variance totale expliquée par la configuration consensus) est sensiblement plus élevée que 95% des résultats obtenus après permutation.

Un autre test de permutation est utilisé pour vérifier combien de dimensions doivent être retenues pour l'affichage les résultats. Nous voyons ici que pour la troisième dimension, la valeur du F est inférieure au 95ième percentile de la distribution empirique. Ainsi nous pouvons conclure que deux dimensions sont suffisantes.

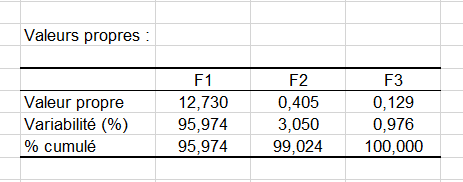
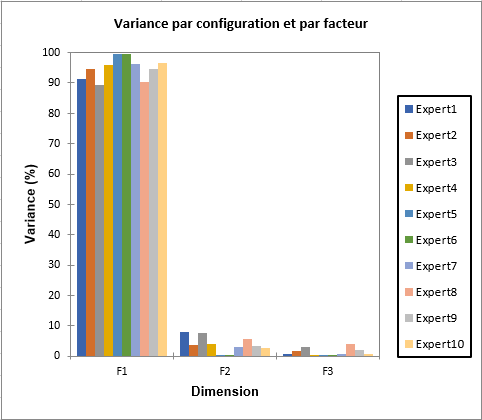
Les résultats qui suivent concernent l'ACP qui est réalisée après l'Analyse Procustéenne Généralisée. Il s'agit ici d'une ACP non normée. Alors que l'Analyse Procustéenne Généralisée inclut déjà des rotations optimales appliquées à chacune des configurations pour obtenir un consensus, l'ACP permet d'appliquer une transformation à la configuration consensuelle de manière à obtenir une représentation optimale sur les premiers axes. La transformation de l'APC est ensuite appliquée à chacune des configurations correspondant à chaque expert. Les valeurs propres indiquent la proportion de la variabilité totale représentée sur chacun des axes factoriels. On peut voir que 99% de la variabilité est représentée sur les deux premiers axes. Lorsque la variabilité est analysée au niveau de chaque expert, on peut voir que la situation est analogue pour l'ensemble des experts.
Les résultats sont ensuite divisés en deux parties: ceux qui concernent la configuration consensuelle, et ceux qui concernent chaque configuration individuelle. Les coordonnées des objets pour la configuration consensuelle peuvent ensuite être utilisées dans une analyse de type PREFMAP comme les coordonnées des produits sur la carte de préférence. Sur le cercle des corrélations on observe que l'Etrangeté est la plupart du temps situé sur la partie négative du premier axe, et que l'acidité et la fermeté sont souvent sur la partie positive, avec parfois une corrélation entre les deux. L'Etrangeté qui se trouve à l'origine du graphique correspond à l'expert 6 qui n'a pas fourni de note pour ce critère pour les 4 fromages.

Les deux graphiques suivants sont les cartes factorielles, colorées respectivement selon les configurations ou selon les objets (ici les fromages). Les points sont tous proches du premier axe parce que 95% de la variabilité est concentrée sur le premier axe, et parce que XLSTAT affiche les résultats sur des graphiques orthonormés.


Afin de rendre le graphique plus lisible, nous avons changé les options d'échelle (comme on peut le faire avec tout graphique Excel, éventuellement en utilisant l'outil AxesZoomer de XLSTAT). On obtient alors le graphique suivant :

On peut voir que les fromages F1 et F3 sont nettement séparés sur le graphique, alors que la distinction entre F2 et F4 est moins évidente. Cela signifie que les experts parviennent à un consensus pour F1 et F3, alors que pour F2 et F4 la proximité des produits semblent rendre le consensus moins évident.
Cet article vous a t-il été utile ?
- Oui
- Non