Apprentissage d'une régression par machines à vecteurs de support dans Excel
Ce tutoriel explique comment mettre en place, entraîner et interpréter une régression par Machines à Vecteurs de Support (SVM) dans Excel en utilisant le logiciel de statistiques XLSTAT.
Jeu de données pour entraîner un modèle de régression par SVM
Le jeu de données représente les caractéristiques des abalones, qui sont de gros mollusques gastropodes. Pour connaître l’âge d’un abalone il faut colorier les anneaux (RINGS) et les compter au microscope, ce qui reste un travail fastidieux. On cherchera donc à prédire l’âge des abalones avec des mesures autres que le nombre d’anneaux, qui sont plus simples à récupérer.
But de ce tutoriel
Le but de ce tutoriel est d’apprendre à mettre en place et entraîner une régression par SVM, sur le jeu de données Abalone, pour voir les performances que nous obtenons sur un jeu de données de validation.
Mettre en place une régression par SVM dans Excel avec XLSTAT
Pour mettre en place une régression par SVM, cliquez sur Machine Learning / Machines à vecteurs de support comme indiqué ci-dessous :
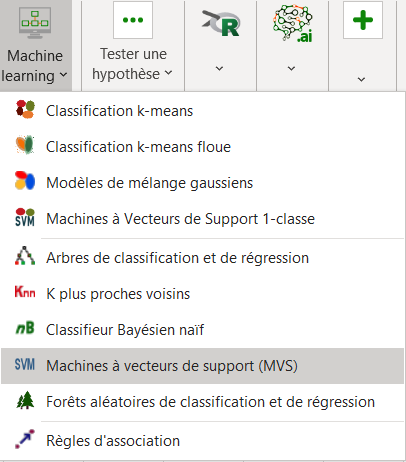 Après avoir cliqué sur le bouton, la boîte de dialogue SVM apparaît. Sélectionnez les données dans la feuille Excel.
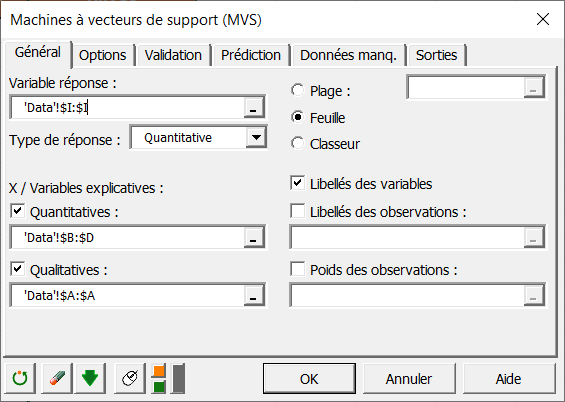
Après avoir cliqué sur le bouton, la boîte de dialogue SVM apparaît. Sélectionnez les données dans la feuille Excel.
Dans le champ intitulé variable réponse, sélectionnez la variable quantitative que vous souhaitez prédire. Dans notre cas, il s'agit de la colonne donnant le nombre d’anneaux.
Afin de faire une régression, sélectionnez Quantitative comme type de réponse.
Il faut également sélectionner des variables quantitatives et qualitatives en activant les deux options comme indiqué ci-dessous.
Dans le champ Quantitatives, sélectionnez les colonnes suivantes : - Length,
- Diameter,
- Height.
Dans le champ Qualitatives, sélectionnez la colonne avec les informations qualitatives : Sex.
Comme le nom de chaque variable est présent au début du fichier, assurez-vous que la case Libellés des variables soit bien cochée.
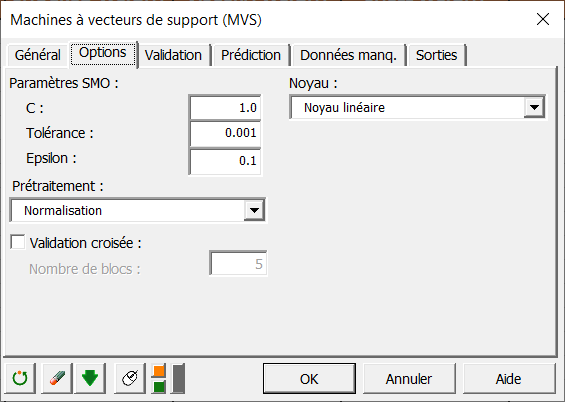
 Dans l'onglet Options, vous pouvez régler les paramètres pour la régression :
Dans l'onglet Options, vous pouvez régler les paramètres pour la régression :
Pour les paramètres SMO, le champ C correspond à la variable de régularisation. Elle traduit le montant autorisé d’erreurs plus grandes que ε. Dans notre cas, nous réglons ce paramètre à 1 mais il devra être positif.
Le paramètre de tolérance est un critère d'arrêt. Pour accélérer les calculs, vous pouvez augmenter la valeur de ce paramètre. Nous le laissons à sa valeur par défaut.
Le champ Epsilon est le paramètre qui crée le tube d’insensibilité de rayon ε et influe sur le nombre de vecteurs de support. Il sera de même laissé à sa valeur par défaut de 0.1 et devra être positif.
Pour le prétraitement, nous choisissons la normalisation et nous utiliserons des noyaux linéaires comme indiqué ci-dessous.
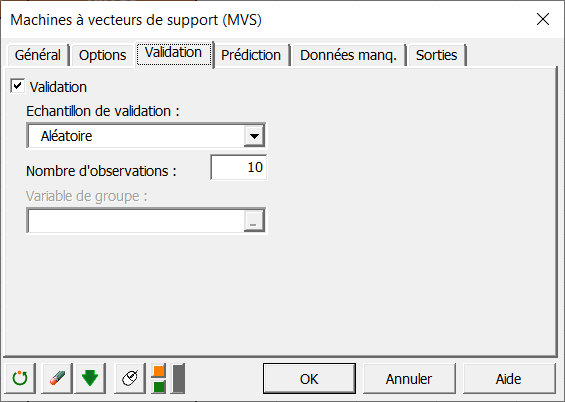
 Comme nous voulons voir les performances de notre régression, nous allons créer un échantillon de validation à partir du jeu d’apprentissage. Pour cela, dans l’onglet validation, nous cochons la case validation et sélectionnons 10 observations prises aléatoirement dans l’échantillon d’apprentissage :
Comme nous voulons voir les performances de notre régression, nous allons créer un échantillon de validation à partir du jeu d’apprentissage. Pour cela, dans l’onglet validation, nous cochons la case validation et sélectionnons 10 observations prises aléatoirement dans l’échantillon d’apprentissage :
 Finalement dans l’onglet sorties, sélectionnez les sorties comme indiqué ci-dessous :
Finalement dans l’onglet sorties, sélectionnez les sorties comme indiqué ci-dessous :
 Les calculs démarrent lorsque vous cliquez sur OK. Les résultats sont ensuite affichés.
Les calculs démarrent lorsque vous cliquez sur OK. Les résultats sont ensuite affichés.
Interpréter les résultats d’une régression par SVM
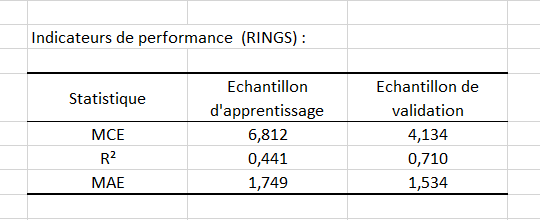
Le premier tableau donne des mesures de performance, qui nous permettent de juger la régression obtenue. Ici nous utilisons le carré moyen des erreurs, l'erreur absolue moyenne et le coefficient de détermination. Nous voulons un carré moyen des erreurs et une erreur absolue moyenne relativement petits tandis que nous espérons un coefficient de détermination le plus proche possible de 1. Ici, le coefficient de détermination pour l’échantillon de validation possède un score correct de 71%.
 Un résumé des caractéristiques de la régression optimisée obtenue est affiché par la suite. Vous pouvez voir sur la figure ci-dessous, que 70 observations ont été utilisées pour entraîner la méthode et 59 observations ont été identifiées comme vecteurs de support. Enfin, le biais, qui est l’origine de l’hyperplan, nous servira lors des calculs de régression pour notre échantillon de validation.
Un résumé des caractéristiques de la régression optimisée obtenue est affiché par la suite. Vous pouvez voir sur la figure ci-dessous, que 70 observations ont été utilisées pour entraîner la méthode et 59 observations ont été identifiées comme vecteurs de support. Enfin, le biais, qui est l’origine de l’hyperplan, nous servira lors des calculs de régression pour notre échantillon de validation.
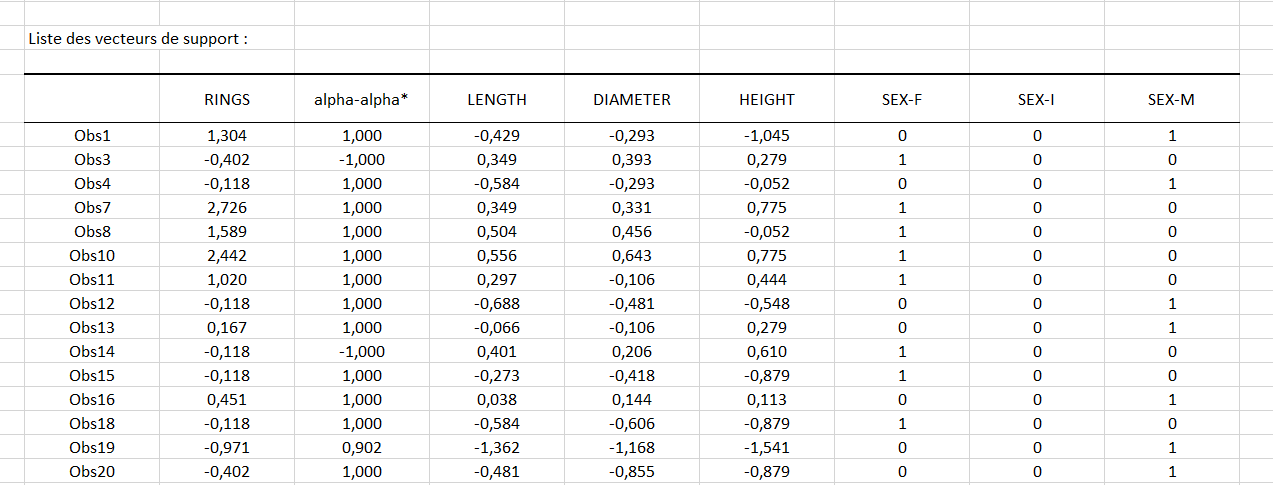
 Le second tableau, montré ci-dessous, donne la liste complète des 59 vecteurs de support avec leur coefficient alpha-alpha* associé, les valeurs de la variable réponse, les prédicteurs ayant subi un prétraitement ainsi que le tableau disjonctif des variables qualitatives.
Le second tableau, montré ci-dessous, donne la liste complète des 59 vecteurs de support avec leur coefficient alpha-alpha* associé, les valeurs de la variable réponse, les prédicteurs ayant subi un prétraitement ainsi que le tableau disjonctif des variables qualitatives.
 Enfin, vous pouvez voir les prédictions obtenues, grâce à la régression, pour chaque observation dans le tableau suivant :
Enfin, vous pouvez voir les prédictions obtenues, grâce à la régression, pour chaque observation dans le tableau suivant : 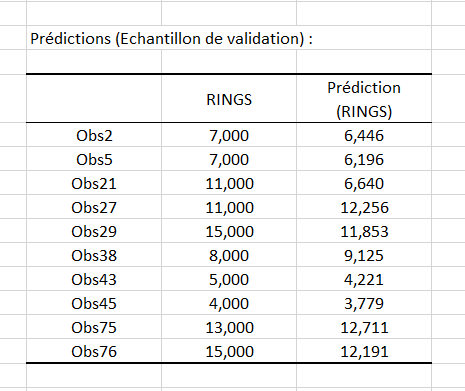
Cet article vous a t-il été utile ?
- Oui
- Non