Régression par les doubles moindres carrés dans Excel
Jeu de données utilisé pour la régression par les doubles moindres carrés
Les données correspondent à l’exemple de Kmenta sur l’offre et la demande alimentaire [Kmenta, J. (1971). Elements of Econometrics, 565- 582]. Les données sont composées de 5 variables : la consommation alimentaire par personne (FCH), le ratio entre le prix des denrées alimentaires et le prix général (RFP), le revenu disponible (DI), le ratio des années précédentes (RPP) et l’année de 1922-1941 (Year). Les variables FCH et RFP sont endogènes et les variables DI, RPP et Year sont exogènes.
But de ce tutoriel
On souhaite expliquer la consommation alimentaire par personne en fonction du ratio entre le prix des denrées alimentaires et le prix général et du revenu disponible.
Etant donné que l’une des variables explicatives est exogène, on utilise les variables DI, RPP et Year comme variables instrumentales et on estime les paramètres par la méthode des doubles moindres carrés.
Paramétrer une régression par la méthode des doubles moindres carrés
Une fois XLSTAT ouvert, sélectionnez la commande XLSTAT / Modéliser des données / Doubles moindres carrés, ou cliquez sur le bouton correspondant dans la barre de menu.

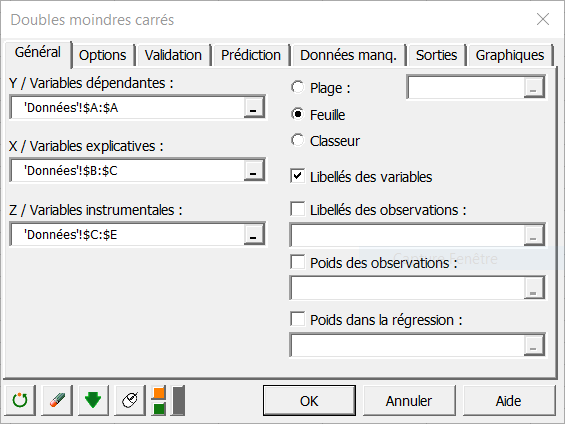
La boîte de dialogue Doubles moindres carrés apparaît.
Les données sont présentées sous forme d’un tableau constitué de 20 observations et de 5 variables. La variable FCH est la variable dépendante, les variables RFP et DI sont les variables explicatives et on utilise les variables DI, RPP et Year comme variables instrumentales. L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.
Dans l’onglet Options, on trouve la possibilité de régler le seuil de tolérance, le niveau des intervalles de confiance ainsi que la possibilité d’inclure ou non la constante dans le modèle. Nous choisissons ici de laisser les valeurs par défaut.

Lancez les calculs en cliquant sur OK. Les résultats sont affichés dans une nouvelle feuille Excel.
Interpréter les résultats
Les premiers résultats affichés sont les statistiques descriptives pour chaque variable. Ensuite vient le tableau des coefficients d'ajustement du modèle. Le R² (coefficient de détermination) donne une idée du % de variabilité de la variable à modéliser, expliqué par les variables explicatives. Plus ce coefficient est proche de 1, meilleur est le modèle.

On trouve ensuite le tableau d'analyse de la variance (voir ci-dessous). C'est à ce niveau que l'on teste si l'on peut considérer que les variables explicatives sélectionnées (RFP et DI) apportent une quantité d'information significative au modèle (hypothèse nulle H0) ou non. En d'autres termes, c'est un moyen de tester si la moyenne de la variable à modéliser suffirait à décrire les résultats obtenus ou non.

Le test du F de Fisher est utilisé. Etant donné que la probabilité associée au F est dans ce cas inférieure à 0.0001, cela signifie que l'on prend un risque de se tromper de moins de 0.01% en concluant que les variables explicatives apportent une quantité d'information significative au modèle.
Le tableau suivant fournit les détails sur le modèle (paramètres, écart-type, …) et est essentiel dès lors que le modèle doit être utilisé pour faire des prévisions, des simulations ou s'il doit être comparé à d'autres résultats.

On dispose ensuite d’outils permettant d’analyser les résidus du modèle tels que le graphique des résidus centrés réduits. Ce graphique permet de repérer rapidement et visuellement la présence de valeurs hors de l'intervalle [-2, 2].

Ici, aucune des valeurs ne sort de l’intervalle.
Cet article vous a t-il été utile ?
- Oui
- Non