Gage R&R pour données quantitatives dans Excel

Ce tutoriel explique comment calculer et interpréter l'analyse Gage R&R pour des données quantitatives avec Excel en utilisant XLSTAT.

Jeu de données pour contrôler et valider une méthode de mesure avec plusieurs mesures quantitatives obtenues par plusieurs opérateurs sur plusieurs pièces

Les données sont extraites d'une publication [Montgomery, D.C. (2001), Introduction to Statistical Quality Control, 4th edition, John Wiley & Sons].

Les données correspondent aux mesures sur un système avec 10 pièces et 3 opérateurs répétant chaque mesure 3 fois.

But de ce tutoriel

Le système d’analyse des mesures (MSA) ou le Gage R&R (Répétabilité et Reproductibilité) est une méthode pour contrôler et évaluer les processus de mesure. C’est utile pour déterminer à quoi est due la variation des mesures. Cette variabilité peut être causée par le système de mesure, par les opérateurs ou encore par les pièces. Le Gage R&R appliqué à des mesures quantitatives est basé sur deux méthodes communes : l’ANOVA et les tables de contrôle R.

Le mot “gage” réfère au fait que la méthodologie a pour but de valider des instruments ou des méthodes de mesure.

Lorsque les mesures sont des données quantitatives, deux méthodes sont disponibles pour l'analyse Gage R&R. La première est basée sur l'analyse de variance (ANOVA) et la seconde sur les cartes de contrôle R (Amplitude et moyenne).

La “répétabilité” désigne des mesures cohérentes (ne variant pas au-delà d’un certain seuil) pour une même pièce et un même opérateur. Si la répétabilité n’est pas satisfaisante, il faut s’interroger sur la qualité du système de mesure, ou entraîner les opérateurs qui n’ont pas une bonne répétabilité si jamais le système n’est pas responsable de la variabilité.

La “reproductibilité” désigne des mesures cohérentes (ne variant pas au-delà d’un certain seuil) pour une même pièce par des opérateurs différents. Si la reproductibilité n’est pas satisfaisante, il faut entraîner les opérateurs afin qu’ils obtiennent des résultats plus homogènes.

Le but d’une analyse R&R est ainsi d’identifier les causes de la variabilité et de prendre les mesures nécessaires pour la réduire.

Paramétrer un contrôle d'une méthode de mesure avec plusieurs mesures quantitatives obtenues par plusieurs opérateurs sur plusieurs pièces

Une fois XLSTAT lancé, sélectionnez le menu XLSTAT / SPC / Analyse du système de mesures (Gage R&R) / Quantitatives.

La boîte de dialogue Analyse du système de mesures (Gage R&R) / Quantitatives apparaît. Vous pouvez maintenant sélectionner les données sur la feuille Excel.

Activez l’option “Noms des variables” vu que la première ligne contient les noms des variables.

Sélectionnez les données dans l'onglet Général.

• Y / Mesures : colonne D,
• X / Opérateur : colonne A,
• Pièces : colonne B.

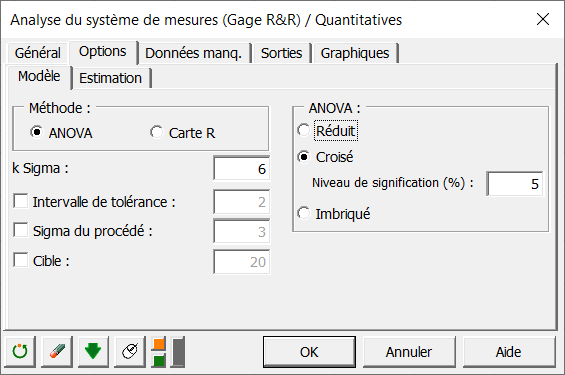
Dans l'onglet Options/Modèle, choisissez la méthode : ANOVA, entrez la valeur 6 pour le nombre de sigma utilisé pour la carte de contrôle et choisissez aussi le plan croisé pour l'ANOVA.

Dans l'onglet Options/Estimation, choisissez l’option R barre pour l’estimation de sigma.

Dans l’onglet Sorties, activez toutes les options. Faites de même dans l’onglet Graphiques.

Interpréter les résultats d'un contrôle d'une méthode de mesure avec plusieurs mesures quantitatives obtenues par plusieurs opérateurs sur plusieurs pièces

Les premiers résultats sont les composantes de la variance. La décomposition de la variance montre que la majeure partie de la variation est due à la variance entre pièces (96.40%). L'analyse du système de mesure quant à elle, n'est responsable que de 3.60% de la variance de l'échantillon. Ce système de mesure est donc capable.

Les tableaux suivants présentent les détails de la décomposition de la variance et les indicateurs d'état obtenus sur ce système. On peut voir que le ratio Signal/Bruit est adéquat.

Comme nous avons sélectionné l'option "ANOVA" nous obtenons les résultats des coefficients d'ajustement et de l'analyse de la variance. En regardant les valeurs des p-valeurs, on peut voir que tous les paramètres sont significatifs.

Après ces résultats vous trouvez les données qui permettent de construire la carte de contrôle X-barre, tout d'abord les limites de contrôle, puis les valeurs pour chaque échantillon.

Dans le premier tableau, les données de la carte de contrôle X-barre sont représentées avec les moyenne, minimum et maximum du groupe. Ensuite, la ligne centrale (CL), les limites de contrôle inférieure (LCL) et supérieure (UCL) sont affichées. Les limites inférieure et supérieure pour les opérateurs A et B sont également affichées.

La carte de contrôle X-barre résume toutes les données ci-dessus. Vous pouvez voir que les moyennes pour chaque échantillon ne sont pas dans les limites de contrôles. La variance entre les pièces n'est pas sous contrôle.

Pour la carte R, on trouve que les échantillons sont dans les limites de contrôle et aucune cause spéciale n'est détectée. Ceci est un résultat typique pour ce type d'analyse.

Les deux cartes permettent de conclure que le système de mesure est capable et que la variance entre les pièces n'est pas sous contrôle.

Vous pouvez visualiser la variance liée aux pièces et opérateurs en regardant les boîtes à moustaches et nuages de points associés à ces deux paramètres. Pour les pièces les box plots sont très serrés ce qui montre une bonne répétabilité et reproductibilité des opérateurs. Il y a clairement 3 groupes : pièces 2, 4, 6 et 8 ; pièces 3, 5, 7 et 9 ; et pièce 10.

La variance entre les opérateurs est très faible. Il n’y a pas de différences visibles.

Conclusion

Ce tutoriel permet donc de conclure que le système de mesure est capable mais que la variance entre les pièces n’est pas sous contrôle.