Taille d'échantillon et puissance pour un test de comparaison de proportions dans Excel

Ce tutoriel explique comment calculer et interpréter une taille d’échantillon et une puissance pour un test de comparaison de proportions avec Excel en utilisant XLSTAT.

Qu'est-ce que la puissance d'un test statistique ?

XLSTAT propose plusieurs tests afin de comparer des proportions. Aussi bien des tests paramétriques que des tests non paramétriques. Ainsi on peut utiliser le test z, le test du Khi², ou encore le test du signe ou celui de McNemar. XLSTAT permet également de calculer la puissance ou le nombre d'observations nécessaire pour ces tests en utilisant soit des méthodes exactes, soit des approximations.

Lorsqu'on teste une hypothèse à l'aide d'un test statistique, on a plusieurs éléments à choisir :

• L'hypothèse nulle H0 et l'hypothèse alternative Ha

• Le test statistique à utiliser

• L'erreur de première espèce (erreur de type I) que l'on appelle aussi alpha. Elle se produit lorsqu'on rejette l'hypothèse nulle alors qu'elle est vraie. Elle est fixée a priori pour chaque test et vaut 5%.

L'erreur de seconde espèce ou beta est moins étudiée mais elle revêt une grande importance. En effet, elle représente la probabilité que l'on ne rejette pas l'hypothèse nulle alors qu'elle est fausse. On ne peut pas la fixer a priori mais, on peut essayer de la minimiser, en jouant sur les autres paramètres du modèle. La puissance d'un test est calculée comme 1-beta et représente la probabilité que l'on rejette l'hypothèse nulle alors qu'elle est bien fausse.
On voudra donc maximiser la puissance du test. XLSTAT permet de calculer cette puissance (ainsi que beta) lorsque les autres paramètres du test sont connus. D'autre part, il permet pour une puissance donnée d'évaluer la taille de l'échantillon nécessaire à l'obtention de cette puissance.
Les calculs de puissance en statistique se font généralement avant que l'expérience ne soit menée. On s'en sert principalement pour estimer le nombre d'observations nécessaire pour que l'expérience ait la qualité statistique requise.

But de ce tutoriel

On souhaite comparer les proportions d’hommes et femmes sur le niveau de salaire de $50,000 à $74,999 concernant des managers travaillant dans les relations publiques aux Etats-Unis. Avant de collecter les données pour un test à 2 proportions, on utilise un calcul d'effectif d'échantillon afin d’obtenir une puissance de 0,9.

Paramétrer le calcul de la taille de l'échantillon nécessaire pour un test de comparaison de proportions

Une fois XLSTAT lancé, cliquez sur l'icône Puissance et choisissez la fonction comparer des proportions.

Une fois le bouton cliqué, la boîte de dialogue apparaît.

Vous devez alors choisir l'objectif Trouver la taille de l'échantillon, et comme test la comparaison de deux proportions (approx. De l’arcsin). On prendra comme hypothèse alternative Proportion 1 – Proportion 2 <> 0.

L'alpha est de 0,05, la puissance recherchée est de 0,9.

Comme la proportion hommes/femmes aux Etats-Unis est de 0.97, on choisi cette valeur dans le rapport N1/N2. Puis on rentre la proportion de femmes managers de 0.25 dans proportion 1 et la proportion d’hommes managers de 0.2932 dans proportion 2.

Dans l'onglet Graphique, l'option graphique de simulation est activée et on représentera la taille de l'échantillon 1 sur l'axe vertical et la puissance sur l'axe horizontal.

La puissance varie entre 0,8 et 0,95 avec un pas de 0,01.

Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués, puis les résultats sont affichés.

Interpréter les résultats du calcul de la taille de l'échantillon nécessaire pour un test de comparaison de proportions

Le premier tableau rassemble les résultats du calcul ainsi qu'une interprétation des résultats.

On voit qu'il faut 2259 observations pour l’échantillon des femmes et 2191 observations pour l’échantillon des hommes afin d’obtenir une puissance la plus proche possible de 0.9.

Le tableau suivant rassemble les calculs obtenus pour chaque valeur de la puissance comprise entre 0.8 et 0.95.

Le graphique de simulation montre l'évolution de la taille de l'échantillon en fonction de la puissance. On voit que pour une puissance de 0.8, il suffit d'un peu plus de 1688 femmes et 1637 hommes, et que pour une puissance de 0.95 on arrive à 2794 femmes et 2710 hommes.

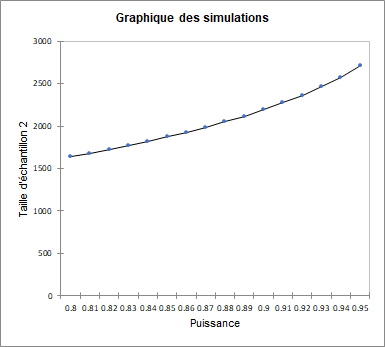
XLSTAT est un outil puissant aussi bien pour rechercher la taille de l'échantillon requise pour une analyse que pour calculer la puissance d'un test.