Análisis de Correspondencias a partir de una tabla contingencia
Este tutorial muestra cómo configurar e interpretar un Análisis Factorial de Correspondencias (AFC) en Excel usando el software estadístico XLSTAT.
¿No está seguro si este análisis multivariado de datos es la herramienta que necesita? Puede comprobarlo consultando esta guía.
Datos para ejecutar un Análisis de correspondencias
Los datos corresponden a una encuesta en la que se preguntaba a los espectadores su opinión sobre una película que acababan de ver. También se les pidió que informaran sobre su categoría de edad.
Objetivo de este tutorial
Los objetivos del análisis de correspondencias consisten en estudiar la asociación entre dos variables (filas y columnas de una tabla de contingencia) y las similaridades entre las categorías de cada variable respectivamente (filas y columnas respectivamente).
Configuración de un Análisis de correspondencias
-
Tras abrir XLSTAT, seleccione el comando XLSTAT / Análisis de datos / Análisis Factorial de correspondencias.
-
Una vez hemos hecho clic en el botón, aparece el cuadro de diálogo Análisis de correspondencias.
-
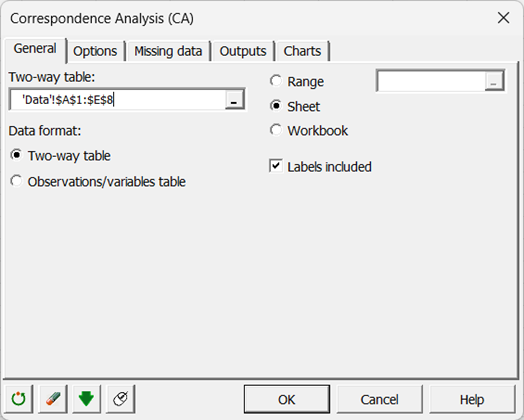
Seleccione los datos en la hoja de Excel. Si sus datos están en formato de tabla cruzada (como sucede en el ejemplo de abajo), seleccione el formato Tabla cruzada. Si sus datos están en formato Observaciones/variables, seleccione la opción correspondiente.
-
Si los nombres de las categorías para cada variable están presentes tanto en las filas como en las columnas, asegúrese de que la casilla Incluir etiquetas esté marcada.
-
No seleccione la opción Análisis no-simétrico, y elija Chi-cuadrado para la Distancia. Esta combinación de opciones permite el cálculo del análisis de correspondencias clásico (CA).
Nota: Para llevar a cabo un análisis de correspondencias no simétrico (non-symmetrical correspondence analysis, NSCA), debería seleccionar la opción Análisis no-simétrico (para lo cual únicamente está disponible la distancia chi-cuadrado). Para ejecutar un análisis de correspondencia basado en la distancia de Hellinger, no debería seleccionar la opción Análisis no-simetrico, y elegir Hellinger en Distancia.
-
En la pestaña Opciones, seleccione Ninguno en la opción Análisis avanzados.
-
En la sub-pestaña Mapas de la pestaña Gráficos, tenemos disponibles tres alternativas para graficar los resultados. La más frecuentemente usada es el mapa simétrico de filas y columnas. Para los propósitos de este tutorial, se han elegido todas las alternativas de confección de mapas.
-
En la sub-pestaña Opciones de las filas y en la sub-pestaña Opciones de las columnas de la pestaña Gráficos, seleccione la opción Elipses de confianza.
-
Haga clic en el botón OK. Aparece un cuadro de diálogo. Seleccione los ejes a mostrar en la representación gráfica del análisis de correspondencias (F1 y F2 en este tutorial) y valide la selección.
Interpretación de un Análisis de correspondencias
Antes de comenzar la interpretación, haremos una breve introducción al concepto de perfil. Ciertamente, el análisis de correspondencias se basa en el análisis de los perfiles. Un perfil es un conjunto de frecuencias dividido por el total, i.e., las frecuencias relativas. En otras palabras, un perfil refleja la forma en que la categoría de una variable cambia de acuerdo con las categorías de la otra variable.
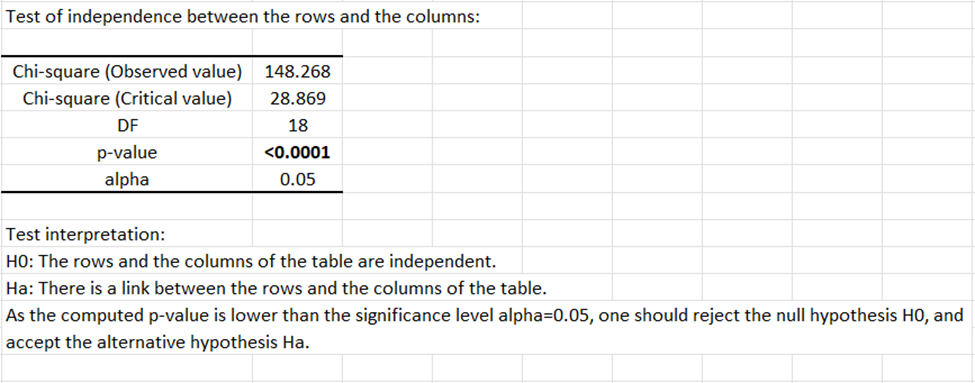
El primer resultado que se muestra es la prueba de independencia entre las filas y las columnas, basada en el estadístico chi-cuadrado. Si el valor de chi-cuadrado observado es mayor que el valor crítico, entonces el valor p estará por debajo del nivel de alfa elegido, y podremos concluir que las filas y las columnas de la tabla están significativamente asociadas. En nuestro ejemplo, es muy probable que existan diferencias entre los grupos de edad en términos de sus perfiles de apreciación.
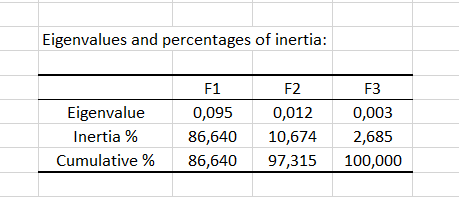
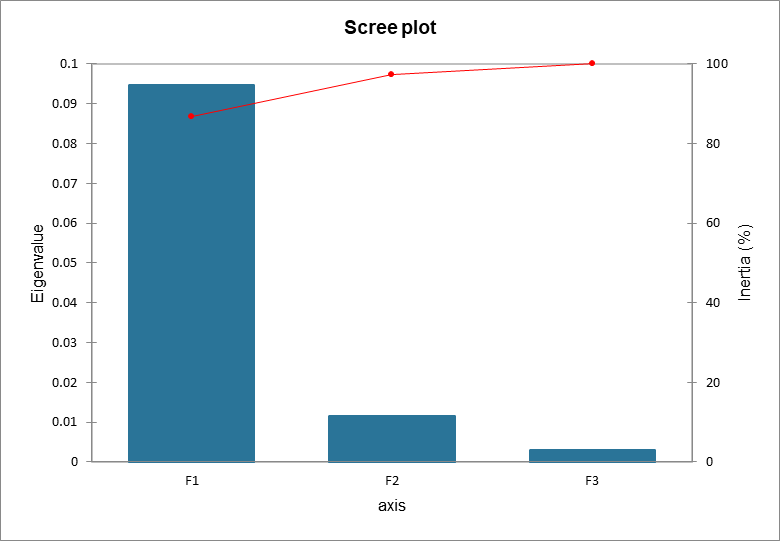
Los valores propios (eigenvalues) corresponden a la varianza extraída por cada factor (dimensión). La calidad del análisis puede evaluarse consultando la tabla de los valores propios del gráfico de sedimentación (scree plot) correspondiente. Si la suma de los dos (o unos pocos) valores propios está próxima al total representado, entonces la calidad del análisis es muy alta. El análisis de correspondencias de este ejemplo tiene una calidad elevada, toda vez que la suma de los dos primeros valores propios supone un 97% de la inercia total.
Se muestra a continuación una lista de tablas para las filas (y para las columnas, respectivamente).
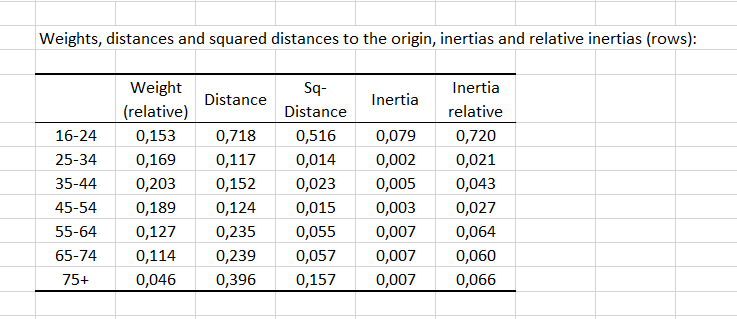
Una primera tabla muestra los pesos, las distancias y las distancias al cuadrado respecto al origen, las inercias y las inercias relativas de las filas (y de las columnas, respectivamente). Los pesos son proporciones marginales usadas para ponderar los perfiles de los puntos cuando se calculan las distancias. Mientras mayor sea la distancia al origen, más disimilitud habrá entre el perfil de la categoría y el perfil medio (es decir, más participará la categoría a la dependencia entre las dos variables). Los grupos de edad 25-34, 35-44 y 45-54 tienen la distancia más corta al origen, indicando que estos perfiles de grupo están próximos al perfil medio.
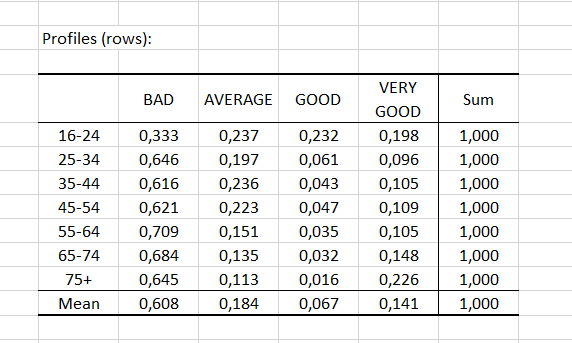
Se muestran a continuación los perfiles de fila (o de columna, respectivamente), así como el perfil medio. En nuestro ejemplo, los perfiles de los grupos de edad 25-34, 35-44 y 45-54 están próximos entre sí, y también respecto al perfil medio. Este último ha sido previsto por la corta distancia al origen.
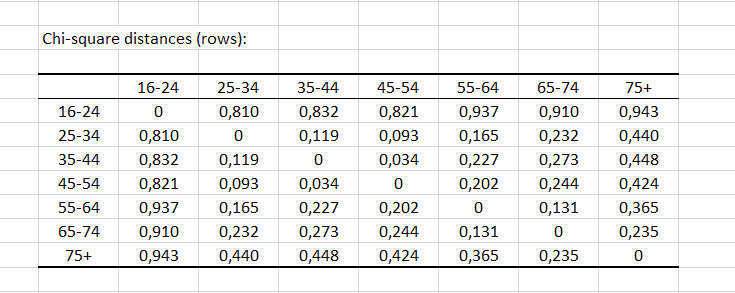
Las distancias entre las filas (y las columnas, respectivamente) proporcionan información sobre la similitud entre las categorías. Una vez más, los grupos de edad 25-44, 35-44 y 45-54 parecen ser semejantes, con una distancia por debajo de 0.2.
Se muestran a continuación las tablas de las coordenadas principales y las coordenadas estándar de las filas (y de las columnas, respectivamente). Las coordenadas estándar son las coordenadas principales divididas por la raíz cuadrada del valor propio del factor correspondiente. Las sumas de los cuadrados ponderadas de las coordenadas estándar son iguales a 1 en cada factor.
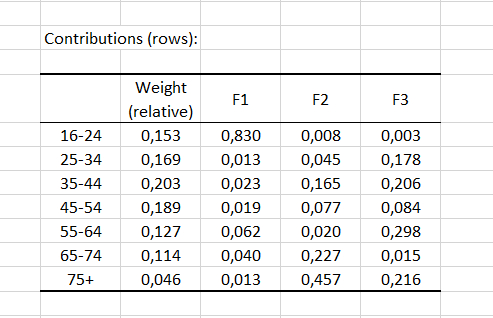
Se ofrece a continuación una tabla de las contribuciones de las filas (respectivamente, de las columnas). Las contribuciones corresponden a la importancia de cada categoría para cada factor (dimensión). La suma de las contribuciones equivale a 1 para cada factor. Como norma general, si la contribución es mayor que 1/I, siendo I el número de filas (o, respectivamente, 1/J, siendo J el número de columnas), la categoría es importante para el factor dado. En nuestro ejemplo, el grupo de 16-24 es importante para el factor F1, y los grupos 65-74 y 75+ son importantes para el factor F2.
La siguiente tabla muestra los cosenos al cuadrado de las filas (respectivamente, las columnas). Los cosenos al cuadrado representan la importancia de cada factor para cada categoría. La suma de los cosenos al cuadrado equivale a 1 para una categoría dada. En nuestro ejemplo, casi toda la varianza del grupo de 16-24 es atribuida al factor F1.
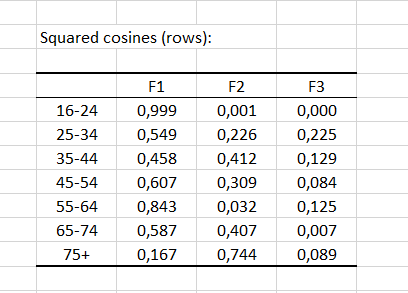
El gráfico simétrico o gráfico francés es el más frecuentemente usado. Los perfiles de fila y los perfiles de columna se superponen en una figura conjunta (ambos en coordenadas principales). Esta pantalla es muy conveniente, ya que ambos puntos de fila y de columna están igualmente repartidos. La distancia entre los puntos de fila (puntos de columna, respectivamente) se aproximan a la distancia chi-cuadrado inter-filas (respectivamente inter-columnas). Los grupos de edad 25-34, 35-44 y 45-54 están casi superpuestos en el mapa simétrico, mostrando perfiles muy similares.
La proximidad entre los puntos de fila y de columna no puede interpretarse directamente.
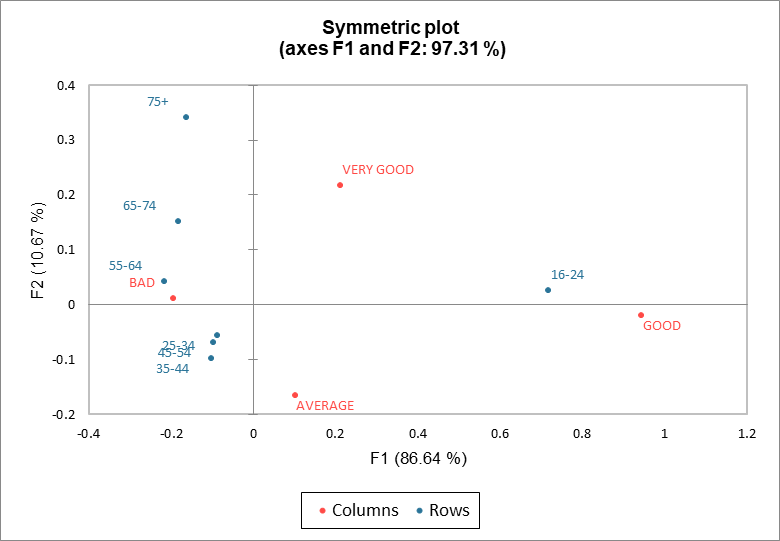
Pueden añadirse elipses de confianza a los gráficos simétricos, tal como se muestra en el gráfico de filas simétricas. Si el origen está dentro de la elipse de una categoría determinada, esta categoría no contribuye a la dependencia entre las variables. En nuestro ejemplo, las elipses confirman que los grupos 25-34, 35-44 y 45-54 no contribuyen a la dependencia entre las variables. El grupo de 16-24 contribuye a la dependencia entre las variables.
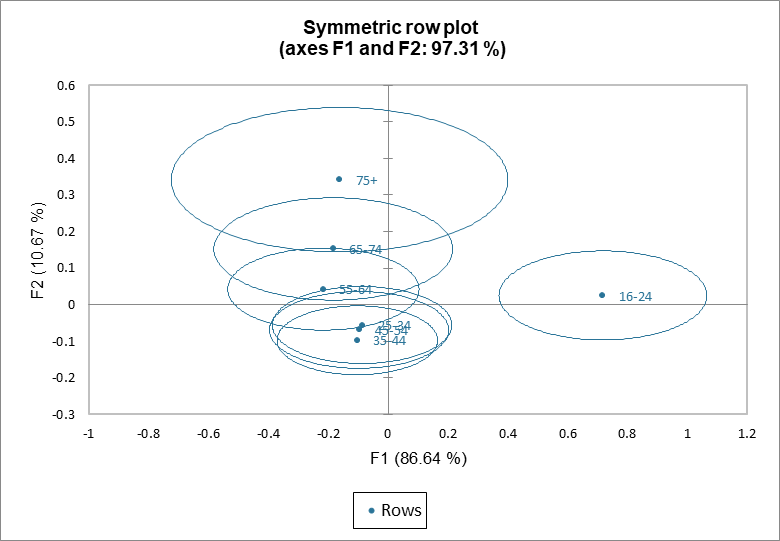
El gráfico asimétrico de filas muestra las columnas representadas en el espacio de las filas (las columnas de las coordenadas estándares y las filas de las coordenadas principales). A la inversa, el gráfico asimétrico de columnas corresponde a las filas representadas en el espacio de la columna. La distancia entre filas y columnas debe ser interpretada mediante la proyección de los puntos de fila sobre los vectores columna. El interpretar los ejes en términos de filas o de columnas depende de cuán apropiada sea la interpretación. En nuestro ejemplo, elegimos interpretar el grupo de edad en el espacio de apreciación. La primera dimensión opone bueno a malo. En el grupo de 16-24, una proporción más alta calificó el producto como bueno, comparada con las proporciones de “bueno” en los otros grupos de edad. Sin embargo, esto no significa que la calificación de “bueno” tenga la proporción más alta comparado con las demás calificaciones del grupo 16-24. Los perfiles de fila no se desvían demasiado del perfil medio (los puntos de fila están cerca del origen).
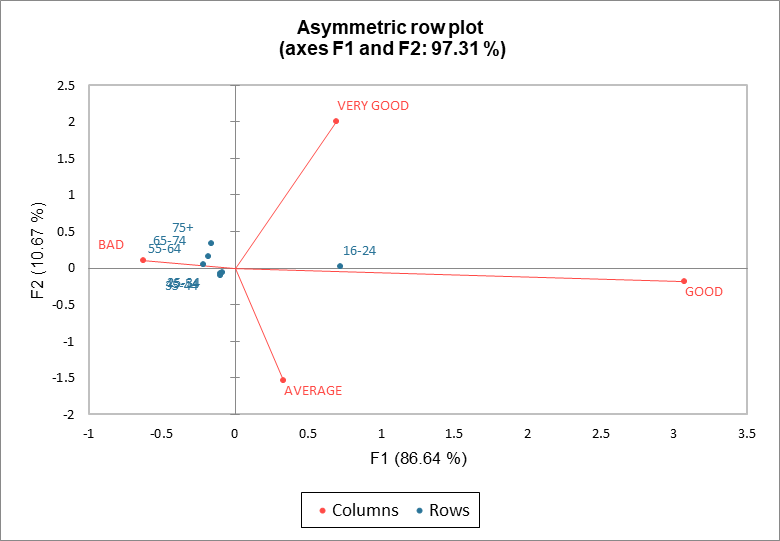
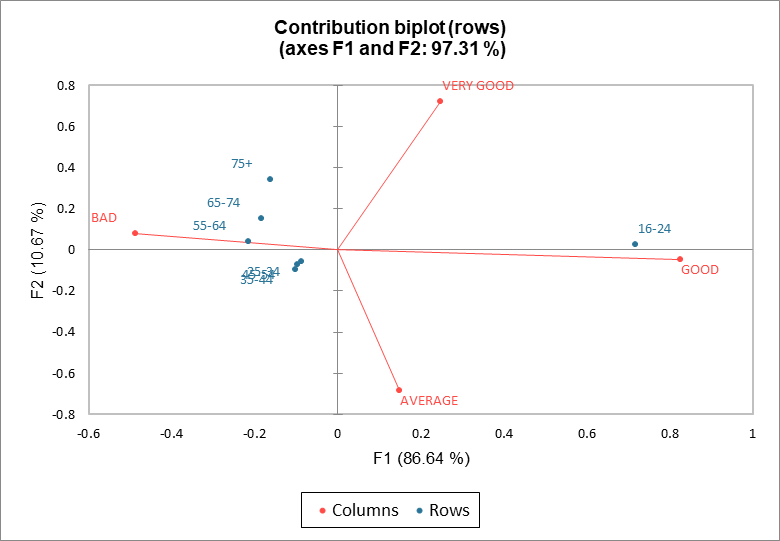
A continuación se muestra la contribución de las coordenadas de las filas y las columnas. Las coordenadas de la contribución se obtienen dividiendo las coordenadas estándar por la raíz cuadrada de la masa de una categoría dada.
En el biplot de contribución (filas), las filas están en las coordenadas de contribución y las columnas están en las coordenadas principales, e inversamente para el biplot de contribución (columnas). El biplot de contribución de filas (respectivamente, columnas), las distancias de los puntos de fila (respectivamente, de columna) al origen están relacionadas con su contribución en el mapa. En nuestro ejemplo, en el biplot de la contribución de las filas, la posición de los puntos de fila permanecen sin cambios comparados con el gráfico asimétrico. Los puntos de columna están sin embargo más cerca del origen (véanse las escalas de estos dos mapas).
El análisis de correspondencias es una técnica muy efectiva para analizar tablas de dos vías. Cuando usamos más de dos variables categóricas en una encuesta, la mejor técnica a utilizar es el análisis de correspondencias múltiples (MCA).
El siguiente video aborda la teoría del Análisis de Correspondencias (CA) y su implementación en XLSTAT.

¿Ha sido útil este artículo?
- Sí
- No