Kundenzufriedenheitsanalyse in Excel mit PLSPM
Dieses Tutorium zeigt Ihnen, wie Sie eine Kundenzufriedenheitsanalyse im Kontext einer partiellen kleinste Quadrate Pfadmodellierung (PLS-PM) in Excel mithilfe von XLSTAT durchführen.
Prinzipien des PLS Path Modeling
Die partielle kleinste Quadrate Pfadmodellierung (PLS-PM) ist ein statistischer Ansatz für die Modellierung komplexer multivariabler Beziehungen (Strukturgleichungsmodelle) unter beobachteten und latenten Variablen. Seit einigen Jahren erfreut sich dieser Ansatz wachsender Beliebtheit in verschiedenen Wissenschaften (Esposito Vinzi et al., 2007). Strukturgleichungsmodelle umfassen eine Reihe von statistischen Methodologien, die die Schätzung eines kausalen theoretischen Netzwerks aus Beziehungen ermöglichen, die latente komplexe Konzepte verbinden, von denen jedes mithilfe einer Reihe von beobachtbaren Indikatoren gemessen wird. Die erste Darstellung des abgeschlossenen PLS-Ansatzes für Pfadmodelle mit latenten Variablen wurde veröffentlicht von Wold im Jahre 1979, und die wichtigsten Verweise auf den PLS-Algorithmus stammen von Wold (1982 und 1985). Herman Wold stellte dem „hard modelling“ von LISREL (Jöreskog, 1970) (starke Verteilungsannahmen, mehrere hundert Fälle erforderlich) das PLS „soft modelling“ gegenüber (sehr wenige Verteilungsannahmen, wenige Fälle können ausreichen). Diese beiden Ansätze für das Strukturgleichungsmodell wurden in Jöreskog and Wold (1982) verglichen. Vom Standpunkt des Strukturgleichungsmodells ist der PLS-PM-Ansatz ein komponentengestützter Ansatz, bei dem das Konzept der Kausalität hinsichtlich einer linearen konditionellen Erwartung formuliert wird. Der PLS-PM-Ansatz sucht nach optimalen, linearen, prädiktiven Beziehungen anstatt nach kausalen Mechanismen und bevorzugt somit einen Prädiktions-/Relevanzorientierten Entdeckungsprozess gegenüber der statistischen Untersuchung kausaler Hypothesen. Zwei sehr wichtige Fachveröffentlichungen zum PLS-Ansatz für das Strukturgleichungsmodell sind Chin (1998, mehr anwendungsorientiert) und Tenenhaus et al. (2005, mehr theoretisch orientiert). Darüber hinaus kann PLS Path Modeling zur Analyse mehrere Tabellen verwendet werden, und stehen in direktem Zusammenhang mit klassischeren Datenanalysemethoden, die in diesem Feld verwendet werden. In der Tat können PLS-PM auch als ein sehr flexibler Ansatz für eine Multi-Block- oder (Mehrfachtabellen-)Analyse sowohl mithilfe des hierarchischen PLS Path Modeling als auch des bestätigenden PLS Path Modeling angesehen werden (Tenenhaus and Hanafi, 2007). Dieser Ansatz zeigt deutlich, wie die „datengesteuerte“ Tradition von Mehrfachtabellen-Analysen auf gewisse Weise mit der „theoriegesteuerten“ Tradition des Strukturgleichungsmodells vermischt werden kann, sodass die Analyse der Multi-Block-Daten angesichts der aktuellen Erkenntnisse über konzeptuelle Beziehungen zwischen Tabellen ermöglicht wird. In diesem Tutorium zeigen wir Ihnen Schritt für Schritt, wie Sie ein Projekt erstellen, ein Modell definieren, die Parameter schätzen und die Ergebnisse analysieren. Dieses Tutorium basiert auf der folgenden Abhandlung: [Tenenhaus M., Esposito Vinzi V., Chatelin Y.-M. and Lauro C. (2005). PLS Path Modeling. Computational Statistics & Data Analysis, 48(1), 159-205].
PLS Path Modeling mit XLSTAT-PLSPM
Datensatz für die PLS Path Modeling-Analyse
Die Anwendung basiert auf Daten aus dem echten Leben. 250 Kunden von Mobiltelefonbetreibern wurden einigen Fragen gestellt, um ihre Loyalität modellieren zu können. Das PLSPM-Modell basiert auf dem European Customer Satisfaction Index (ECSI). Im ECSI-Modell stehen die latenten Variablen (Konzepte, die nicht direkt gemessen werden können) wie nachfolgend dargestellt miteinander in Beziehung.

Jede latente Variable ist mit einer oder mehreren Manifestvariablen, die gemessen werden, verbunden. In diesem Anwendungsfall liegen die Fragen zu Manifestvariablen auf einer Skala von 0-100. Beispielsweise lauten die fünf Manifestvariablen für die latente Variable Image:
- Man kann sich drauf verlassen, was der Betreiber sagt und tut
- Er ist stabil und fest etabliert
- Er leistet einen sozialen Beitrag zur Gesellschaft
- Er ist um das Wohl der Kunden bemüht
- Er ist innovativ und vorausschauend
Ein XLSTAT-PLSPM-Projektblatt mit den Daten und Ergebnissen, die in diesem Tutorium behandelt werden, kann hier heruntergeladen werden.
XLSTAT PLSPM-Projekte sind spezielle Excel-Arbeitsmappen-Vorlagen. Beim Erstellen eines neuen Projekts beginnt der Standardname mit PLSPMBook.
Sie können die Vorlage dann unter dem gewünschten Namen speichern. Achten Sie aber darauf, den Befehl „Speichern“ oder „Speichern unter“ des XLSTAT-PLSPM-Menüs zu verwenden, um die Vorlage im Ordner, der für die PLSPM-Projekte bestimmt ist, mit der Erweiterung *.ppmx zu speichern. Des Weiteren wird beim Erstellen eines Projekts ein Dialogfenster angezeigt, in dem Sie aufgefordert werden, den Anzeigetyp auszuwählen. Im Rahmen der Zufriedenheitsanalyse verwenden wir den Modus Marketing, der die Dialogfenster und Ausgabe vereinfacht.
Hinweis: Wenn Sie die Datei PLSPathModeling_ECSI.ppmx öffnen, sieht die grafische Darstellung möglicherweise schlecht aus. Dies lässt sich auf die Tatsache zurückführen, dass die Darstellung von Ihren Bildschirmeinstellungen abhängt. Um die Anzeige zu verbessern, klicken Sie auf den Button „Optimieren der Anzeige“ (siehe unten).
Ein rohes XLSTAT-PLSPM-Projekt enthält zwei Tabellenblätter, die nicht entfernt werden können: - D1: Dieses Tabellenblatt ist leer, und Sie müssen alle Eingangsdaten, die Sie in diesem Tabellenblatt verwenden möchten, hinzufügen.
- PLSPMGraph: Dieses Tabellenblatt ist leer und wird zum Entwerfen des Modells verwendet. Wenn Sie dieses Tabellenblatt auswählen, wird das Menü „Pfadmodellierung“ oben links auf der Seite angezeigt.
Wenn Sie ein vorhandenes Projekt öffnen, kann der Anzeigemodus jederzeit durch Klicken auf die XLSTAT-PLSPM-Optionen im PLSPM-Menü geändert werden. 
In diesem Tutorium konzentrieren wir uns auf die Marketing-Anzeige, die die Verwendung von PLS Path Modeling in einer Kundenzufriedenheitsanalyse ermöglicht. Speichern Sie das Projekt mithilfe der Funktion Projekt speichern unter. Anmerkung: Sie sollten zum Öffnen und Speichern Ihrer .ppmx-Projekte immer die PLSPM-Funktionen verwenden und nicht die klassischen Excel-Funktionen.
Danach haben wir die Daten kopiert, die in der Excel-Datei verfügbar waren, und haben sie in das D1 Tabellenblatt des Projekts eingefügt. Sobald dieser Vorgang abgeschlossen ist, sind Sie bereit, mit dem Erstellen des Modells zu beginnen. Fahren Sie mit dem Tabellenblatt PLSPMGraph fort. Die Symbolleiste wird in der oberen rechten Ecke dieses Tabellenblatts angezeigt.

Um mehrere latente Variablen in einer Zeile zu erstellen, doppelklicken Sie auf den kreisförmigen Button, sodass er gedrückt bleibt, während Sie Variablen hinzufügen:

Sie können dann die Pfeile hinzufügen, die anzeigen, wie die latenten Variablen zusammenhängen. Um einen Pfeil hinzuzufügen, klicken Sie auf die latente Variable, von der er ausgehen soll, drücken Sie dann die Strg.-Taste und klicken Sie auf die latente Variable, an der der Pfeil enden soll. Dann klicken Sie auf den Pfeil-Button oder verwenden die folgende Tastenkombination: Strg+L.

Mit einer weiteren Methode können Sie vordefinierte Modelle mithilfe des siebten Buttons laden. Sie können dann das Modell aus einer Bibliothek laden, die bereits eine Liste beliebter Modelle enthält. Das ausgewählte Modell wird automatisch in das Projekt importiert. PLSPM-Projekte haben die Erweiterung .ppmxmod.
Wenn alle Pfeile hinzugefügt wurden, können Sie die Manifestvariablen definieren, die sich auf jede latente Variable beziehen (dies kann auch nach dem Hinzufügen der latenten Variablen erfolgen). Um Manifestvariablen zu einer latenten Variable hinzufügen, wählen Sie die latente Variable und klicken Sie auf den Button MV in der Symbolleiste:

Dies aktiviert das Tabellenblatt D1 und zeigt ein Dialogfenster an, in dem Sie der latenten Variablen einen Eigennamen geben, die Manifestvariablen in D1 auswählen und einige Einstellungen definieren.
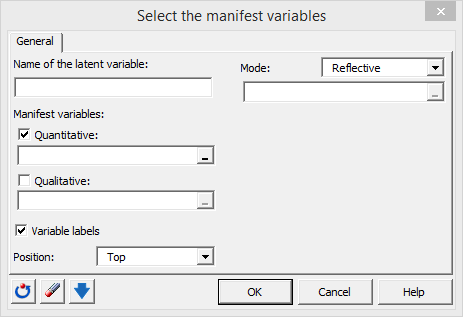
Der Modus muss definiert werden. Im Modus A (reflektiver Modus) ist die latente Variable dafür verantwortlich, was für die Manifestvariablen gemessen wird, und im Modus B (formativer Modus) konstruieren die Manifestvariablen die latente Variable. In unserem Beispiel nehmen wir an, dass unsere Manifest- und latenten Variablen mit dem Modus A verbunden sind.
Hier finden Sie die Dialogfensterkonfiguration für die latente Variable Erwartung:

Das erhaltene Modell hat die folgende Form:

Sobald die Manifestvariablen für jede latente Variable definiert wurden und die latenten Variablen verknüpft wurden, können Sie mit der Berechnung des Modells beginnen. Zum Ausführen des Modells klicken Sie auf den Button Wiedergabe.

Das Dialogfenster Start der Berechnungen erscheint, in dem viele Optionen verfügbar sind. Für dieses Tutorium wurden die folgenden Optionen verwendet:
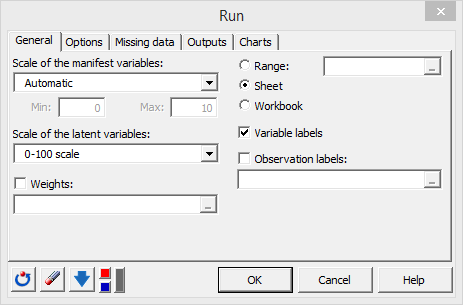
In unserem Beispiel verwenden wir den automatischen Modus für die Skalierung der Manifestvariablen und die Skalierung 0-100 für die latenten Variablen**. Lassen Sie die Standardkonfigurationen der Registerkarte Optionen unverändert. Konfigurieren Sie die Registerkarte Ausgabe wie folgt:

Aktivieren Sie die Option Simulationstabelle und wählen Sie für die zu erklärende latente Variable Zufriedenheit, weil wir die Effekte einer Veränderung der Modellvariablen auf diese spezielle Variable untersuchen möchten. Die Änderungsskala wird in Prozent gemessen und reicht von -10 % bis zu 10 % in Schritten von 1 %. Aktivieren Sie auch die IPMA-Tabelle (Important Performance Matrix Analysis).
Ergebnisse und Interpretation einer PLSPM-Projektausgabe
Der erste Teil der Ergebnisse enthält Informationen zu den Daten und zum erstellten Modell (deskriptive Statistiken in Bezug auf die Manifestvariablen und die Modellspezifikation). Zunächst ist es wichtig, Blöcke eindimensional zu untersuchen. In unserem Fall (reflektive Variablen) müssen die Blöcke eindimensional sein. Die Tabelle Blocktreue liefert diese Informationen:
 Cronbach-Alpha liegt unter dem Schwellwert von 0,7 für die Variablen Erwartung und Loyalität. Allerdings liegt das Dillon and Goldstein Rho über dem Schwellwert von 0,7 für alle Variablen. Schließlich ist der erste Eigenwert in vielen Fällen größer als der zweite. Diese Ergebnisse führen uns zu der Annahme, dass Blöcke eindimensional sind, obwohl es interessant sein könnte, zusätzliche Dimensionen in Erwartung und Loyalität zu untersuchen. Die latente Variable Beschwerde erscheint nicht in der Tabelle, da sie mit einer einzigen Manifestvariablen verbunden ist.
Cronbach-Alpha liegt unter dem Schwellwert von 0,7 für die Variablen Erwartung und Loyalität. Allerdings liegt das Dillon and Goldstein Rho über dem Schwellwert von 0,7 für alle Variablen. Schließlich ist der erste Eigenwert in vielen Fällen größer als der zweite. Diese Ergebnisse führen uns zu der Annahme, dass Blöcke eindimensional sind, obwohl es interessant sein könnte, zusätzliche Dimensionen in Erwartung und Loyalität zu untersuchen. Die latente Variable Beschwerde erscheint nicht in der Tabelle, da sie mit einer einzigen Manifestvariablen verbunden ist.
Die nächste Tabelle enthält Informationen zum Goodness of fit index.
 Der absolute GoF = 0,484. Er liegt sehr nahe an der Bootstrap-Schätzung. Dieser Wert lässt sich nicht leicht interpretieren. Er wird meist dazu verwendet, verschiedene Gruppen von Individuen oder verschiedene Modelle zu vergleichen. Der relative GoF und die GoFs basierend auf internen und externen Modellen sind sehr hoch und deuten auf eine wahrscheinlich gute Anpassung des Modells an die Daten hin.
Der absolute GoF = 0,484. Er liegt sehr nahe an der Bootstrap-Schätzung. Dieser Wert lässt sich nicht leicht interpretieren. Er wird meist dazu verwendet, verschiedene Gruppen von Individuen oder verschiedene Modelle zu vergleichen. Der relative GoF und die GoFs basierend auf internen und externen Modellen sind sehr hoch und deuten auf eine wahrscheinlich gute Anpassung des Modells an die Daten hin.
Die folgenden beiden Tabellen zeigen externe Gewichte und die mit dem Messmodell verbundenen Korrelationen an. Sobald das Messmodell untersucht wurde, kann das Strukturmodell analysiert werden. Jede latente Variable ist mit mehreren Ausgaben verbunden. Wir werden die Ausgaben der Variablen Zufriedenheit kommentieren:
 Wir können davon ausgehen, dass die latente Variable gut erklärt ist (R²=0,681). Wir sehen, dass die wahrgenommene Qualität die größte Auswirkung auf die Zufriedenheit hat, gefolgt von dem wahrgenommenen Wert. Die Auswirkung Erwartung ist nicht signifikant. Die letzte Tabelle fasst die vorhergehenden Ergebnisse zusammen. Wir sehen, dass die wahrgenommene Qualität einen Beitrag von 59 % zum R² hat.
Das folgende Diagramm veranschaulicht die soeben kommentierten Tabellen:
Wir können davon ausgehen, dass die latente Variable gut erklärt ist (R²=0,681). Wir sehen, dass die wahrgenommene Qualität die größte Auswirkung auf die Zufriedenheit hat, gefolgt von dem wahrgenommenen Wert. Die Auswirkung Erwartung ist nicht signifikant. Die letzte Tabelle fasst die vorhergehenden Ergebnisse zusammen. Wir sehen, dass die wahrgenommene Qualität einen Beitrag von 59 % zum R² hat.
Das folgende Diagramm veranschaulicht die soeben kommentierten Tabellen:
 Als nächstes werden Ausgaben in Verbindung mit der Marketinganalyse beginnend mit der IPMA (Importance Performance Matrix Analysis) angezeigt. Die IPMA ermöglicht die Visualisierung der Bedeutung und Leistung der latenten Variablen für eine Zielvariable. Hier finden Sie das Diagramm für die Variable Zufriedenheit:
Als nächstes werden Ausgaben in Verbindung mit der Marketinganalyse beginnend mit der IPMA (Importance Performance Matrix Analysis) angezeigt. Die IPMA ermöglicht die Visualisierung der Bedeutung und Leistung der latenten Variablen für eine Zielvariable. Hier finden Sie das Diagramm für die Variable Zufriedenheit:
 Wir sehen, dass die Qualität die wichtigste und leistungsstärkste latente Variable ist. Es wird schwierig werden, die Leistung der Variablen zu erhöhen, da sie bereits zu hoch ist. Es folgen die Variablen Erwartung und Image, die dieselbe Wichtigkeit haben. Image scheint interessant, da die Variable eine geringere Leistung hat und einfacher als andere Variablen verbessert werden könnte.
Dann werden die Simulationsdiagramme angezeigt. Zuerst für die Manifestvariablen:
Das erste Diagramm fasst den Effekt einer x %-igen Erhöhung einer Manifestvariablen über Zufriedenheit zusammen. Für eine Änderung von 10 % erhalten wir:
Wir sehen, dass die Qualität die wichtigste und leistungsstärkste latente Variable ist. Es wird schwierig werden, die Leistung der Variablen zu erhöhen, da sie bereits zu hoch ist. Es folgen die Variablen Erwartung und Image, die dieselbe Wichtigkeit haben. Image scheint interessant, da die Variable eine geringere Leistung hat und einfacher als andere Variablen verbessert werden könnte.
Dann werden die Simulationsdiagramme angezeigt. Zuerst für die Manifestvariablen:
Das erste Diagramm fasst den Effekt einer x %-igen Erhöhung einer Manifestvariablen über Zufriedenheit zusammen. Für eine Änderung von 10 % erhalten wir:
 Die Variable QUALITY5 hat den größten Effekt.
Die folgende Tabelle ist die gleiche wie die aktuelle, aber verwendet den Mittelwert als Grundlage.
Dann werden die Änderungen der latenten Variablen untersucht:
Die Variable QUALITY5 hat den größten Effekt.
Die folgende Tabelle ist die gleiche wie die aktuelle, aber verwendet den Mittelwert als Grundlage.
Dann werden die Änderungen der latenten Variablen untersucht:

Hier sehen wird, dass eine 10 %-ige Qualitätssteigerung zur einer 17 %-igen Steigerung der Zufriedenheit führt. Das gleiche Diagramm, basierend auf Mittelwerten, wird als nächstes angezeigt. In den entsprechenden Ausgaben finden wir die Scores der latenten Variablen sowie die damit verbundenen deskriptiven Statistiken. Die Scores können für andere Analysen in XLSTAT verwendet werden. Diese Analyse zeigte, wie ein Datensatz mithilfe eines Zufriedenheitsmodells untersucht werden kann. Wir haben die Verwendung des PLS Path Modeling-Ansatzes, mit dem Sie die Interaktionen zwischen Konzepten einfach verstehen können, veranschaulicht. Sobald das Modell bestätigt wurde, sind die Interpretation der Koeffizienten und die Ergebnisanalyse sehr einfach.
War dieser Artikel nützlich?
- Ja
- Nein