Test de racine unitaire (Dickey-Fuller) et de stationarité d'une série chronologique

Tests de racine unitaire et de stationarité

Une série temporelle Y_t (t=1,2...) est dite stationnaire (au sens faible) si ses propriétés statistiques ne varient pas dans le temps (espérance, variance, auto-corrélation). Un exemple de série temporaire stationnaire est le bruit blanc, par exemple une série où la loi de Y_t est une loi normale N(mu, sigma^2) indépendante de t. Un exemple de série non-stationnaire est la marche aléatoire. La marche aléatoire est un exemple de processus présentant une racine unitaire car elle peut être décrite par un processus auto-régressif d'ordre 1 dont le coefficient est égal à 1.

Identifier qu'une série n'est pas stationnaire permet ensuite d'étudier de quel type de non-stationnarité il s'agit. Une série non-stationnaire peut, entre autres, être stationnaire en différence : Yt n'est pas stationnaire, mais différence mais Yt - Yt-1 est stationnaire. C'est le cas de la marche aléatoire. Une série peut également être stationnaire en tendance. C'est à dire qu'elle présente une composante additive fonction du temps que l'on compensera pour ne conserver que la composante stationnaire de la série.

Les tests de stationnarité permettent de vérifier si une série est stationnaire ou non. Il y a deux types de test différents : les tests de stationnarité, comme le test KPSS, pour lesquels l'hypothèse nulle H0 est que la série est stationnaire , et les tests de racine unitaire comme le test de Dickey-Fuller, le test augmenté de Dickey-Fuller (ADF), ou encore le test de Phillips-Perron (PP) pour lesquels l'hypothèse nulle est que la série a été générée par un processus présentant une racine unitaire, et donc, qu'elle n'est pas stationnaire. XLSTAT propose le test KPSS, le test de Dickey-Fuller et sa version augmentée ainsi que le test de Phillips-Perron.

Jeu de données pour tester la racine unitaire et la stationarité d'une série chronologique

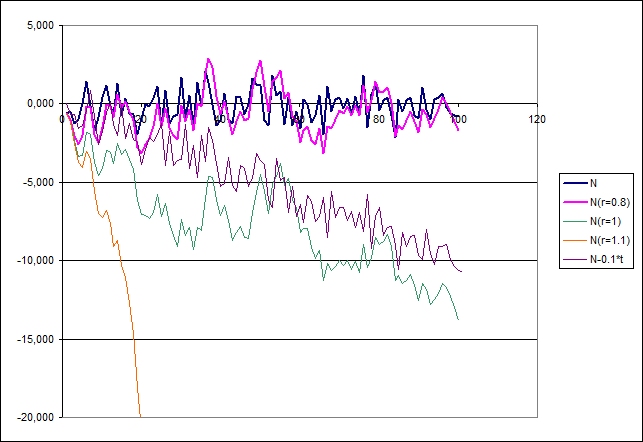
Les données ont été générées à partir d'un échantillon de 100 observations (nommée N) tirées dans une loi normale N(0, 1) - il s'agit donc d'un bruit blanc - une série stationaire crée à partir de N avec (série rho =0.8), une série autocorrélée (rho=1), une série explosive (rho=1.1), et enfin une série qui varie linéairement en fonction du temps.

Comment lancer un test ADF, PP ou KPSS sur une ou plusieurs séries temporelles?

Une fois XLSTAT lancé sous Excel, choisissez la commande XLSTAT / Time / Tests de racine unitaire et de stationnarité.

Une fois que vous avez lancer l'outil, la boîte de dialogue apparaît. Sélectionnez les données sur la feuille Excel. Dans le champ “Séries temporelles” sélectionnez les deux premières séries.

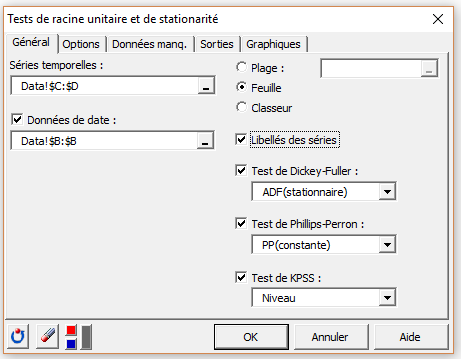
L'option "Libellés des séries" est activée parce que la première ligne des données sélectionnées contient un libellés. L'option "stationnarité" est choisie pour le test ADF, le modèle "constante" pour le test PP et le mode "Niveau" pour le test KPSS.

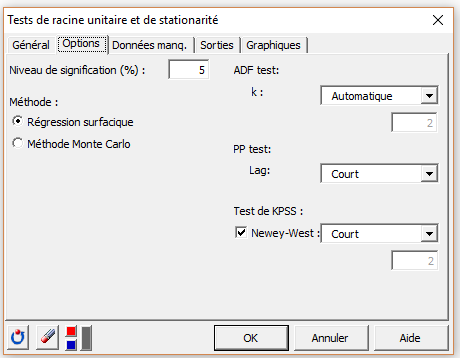
Les calculs commencent une fois que vous avez cliqué sur le bouton OK. Selon l'option sélectionnée dans l'onglet option, Régression Surfacique ou Méthode Monte Carlo, les p-values et les valeurs critiques sont calculées à partir de l'approche proposée par MacKinnon (J. G. MacKinnon, "Numerical Distribution Functions for Unit Root and Cointegration Tests", J.A.E., 1996) ou bien par un jeu de simulations Monte Carlo prédéterminé. Les résultats des tests sont ensuite affichés.

Interprétation des résultats de tests ADP, PP et KPSS (exemple sur des séries stationnaires)

Une fois affichées les statistiques descriptives des séries, les résultats des test ADF, PP et KPSS sont affichés pour la première puis pour la seconde série (voir la feuille Dickey-Fuller|Phillips-Perron1).

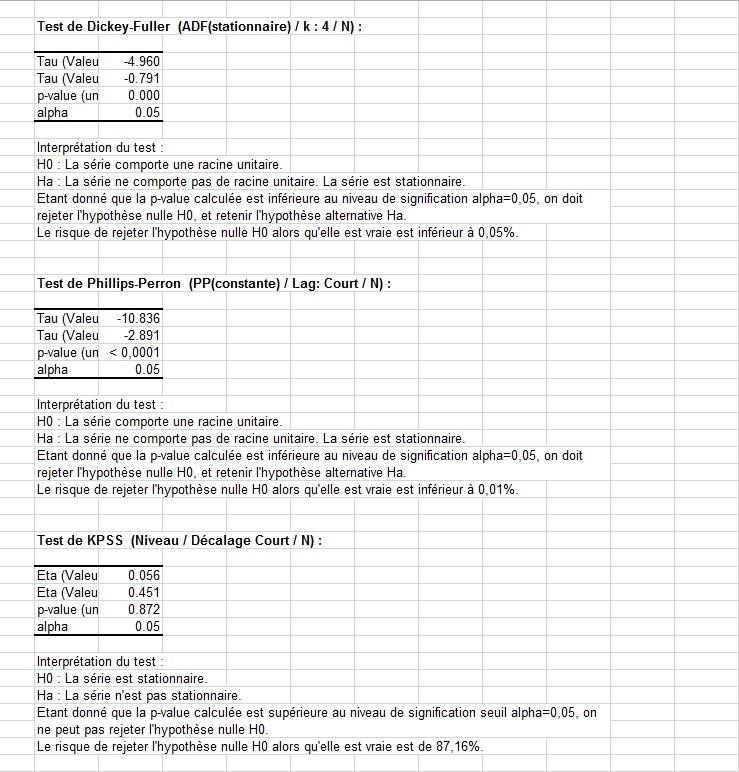
Nous pouvons voir que les deux tests se comportent de manière similaire pour ces séries. Pour la première série, les tests ADF et PP rejettent tous deux l'hypothèse nulle que la série présente une racine unitaire et retiennent l'hypothèse alternative qu'elle est stationnaire. Le test KPSS valide quant à lui l'hypothèse nulle selon laquelle la série est stationnaire.

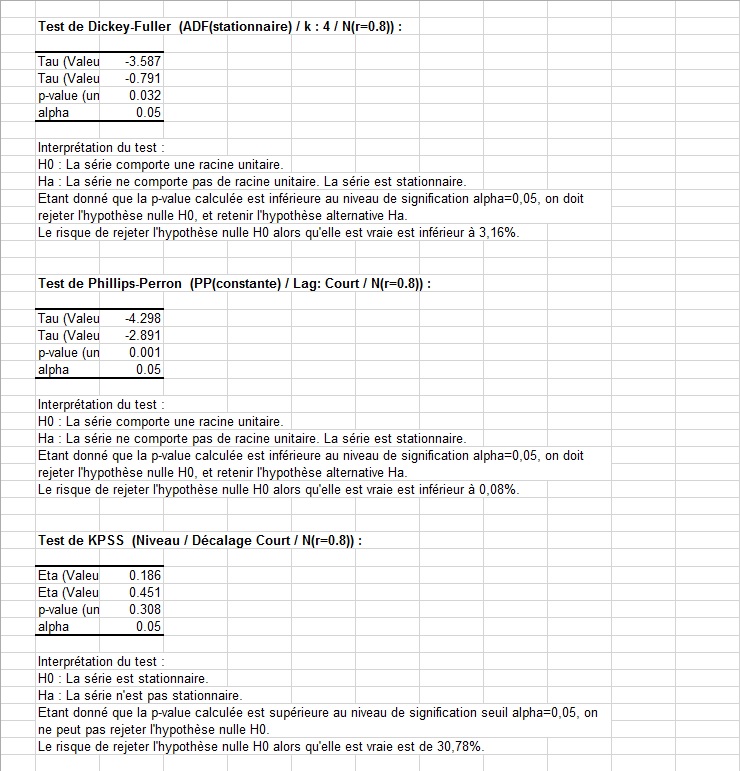
Pour la seconde série (voir les lignes 85 et suivantes), les p-values ne sont pas aussi marquées pour les 3 tests car le processus AR(1) présente une racine plus proche de l'unité (0.8).

Interprétation des résultats de tests ADP, PP et KPSS (exemple sur des séries non-stationnaires)

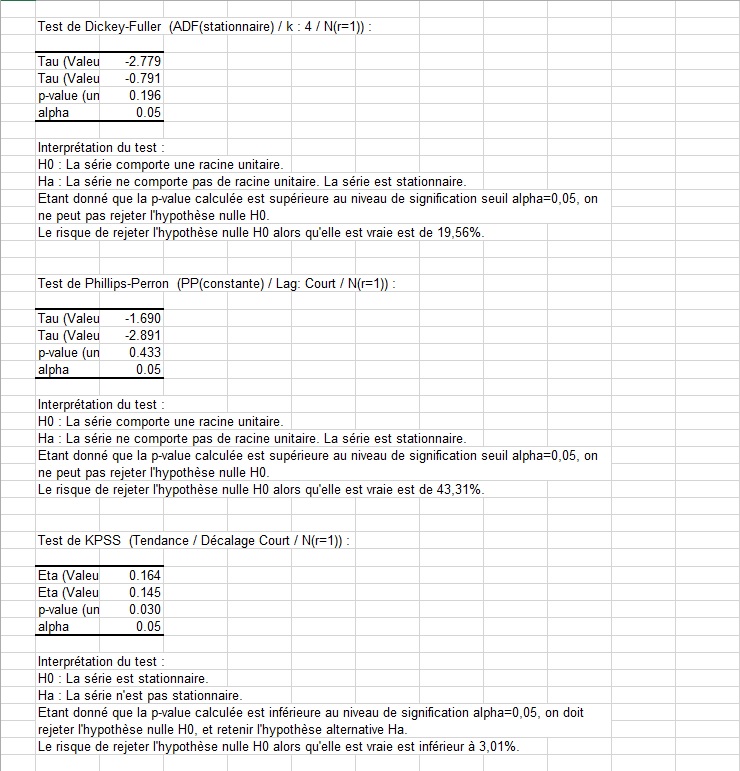
Nous effectuons ensuite les tests sur la colonne E (les résultats sont affichés dans la feuille Dickey-Fuller|Phillips-Perron2). Les tests ADF et PP ne rejettent pas le fait qu'il y ait une racine unitaire. Le test KPSS quant à lui rejette l'hypothèse nulle que la série est stationnaire. Ces deux tests fonctionnent bien sur cet échantillon.

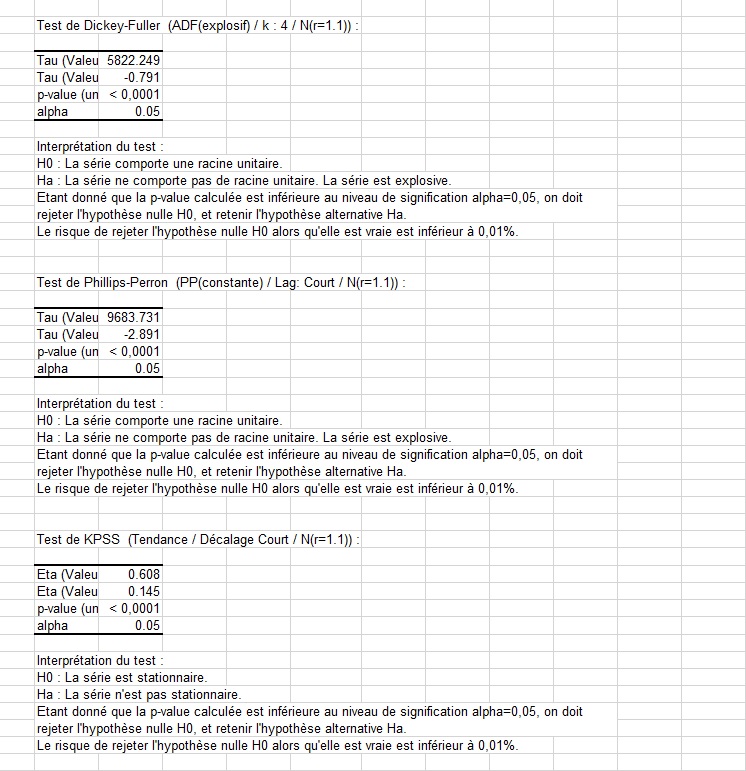
Pour la série sur la colonne F(feuille Dickey-Fuller|Phillips-Perron3), nous changeons l'option alternative à "explosif" pour le test ADF, le modèle du test PP reste le même et l'option "tendance" est choisie pour le test KPSS afin de supprimer une éventuelle tendance. Les trois tests conduisent à la conclusion que la série n'est pas stationnaire. Les résultats des 3 tests s'accordent encore une fois sur le fait que la série est effectivement stationnaire une fois la composante temporelle corrigée.

Interprétation de résultats de tests ADF, PP et KPSS (exemple avec une série variant linéairement avec le temps)

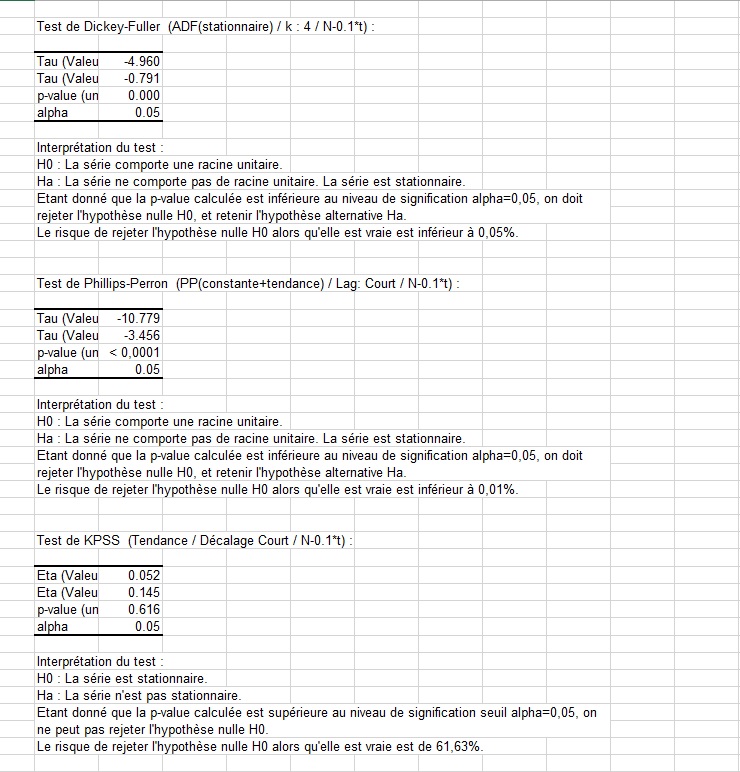
Enfin, nous lançons les tests sur la série présentant une composante fonction du temps (voir les résultats sur la feuille Dickey-Fuller|Phillips-Perron4). L'alternative choisie pour le test ADF est "stationnaire", la composante temporelle sera corrigée automatiquement lors de l'ajustement des données. Pour le test PP, le modèle retenu est cette fois-ci "constante+tendance" afin que la composante temporelle puisse être corrigée. Enfin, pour le test de KPSS nous retenons l'option "tendance".