Test du khi² et test exact de Fisher dans Excel
Ce tutoriel explique comment calculer et interpréter un test du khi² et un test exact de Fisher sur un tableau de contingence avec Excel en utilisant XLSTAT.
Jeu de données pour effectuer un test du khi² et un test exact de Fisher sur un tableau de contingence
Dans ce tutoriel nous utilisons un tableau de contingence contenant des effectifs de bananes recueillies sur un stand de marché. Le tableau croise deux variables qualitatives : variété de bananes en colonnes (3 catégories : 1, 2, 3) et présence d’asticots en lignes (2 catégories : présence, absence). Chaque cellule contient le nombre de bananes ayant la combinaison des catégories correspondantes en ligne et en colonne.

But de ce tutoriel
Le but de ce tutoriel est d’utiliser le test du Khi² et le test exact de Fisher pour tester l’association entre deux variables qualitatives mesurées sur un échantillon de bananes : variété et présence d’asticot. Plus de détails dans le paragraphe qui suit.
Quelle-est la différence entre un test du khi² et un test exact de Fisher sur un tableau de contingence ?
Conceptuellement, le test du khi² et le test exact de Fisher ont la même hypothèse nulle, et peuvent donc répondre à la même question.
H0 (hypothèse nulle) : Les deux variables qualitatives sont indépendantes. Dans notre exemple, cela voudrait dire que la présence d’asticots est indépendante de la variété de bananes. En d’autres termes, la proportion de bananes infestées est la même dans les trois variétés.
Ci-dessous une proposition d’une hypothèse alternative (bilatérale) :
Ha (hypothèse alternative) : Les deux variables qualitatives dépendent l’une de l’autre. Dans notre exemple, cela voudrait dire que la présence d’asticot dépend de la variété de bananes. En d’autres termes, au moins une des trois variétés a une proportion d’infestation différente de celle des autres.
La différence entre les deux tests est surtout une différence de manière dont la p-value est calculée.
Le test du khi² se base sur un calcul d’une statistique du khi² reflétant la distance entre le jeu de données réel et un jeu de données théorique si l’hypothèse nulle était vraie (des effectifs théoriques avec la même proportion de bananes infestées quelle que soit la variété sont alors calculés). Cette statistique est utilisée dans le cadre d’une distribution théorique du khi² pour générer une p-value. Plus la statistique du khi² est élevée, plus la p-value associée est faible. Notez qu’XLSTAT permet le calcul des effectifs théoriques (voir sections suivantes).
Le test exact de Fisher calcule la probabilité d’obtenir les données observées (en utilisant une distribution hypergéométrique) ainsi que les probabilités d’obtenir tous les jeux de données encore plus extrêmes sous l’hypothèse nulle. Ces probabilités sont utilisées pour calculer la p-value.
Lorsque l’un des effectifs théoriques est inférieur à 5 ou lorsque les sommes marginales du jeu de données réel sont très déséquilibrées, il est préférable de se fier au test exact de Fisher.
Le test du khi² a une puissance plus importante que le test exact de Fisher. En d’autres termes, il est plus apte à rejeter l’hypothèse nulle lorsqu’elle est fausse.
Paramétrer un test du khi² et un test exact de Fisher sur un tableau de contingence avec XLSTAT
Aller dans XLSTAT / tests de corrélation - d’association / tests sur les tableaux de contingence.

Dans l’onglet Général, assurez-vous d’avoir activé le format de données Tableau de contingence. Puis sélectionnez le tableau dans le champ tableau de contingence. Dans la situation où vos données sont organisées verticalement (individus en lignes et variables en colonnes), activez le format variables qualitatives. Si vous cherchez à transformer vos données d’un format vertical à un tableau de contingence, ce tutoriel vous guidera.
Dans l’onglet Options, activez les options Test du khi² et le test exact de Fisher.

Dans l’onglet Sorties, activez les options Effectifs théoriques et Proportions/ colonnes.

Cliquez sur le bouton OK pour lancer les calculs. Les résultats apparaissent dans une nouvelle feuille.
Interpréter les résultats d’un test du khi² et un test exact de Fisher sur un tableau de contingence avec XLSTAT
Tout d’abord, XLSTAT affiche les résultats associés au test du khi². La p-value (0.033) est inférieure au seuil de significativité de 0.05. Ainsi, on rejette l’hypothèse nulle que la présence d’asticots et la variété de bananes sont des variables indépendantes, en prenant un risque de 3.3% d’avoir tort.

Ensuite, les résultats relatifs au test exact de Fisher sont affichés. Là encore, la p-value (0.044) est inférieure au seuil de significativité de 0.05. Ainsi, le test exact de Fisher mène lui aussi à un rejet de l’hypothèse nulle.

Notez que la p-value obtenue via le test du khi² est légèrement inférieure à celle obtenue par la méthode du test exact de Fisher. Ceci arrive dans la majorité des cas, étant donné que le test du khi² est plus puissant que le test exact de Fisher.
Le tableau Significativité par case indique, pour chaque case, si la valeur observée est égale (=), inférieure (<) ou supérieure (>) à la valeur théorique, et pour effectuer un test exact de Fisher afin de déterminer si l'écart à la valeur théorique est significatif ou non. Les p-values du test de Fisher par case du tableau de contingence sont fournies également.
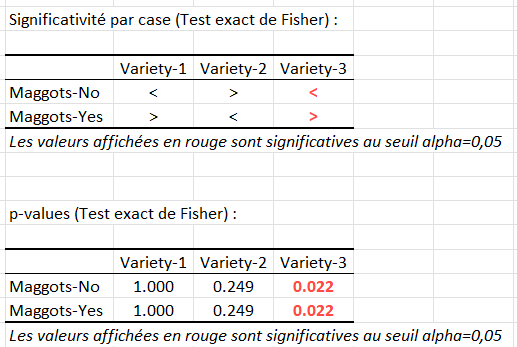
Ensuite, le tableau des effectifs théoriques contient les effectifs qui auraient été obtenus si l’hypothèse nulle était vraie. Un calcul simple montre que la proportion de bananes infestées ne change pas en fonction de la variété (11.8%). Notons que l’un des effectifs est inférieur à 5. Ainsi, nous préférons éviter de se fier à la p-value fournie par le test du khi² et de considérer uniquement la p-value associée au test exact de Fisher.

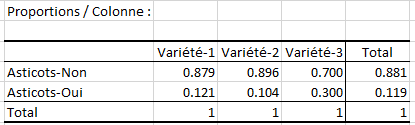
Le tableau Proportions / Colonne affiche les proportions de bananes avec / sans asticots pour chacune des trois variétés. Le résultat des tests montre qu’au moins une des proportions (0.121, 0.104 et 0.300) est significativement différente des autres.
Cet article vous a t-il été utile ?
- Oui
- Non