Graphique de Bland Altman dans Excel

Comparaison de la performance des méthodes

Lors de la mise au point d'une nouvelle méthode pour mesurer la concentration ou la quantité d'un élément (molécule, microorganisme, ...), vous pouvez vouloir vérifier si elle donne des résultats similaires à une méthode de référence ou à méthode comparable.

S'il y a une différence, il peut être intéressant de savoir si cela est dû à un biais qui dépend ou non de l'endroit où l'on se trouve sur l'échelle de variation.

Si une nouvelle méthode de mesure est moins chère qu’une méthode standard et que vous savez qu’il existe un biais, il est possible de prendre en compte ce dernier pour corriger les résultats obtenus. XLSTAT offre une série d'outils pour évaluer la performance d’une méthode par rapport à une autre.

Jeu de données pour la comparaison de méthode avec le graphique de Bland Altman

Les données correspondent à une expérience médicale au cours de laquelle la concentration d'un anticorps est mesurée sur 8 souris soumises à 8 différentes doses d'une nouvelle molécule à l'essai. Pour chaque souris, un échantillon de sang a été prélevé et divisé en quatre sous-échantillons homogènes.

Deux méthodes sont chacune testées sur 2 des 4 sous-échantillons. La première méthode est actuellement considérée comme la référence, mais elle est beaucoup plus chère que la méthode testée. Notre objectif est de vérifier s'il est possible d'utiliser la nouvelle méthode au lieu de l’actuelle.

Paramétrer une comparaison de méthode avec le graphique de Bland Altman

• Une fois XLSTAT lancé, choisissez la fonction Analyse de données de Laboratoire/Comparaison de méthodes (Bland-Altman...).

• Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données correspondant à la première puis à la seconde méthode. Comme les expériences sont répliquées, il faut préciser où se trouvent les identifiants des souris (Groupes).

• Dans l'onglet Options, nous ne sélectionnons pas l'option Difference plot car le graphique de Bland Altman est déjà un type particulier de graphique de Difference plot. Pour les autres onglets, les options sont laissées à leur valeur par défaut.

• Lorsque vous cliquez sur OK, les calculs sont effectués et les résultats sont affichés.

Interprétation des résultats de la comparaison de méthode avec le graphique de Bland Altman

Le premier tableau donne les statistiques descriptives pour les deux méthodes. La nouvelle méthode a une moyenne et une variance plus importante que la méthode de référence.

Ensuite, la répétabilité des méthodes est calculée. Pour évaluer la répétabilité d'une méthode, il faut disposer de plusieurs répétitions pour chaque mesure. Les répétitions peuvent être spécifiées en utilisant les "groupes" de la boîte de dialogue (les répétitions doivent avoir le même identifiant).

Cela correspond au cas où plusieurs mesures sont effectuées sur un échantillon donné. Si la méthode est répétable, la variance au sein des répétitions doit être faible. XLSTAT calcule la répétabilité comme la racine carrée d’une variance et fournit aussi un intervalle de confiance. Idéalement, l'intervalle de confiance devrait contenir 0.

Nous voyons ici que pour les deux méthodes les écarts-types sont faibles par rapport à l'écart-type total, mais leurs intervalles de confiance ne comprennent pas 0. Pour la 7e souris, il existe une forte différence entre les deux mesures de la méthode de référence. Cela peut être dû à une erreur de mesure ou d'un problème lié à l'échantillon. Cela devra être étudié plus avant.

Ensuite, sont affichés les résultats du test t de Student, fondé sur les moyennes des deux répétitions pour chaque souris. Ce test calcule pour chaque souris la moyenne des différences entre les deux méthodes et vérifie si elle est différente de 0 ou non. Ce test s'appuie sur l'hypothèse que les différences sont normalement distribuées. L'utilisation d'un test de normalité permet valider cette hypothèse. Toutefois, avec aussi peu de données, les conclusions des tests de normalité sont à considérer avec précaution.

Nous voyons que dans notre cas, la p-value est de 0.02, ce qui signifie que le risque de conclure que les méthodes sont différentes alors qu'elles ne seraient pas est faible. On pourrait arrêter l'analyse ici, mais nous voulons étudier plus avant la différence et non pas seulement prendre la décision sur la base d'un test qui requière des d'hypothèses importantes.

Le premier graphique permet de voir rapidement s'il y a un biais fixe ou non, en comparant directement la nouvelle méthode (ordonnées) à la méthode de référence (abscisses). Lorsque les données sont alignées sur la ligne bissectrice affichée, on se trouve dans le cas idéal où les deux méthodes donnent les mêmes résultats.

Dans notre cas, nous constatons que 5 des 8 points sont au-dessus de la bissectrice. Cela n'a rien de surprenant, mais le fait que les 3 points qui sont en-dessous soient plus proches de la ligne, nous permet de penser qu'il y a un biais positif (un biais signifie qu'il y a, par nature, une différence entre les méthodes).

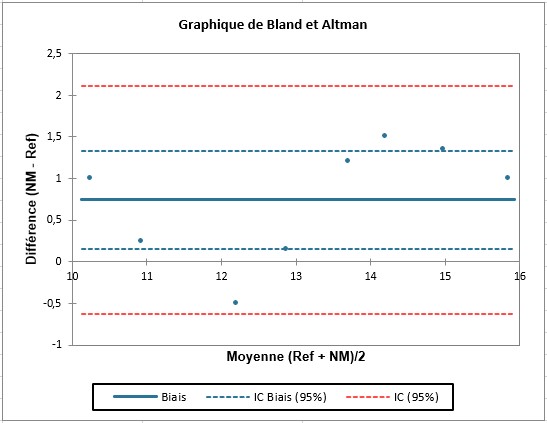
L'analyse de Bland et Altman commence par une analyse du biais. Il est ici estimé à 0.744, avec un intervalle de confiance 95% qui ne comprend pas 0. Cela confirme notre première impression.

L'intervalle de confiance sur les différences concerne les différences individuelles (le biais étant une moyenne de différences). Cela signifie que si la différence est distribuée suivant une loi normale et si le biais a la valeur que nous supposons, la différence entre deux mesures devrait se situer dans cette intervalle de confiance.

Ces résultats et les différences sont elles-mêmes affichés versus la moyenne des mesures obtenues par les deux méthodes. Nous obtenons ainsi le graphique de Bland Altman. Nous voyons ici une étrange tendance sinusoïdale qui est probablement due au hasard. Cela devra être vérifié avec de nouvelles expérimentations.

Le coefficient de corrélation de Pearson est calculé avec un intervalle de confiance afin de vérifier si la corrélation entre la différence et la moyenne est différente de 0 ou non. Sans surprise, la corrélation n'est pas significativement différente de 0, alors qu'elle ne devrait pas l'être si les méthodes étaient très proches ou si le biais était constant.

Enfin, le box plot et l'histogramme des différences sont affichés pour ceux qui veulent vérifier l'hypothèse de normalité visuellement. Bien que l'histogramme ait peu d'intérêt avec si peu de données, le box plot montre que la médiane et la moyenne sont assez éloignées les unes des autres, mais encore une fois, nous ne disposons que de peu de données ici.

En conclusion, il est très probable qu'il y ait un biais. Cela ne rend pas la nouvelle méthode non pertinente, si le biais est maîtrisé et constant sur l'échelle de variation utilisée. Cela devrait être étudié plus avant au travers d'expériences complémentaires.