Modèle à risques proportionnels avec données censurées par intervalle dans Excel

Ce tutoriel va vous montrer comment configurer et interpréter un modèle à risques proportionnels avec données censurées par intervalle dans Excel en utilisant le logiciel XLSTAT.

Modèle à risques proportionnels avec données censurées par intervalle

Ce modèle à risques proportionnels est une méthode utile lorsque l’on veut déterminer l’impact de variables explicatives sur le temps de survie d’un patient. Il s’applique à des données de survie, c’est-à-dire à des données censurées, qu’elles soient censurées à gauche, à droite, par intervalle, ou non censurées, et des variables explicatives. Ce modèle est basé sur une méthode développée par Lianming Wang, Christopher S. McMahan, Michael G. Hudgens et Zaina P. Qureshi (2016).

Le premier modèle à risques proportionnels, introduit par Cox en 1972, fonctionne avec des données non censurées et des données censurées à droite. Une autre fonction XLSTAT est dediée à ce modèle (voir ici).

Jeu de données pour la création d'un modèle à risques proportionnels avec données censurées par intervalle

Nous illustrons l’application de de modèle à risques proportionnels sur des données provenant de l’article de Jane C. Lindsey et Louise M. Ryan (Tutorial in biostatistics methods for Interval-Censored data, Statistics in Medicine, Vol. 17, No. 2, 1998, 219-238) sur la résistance à la zidovudine chez des patients subissant un traitement du SIDA.

Ces données sont compilées à partir des patients d'un site d'étude participant à quatre essais dans le AIDS Clinical Trials Group. Puisque les tests d'évaluation de la résistance aux médicaments sont coûteux, relativement peu de données sont disponibles. Sur les 31 patients ayant au moins un test, 13 sont censurés à droite (leur dernière mesure n'a montré aucune résistance à la zidovudine), 13 sont censurés à gauche (une seule mesure était disponible et était résistante), et 5 sont censurés par intervalle (une mesure a montré une sensibilité et la suivante a montré une résistance).

Les informations données par les covariables sont :

• Le stade de la maladie (précoce = 0, tardif = 1).
• La dose de zidovudine (faible = 0, élevée = 1).
• La numération lymphocytaire CD4 au départ (100-399 cellules/mm3 et >400 cellules/mm3).

Notre but est de déterminer l’impact d’un certain nombre de variables explicatives sur le temps de survie des patients.

Paramétrer un modèle à risques proportionnels avec données censurées par intervalle

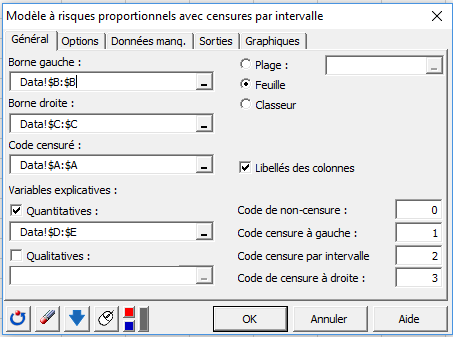
Pour activer la boîte de dialogue du modèle à risques proportionnels avec censures par intervalle, lancez XLSTAT, puis sélectionnez la commande XLSTAT / Fonctions Avancées / Analyse de survie / Modèle à risques proportionnels. Sélectionner les données de la borne gauche de l’intervalle (Left), de la borne droite de l’intervalle (Right), les données de censures (Censored), ainsi que les variables quantitatives (Stage et Dose). Les autres onglets de la boîte de dialogue permettent de paramétrer l’estimation et les sorties. Ainsi, on peut choisir ce que l’on désire utiliser afin de :

• Optimiser ou non le nombre de nœuds des splines,
• Ajouter des interactions dans le modèle,
• Paramétrer les critères de convergence,
• Supprimer ou estimer les données manquantes (il faut que les données de dates et de censure soient complètes).

Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.

Interpréter les résultats d'un modèle à risques proportionnels avec données censurées par intervalle

Des statistiques descriptives sur les variables quantitatives ainsi que sur les données censurées sont affichées : 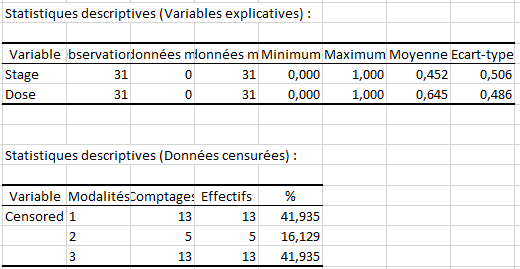Nous retrouvons bien ici les 13 données censurées à gauche, les 5 données censurées par intervalle et les 13 données censurées à droite. Le tableau suivant résume les indices de qualité du modèle. Ces statistiques sont utiles pour juger de l’adéquation d’un modèle et pour le comparer à d’autres modèles. 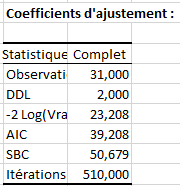En choisissant l’option d’optimisation des nœuds, on cherchera à obtenir le modèle avec le meilleur AIC (c’est-à-dire l’AIC le plus faible). Le tableau suivant est un tableau classique de modèle de régression avec, en supplément, le rapport de risque. Nous voyons que les deux variables ont un impact significatif. Elles permettent donc toutes les deux d’expliquer le temps de développement de la résistance des patients à la zidovudine. Finalement la fonction de survie cumulée est affichée en prenant en compte les variables explicatives. 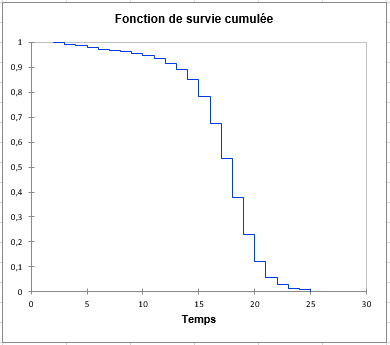Pour conclure, on peut voir que la variable stage, ayant une valeur positive, indique qu’un patient étant à un stade avancé de la maladie, aura un risque plus élevé d’être résistant à la zidovudine. Même si l’effet de la dose est moins significatif, on peut voir que le groupe ayant reçu une dose plus élevée aura aussi un risque plus élevé d’être résistant.