Analyse discriminante des composantes principales dans Excel
Ce tutoriel explique comment mettre en place et interpréter une analyse discriminante des composantes principales dans Excel avec XLSTAT-R.
L’analyse discriminante des composantes principales est une méthode multivariée qui vise à décrire des clusters et les liens existants entre eux en se basant sur des variables synthétiques ainsi qu’à exprimer la probabilité d’une observation d’appartenir à un cluster. Elle souvent utilisée pour inferer la structure genetique d'une population.
Jeu de données pour effectuer une analyse discriminante des composantes principales avec XLSTAT-R
Les données ont été prises dans le package adegenet et correspondent au premier jeu de données de dapcIllus (Jombart et al.). Il s’agit de la description d’un génotype de 600 individus qui précise le nombre (0,1 ou 2) de 140 allèles différents dans 30 localisations ainsi que le groupe (1 à 6) auquel appartient l’individu. Chaque ligne correspond à un individu (ou observation) et chaque colonne correspond à un allèle sur une localisation.
L’objectif de cette analyse discriminante des composantes principales est de décrire chaque groupe d’individus et de décrire les liens entre et au sein des groupes.
Paramétrer le calcul d’une analyse discriminante des composantes principales avec XLSTAT-R
Une fois XLSTAT lancé, cliquez sur le bouton dapc de la barre d'outils XLSTAT-R dans le package adegenet.

Une fois que vous cliquez sur la commande, la boîte de dialogue DAPC apparaît.

Dans l'onglet Général, sélectionnez vos données sur la feuille Excel. Le champ Data doit contenir toutes les données.
Le champ Groups doit contenir les groupes – la colonne EL dans notre cas qui contient le numéro du cluster auquel appartient chaque individu.
Comme nous avons sélectionné les en-têtes des colonnes, nous gardons l’option Variable labels activée. De plus, comme nous avons sélectionné les libellés des individus, nous cochons également Observation labels qui correspond à la colonne A.

Dans l'onglet Options, nous sélectionnons le nombre d’axes de l’ACP réalisée sur les données, que ce soit directement ce nombre avec Nbr of axes(PCA), ou un % de variance minimum (avec % of variance) que nous voulons expliquer. Ici, nous allons choisir le nombre d’axes nécessaire à l’explication de 70% de la variance.
Nous choisissons également le nombre d’axes ou de variables synthétiques sur lesquelles nous basons notre analyse avec Number of axes (DA).

Dans l’onglet Données manquantes, vous pouvez choisir de ne pas accepter les données manquantes, supprimer les observations ou encore d’estimer les données manquantes par la moyenne ou le mode ou encore le plus proche voisin.

Dans l’onglet Sorties, vous pouvez cocher toutes les sorties que vous souhaitez afficher. Nous choisissons ici de tout cocher pour vous décrire en détail les résultats obtenus lors de l’interprétation.

Dans l’onglet Graphiques, vous pouvez afficher seulement les individus en périphérie de chaque groupe ou encore tous les groupes avec l’arbre qui les lie.
Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.
Interpréter les résultats d’une analyse discriminante des composantes principales avec XLSTAT-R
L’analyse discriminante des composantes principales renvoie plusieurs résultats sous forme de tableaux et de graphiques.
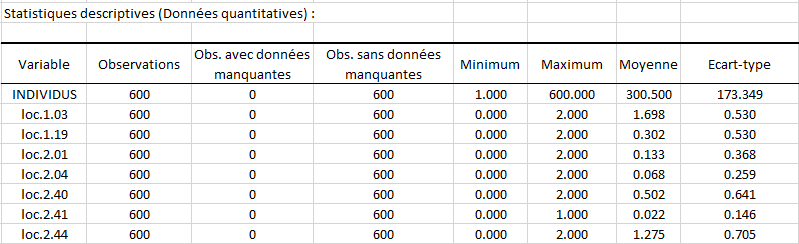
Tout d’abord, vous pouvez voir les Statistiques descriptives concernant vos données. Vous pouvez voir dans un tableau le nombre d’observations, les observations manquantes, le minimum, le maximum, la moyenne et l’écart-type pour les variables quantitatives.
Par exemple, ici il y a 600 observations concernant le nombre d’allèles 03 placés sur la localisation 1 (loc.1.03). Il y en a entre 0 et 2 à chaque observation.
Vous pouvez également voir les modalités, comptages et effectifs des variables qualitatives, ainsi que le pourcentage représenté par chaque modalité.
Par exemple, nous pouvons ici voir que les groupes sont équitablement répartis parmi les données.

Vous avez ensuite accès à toute l’information concernant la construction des variables synthétiques.
D’abord, vous avez le tableau des cinq plus grandes valeurs propres associées à chaque variable synthétique. L’inertie (ou variance) totale étant la somme des valeurs propres, nous voyons que plus une valeur propre est grande, plus elle explique une part importante de l’inertie. Ainsi, la première variable synthétique explique/représente la part la plus importante de la variance.

Ensuite, nous pouvons voir le pourcentage expliqué de la variance par l’ACP (ici, comme nous l’avions paramétré, 60%).

Par la suite, nous avons le tableau des Loadings. Pour construire les variables synthétiques de l’analyse discriminante, nous effectuons en réalité une combinaison linéaire des composantes principales de l’ACP. Ici, dans la colonne Observations nous avons donc les 35 dimensions retenues en ACP (nécessaires pour expliquer 60% de la variance) et dans les autres colonnes 35 coefficients (ou loadings) par variable synthétique (chacune correspondant à une colonne).

Ensuite, nous avons un tableau avec les coordonnées de chaque individu sur les nouveaux axes d’analyse discriminante.
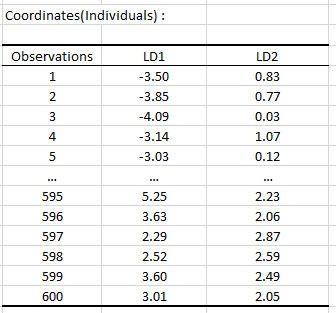
Il en est de même pour les coordonnées des six groupes.

Un tableau nous présentant les probabilités à posteriori de chaque observation d’appartenir à chaque groupe est ensuite affiché.
 Deux derniers tableaux représentant les loadings et les contributions des variables aux deux composantes d’analyse discriminante.
Deux derniers tableaux représentant les loadings et les contributions des variables aux deux composantes d’analyse discriminante.
Les loadings sont les coefficients par lesquels on multiplie les valeurs des observations afin d’avoir les axes de l’analyse discriminante.

Les contributions des variables sont des valeurs qui indiquent le pourcentage de contribution d’une variable à la construction d’un axe. Si une variable contribue fortement à un axe, cet axe représentera une évolution des valeurs de cette variable.

Enfin, deux graphiques sont représentés. Le premier indique la position des 6 clusters sur les composantes principales d’analyse discriminante. Il les relie par l’arbre minimal selon les distances au carré entre les centres des clusters. Ici, nous voyons que les clusters sont distincts dans l’ensemble mais que le 1 et le 2 (bleu et violet pâle) sont par endroits mélangés ainsi que le 5 et le 6 (orange et rouge). Le cluster 4 (jaune) est bien distinct de tous.

Le deuxième graphique indique la position des individus en périphérie de chaque cluster ainsi que leur appartenance.
 Nous pouvons voir sur le côté que ce plan est constitué des deux premières composantes d’analyse discriminante (nous avons d’ailleurs choisi de n’en garder que deux). Nous devons donc garder à l’esprit que ces représentations ne représentent fidèlement que 60% de la variance (distance entre les clusters et les individus).
Nous pouvons voir sur le côté que ce plan est constitué des deux premières composantes d’analyse discriminante (nous avons d’ailleurs choisi de n’en garder que deux). Nous devons donc garder à l’esprit que ces représentations ne représentent fidèlement que 60% de la variance (distance entre les clusters et les individus).
Conclusion
En conclusion, nous avons pu regrouper les individus dans 6 clusters selon le nombre d’allèles dans chaque locus. Ainsi, nous pouvons visualiser les individus génétiquement semblables ainsi que les variables à travers lesquelles se traduisent ces similitudes. Par exemple, la variable loc11.16 contribue à hauteur de 8% à la construction de l’axe 2 (vertical). Cela signifie que les clusters 2 et 5, situés très loin par rapport à l’axe 2, se différencient par leur nombre d’allèles sur la localisation 11.16. La représentation des individus en périphérie nous aide également à départager des individus proches de deux clusters. Les clusters 5 et 6 étant légèrement confondus, nous pouvons tout de même voir que l’individu 87 appartient au cluster 5.
Cet article vous a t-il été utile ?
- Oui
- Non