ANOVA bifactorial no balanceado con interacciones en Excel

Este tutorial le mostrará cómo configurar e interpretar un Análisis de varianza (ANOVA) bifactorial (two-way) sobre datos no balanceados en Excel usando el software XLSTAT.

¿No está seguro si esta característica de modelado es la que está buscando? Consulte por favor esta guía.

Datos para un ANOVA bifactorial no balanceado con interacciones

Descargar los datos

Los datos corresponden a una experiencia en que tres métodos de cultivo fueron probados en cuatro tipos de campos (mismo terrenos, pero con orientaciones diferentes). El rendimiento del cultivo fue medido después de la cosecha. Porque el tercer método no pudo ser probado en el cuarto tipo de campo (falta de semillas), y porque una experiencia no se pudo llevar a cabo (método 2, tipo de campo 4) a causa de una lluvia de granizos, nos encontramos aquà­ en el caso de un ANOVA desequilibrada. Como la interacción entre el método y el tipo de campo es interesante para el investigador, realizaremos aquà­ un ANOVA con interacciones.

Utilizando la herramienta del ANOVA de XLSTAT, aquà­ buscamos determinar si existe una influencia significativa de método, del tipo de campo, y eventualmente de su interacción.

Configuración de un ANOVA bifactorial no balanceado con interacciones

Una vez XLSTAT iniciado, elija el comando XLSTAT / Modelización de datos / ANOVA.

Una vez el botón pulsado, aparece el cuadro de diálogo correspondiente al ANOVA.

Puede elegir entonces los datos en la hoja Excel.

La "Variable a modelizar" corresponde a la variable explicada, es decir en este caso preciso, al rendimiento del cultivo del que queremos explicar la variabilidad por el efecto del método, del tipo de campo y del metodo*tipo de campo (la interacción).

La opción "Referencias presentes" se deja activada porque la primera là­nea de columnas incluye el nombre de las variables. Dejamos seleccionada la opción "Residuos" ya que analizaremos los residuos para validar las hipótesis de normalidad del ANOVA, e identiicar valores extremos.

En XLSTAT, es posible seleccionar los datos de dos maneras diferentes para el ANOVA. La primera se presenta en forma de columnas, una columna para la variable dependiente y otra para la variable explicativa.

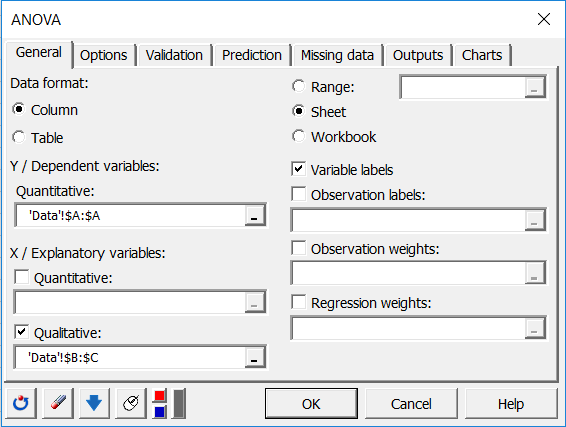
La segunda forma de seleccionar los datos es en forma de tabla, donde cada columna representa una modalidad de la variable explicativa.

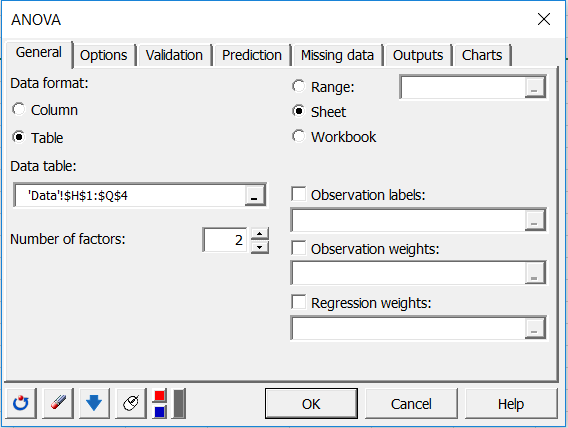En la ficha Opciones, la opción Interacción está activada y el nivel máximo de interacción está establecido en 2.

Dejamos la restricción a "a1=0", lo que implica que el modelo se escribirá de manera a tener en cuenta que el método 1 y el tipo de campo tendrán el efecto de base.

Aplicar una restricción en ANOVA es indispensable por razones teóricas, pero eso no cambia los resultados (previsiones, R2, etc.), ni la calidad del análisis.

En la pestaña Resultados se activaron las opciones de Tipo SS porque queremos que el modelo tenga en cuenta las interacciones, y porque queremos analizar los valores de F dados en las tablas de Tipo I SS, y Tipo III SS (SS significa suma de cuadrados).

Una vez que haya pulsado el botón OK, los cálculos son efectuados, y los resultados son visualizados.

A continuación, se mostrarán los resultados.

Interpretación de los resultados de un ANOVA bifactorial no balanceado con interacciones

El primer cuadro de resultados proporciona los coeficientes de ajuste del modelo. El R2 (coeficiente de determinación) proporciona una idea del % de variabilidad de la variable a modelizar, explicado por las variables explicativas. Mientras más cerca de 1está este coeficiente, mejor es el modelo. En nuestro caso, 92% de la variabilidad es explicado por el método, el tipo de campo y la interacción. El resto de la variabilidad es explicable por efectos que no fueron identificados en curso de esta experiencia. Se encuentran incluidos entonces en la parte "aleatorio" del modelo.

El cuadro de análisis de la varianza es un resultado que debe ser atentamente analizado (ver a continuación). Es en este nivel que comprobamos si podemos considerar que las variables explicativas seleccionadas y sus eventuales interacciones originan una cantidad de información significativa al modelo (hipótesis nulo H0) o no. En otros términos, es una manera de probar si la media de la variable a modelizar bastarà­a con describir los resultados obtenidos o no.

La prueba del F de Fisher es utilizada. Dado que la probabilidad asociada al F es, en este caso, de 0.0003, significa que nos arriesgamos el 0.03% concluyendo que la variable explicativa origina una cantidad de información significativa al modelo. Se puede deducir entonces que las dos variables y sus interacciones originan una información significativa para explicar la variabilidad del rendimiento. Queremos ahora saber si las variables contribuyen también a explicar la variabilidad. Para eso analizaremos los cuadros de resultados Tipo I SS y Tipo III SS.

El cuadro Tipo I SS es elaborado añadiendo las variables una por una en el modelo, y evaluando el impacto sobre la suma de los cuadrados del modelo. Por este motivo, el orden en el cual las variables son introducidas en el modelo influye sobre los resultados obtenidos. El cuadro Tipo III SS es calculado suprimiendo puntualmente cada una de las variables del modelo, todas las otras siendo presentes, con el fin de evaluar el impacto de la variable eliminada sobre el modelo. Asà­, los valores obtenidos en el cuadro Tipo III SS son independientes del orden en el cual son seleccionadas las variables. El cuadro Tipo III SS es frecuentemente preferido para el análisis de los resultados de un modelo con interacciones.

Comentario : la suma de los cuadrados del Modelo es más elevada, la suma de los cuadrados de los Residuos es más escasa, y la influencia de la variable sobre el modelo es más importante.

De los resultados del cuadro Tipo III SS, podemos deducir que el método es la variable que proporciona más información al modelo. Analizando los parámetros del modelo (ver a continuación) notamos que los métodos 2 y 3 tienen un efecto positivo sobre el rendimiento. El tipo de campo carece de efecto significativo sobre el modelo, la interacción entre esta variable y el método tiene un efecto significativo (al umbral de 5%). Para los próximos análisis, las dos variables principales deberán entonces ser conservadas.

El cuadro más arriba puede ser utilizado para estudiar el impacto de las variables en el rendimiento, pero para prever también valores en situaciones que no fueron encontrados. Asà­, según el modelo, podemos determinar que el método 3 aplicado en un tipo de campo 4, originarà­a un rendimiento medio de 48.5, sabiendo que la influencia de la interacción entre el método 4 y el tipo de campo 3 no se puede tener en cuenta.

Por último, los residuos centrados reducidos deben tener una atención particular, dado que las hipótesis vinculadas al ANOVA, deben ser distribuidos según una ley normal N(0,1). Eso significa, entre otros, que 95% de los residuos deben encontrarse en el intervalo [-1.96, 1.96]. Dado que el escaso número de datos del que disponemos aquà­, cualquier valor fuera de este intervalo es revelador de un dato sospechoso. Podemos verificar aquà­ que todos los datos están en el intervalo.