Comparaciones múltiples pairwise ANOVA multifactorial

Este tutorial le ayudará a entender mejor los procedimientos de comparaciones múltiples, con una aplicación al contexto del Análisis de Varianza (ANOVA) en Excel usando el software XLSTAT.

Datos para ejecutar comparaciones múltiples por pares tras un ANOVA multifactorial

Descargar los datos

Los datos corresponden a una prueba sensorial sobre dos productos alimenticios. Cuatro evaluadores han probado ambos productos y han dado calificaciones sobre dos características: la calidad y la dulzura. Cada producto ha sido probado seis veces por cada juez dentro de diferentes sesiones de prueba. Los datos se han generado artificialmente.

Objetivo de este tutorial

El objetivo de este tutorial se focaliza en las comparaciones múltiples por pares (multiple pairwise comparisons), también denominadas comparaciones post hoc, y que habitualmente se ejecutan mediante pruebas paramétricas y no paramétricas. Investigamos este problema con un ejemplo sofisticado que implica dos ANOVAs bifactoriales incluyendo la interacción estadística Juez x Producto. En el caso de ser significativa, esta interacción reflejaría diferencias contrastadas entre las calificaciones de los dos productos a través de los jueces. Por ejemplo, algunos jueces han calificado al producto A mejor que al B, en tanto que otros han calificado mejor el producto B que el A. El llevar a cabo comparaciones múltiples por pares en el nivel de la integración podría ayudarnos a identificar con precisión qué juez pertenece al primer grupo y qué juez pertenece al segundo.

Unas palabras sobre las herramientas de comparaciones múltiples

Tras detectar que un factor tiene un efecto significativo globalmente sobre una variable dependiente, con frecuencia deseamos ir más allá en los detalles y preguntar qué niveles específicos del factor difieren de uno al otro. Por ejemplo, podríamos comprobar los efectos de un factor que implique 4 tratamientos sobre la presión sanguínea. Ejecutar un ANOVA unifactorial sobre los datos respondería a la pregunta muy general “¿Hay al menos un tratamiento que sea significativamente diferente de los demás?” Si la prueba ANOVA es significativa, podríamos hacer otra pregunta: “¿Qué tratamientos difieren unos de otros?” Responder esta pregunta requiere comprobar las diferencias entre todos los pares de tratamientos. Las herramientas de comparaciones múltiples por pares se han desarrollado para afrontar este tipo de problemas.

Las herramientas de comparaciones múltiples por pares normalmente implican el cálculo de un valor p para cada par de niveles calculados. El valor p representa el riesgo que asumimos cuando estamos equivocados al establecer que el efecto es estadísticamente significativo. Mientas más alto sea el número de pares que deseamos comparar, mayor será el número de valores p calculados, y consiguientemente el riesgo de detectar efectos significativos que no lo son en realidad. Considerando un nivel de significación alfa del 5%, encontraríamos 5 valores p significativos por azar sobre 100 efectos investigados que no son significativos en realidad. Por consiguiente, las herramientas de comparaciones múltiples por pares implican correcciones del valor p: los valores p son penalizados (esto es, aumentados) conforme aumenta su número.

La elección de pares de niveles factoriales a comparar depende de la pregunta que nos hagamos y, por tanto, debería hacerse en el momento de planificación del estudio. Ciertamente, con frecuencia estamos interesados en comparar todos los niveles entre sí. Teniendo en cuenta esta perspectiva, XLSTAT proporciona diferentes métodos incluyendo el procedimiento HSD de Tukey (Tukey Honest significant difference), que es, junto con el LSD de Fisher, uno de los procedimientos más frecuentemente usados en comparaciones múltiples por pares. También es conocido el método de Newman-Keuls SNK (disponible en XLSTAT), si bien no es demasiado fiable debido a su carácter débilmente conservador. El método REGWQ se encuentra entre las pruebas más fiables, pese a que su uso no está demasiado extendido.

En otras sutuaciones, únicamente nos interesa comparar todos los niveles con un control. Seleccionando este subconjunto de pares decrece el número de valores p calculados y, en consecuencia, su penalización. En ese caso, hablamos de los contrastes de Dunnett, que también están disponibles en XLSTAT. Se pueden especificar pares más personalizados a través de comparaciones múltiples tras un ANOVA unifactorial en XLSTAT.

Ejecución de comparaciones múltiples por pares tras ANOVAs bifactoriales

Ejecutaremos ahora comparaciones múltiples por pares tras ANOVAS bifactoriales incluyendo una interacción entre los factores.

Abra el menú XLSTAT y haga clic en XLSTAT / Modelado de datos / ANOVA.

En la pestaña General, seleccione las columnas Taste y Sweetness como variables dependientes, y las columnas Panelist y Product como variables cuantitativas explicativas. En la pestaña Opciones, active la opción Interacciones / Niveles, y seleccione interacciones de nivel 2, de forma que se tome en cuenta la interacción estadística Panelista x Producto. En la pestaña Resultados / General, asegúrese de activar la opción Tipo I/II/III SS.

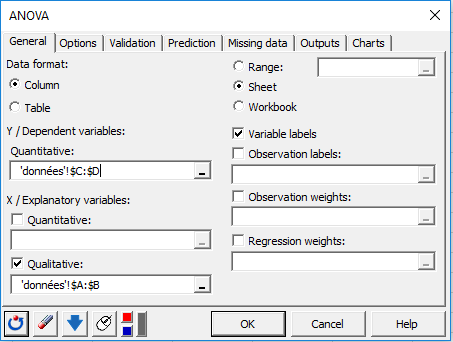
En la pestaña Comparaciones múltiples, active la opción comparaciones por pares, y elija luego Tukey HSD. Activando las opciones de errores estándar e intervalos de confianza en esta pestaña, calcularemos esas características en torno a las medias y las mostraremos en los resultados. El no activar la opción “Aplicar a todos los factores” le permitirá elegir los factores del modelo y/o las interacciones sobre las que desea llevar a cabo las comparaciones múltiples. Haga clic en el botón OK.

Tras hacer clic en el botón, aparecen sucesivamente tres cuadros de diálogo. En el primero, debería definir qué conjunto de factores y de interacciones desea incluir en los modelos ANOVA generales. En los dos siguientes, debería definir el conjunto de factores e interacciones sobre los que desea llevar a cabo comparaciones múltiples por pares para cda una de las dos variables dependientes. Seleccione los tres elementos de la lista (dos factores y una interacción) en cada uno de los tres cuadros de diálogo. Los resultados aparecen a continuación en una nueva hoja de Excel.

Interpretación de comparaciones múltiples por pares tras ANOVAs bifactoriales

Para la variable Taste, las tres tablas ANOVA de suma de cuadrados son exactamente las mismas. Esto sucede cuando el diseño experimental es balanceado. Si fuera no balanceado, la tabla de suma de cuadrados Tipo III sría la más fiable (puede echar un vistgazo a este tutorial). Pese a que el efecto del producto sobre el gusto no es significativo al nivel de 0.05 (p = 0.334), la interacción estadística Panelist x Product es muy significativa (p < 0.0001).

La interpretación de este patrón puede llevarse a cabo con facilidad usando el gráfico de medias situado en la parte inferior derecha: pese a que por término medio ambos productos están calificados casi lo mismo en la escala de gusto (en torno a 5.5), los jueces parecen tyener puntos de vista muy contrastados. En tanto que los jueces 1 y 2 prefieren fuertemente el producto A sobre el producto B, los jueces 3 y 4 prefieren el producto B al producto A. Es más, todos los jueces parecen estar de acuerdo sobre el grado de gusto promedio del producto B.

Pongamos ahora nuestra atención sobre la sección de comparaciones múltiples por pares. Cada factor o interacción tiene su propia subsección. Para el factor juez, todos los jueces se comparan unos con otros independientemente del producto. Para el factor producto, ambos productos se comparan sin tener en cuenta a los jueces. Para la interacción Juez x Producto, se comparan unas con otras todas las combinaciones de niveles entre los dos factores. Normalmente, resulta de interés prestar atención a los factores o interacciones que son más significativas de acuerdo a la tabla ANOVA. Esta es la razón por la que vamos a examinar con más detalle el término de interacción para la variable gusto.

En primer lugar, se muestra una tabla que contiene información extensa como las diferencias entre las medias y los valores p de cada par.

La información significativa que emerge de esta tabla se resume en una tabla más pequeña más abajo, donde todas las combinaciones entre los niveles de los dos factores están asociados a letras. Centraremos nuestra atención en esta segunda tabla para su interpretación.

Dos combinaciones de niveles que compartan la misma letra no son significativamente diferentes. Dos combinaciones sin letras en común son significativamente diferentes.

En términos globales, las conclusiones que extrajimos del gráfico de medias gozan de apoyo estadíticos por las tablas de comparaciones múltiples por pares.

En las combinaciones que incluyen el producto A (primeras dos líneas y últimas dos líneas de la tabla), los jueces 1 y 2 comparten la misma letra (A) y no tienen ninguna letra en común con los jueces 3 y 4, quienes comparten la misma letra (C). Esto significa que los dos grupos de jueces no están de acuerdo respecto al producto A. En las combinaciones que incluyen el producto B (las cuatro líneas centrales de la tabla) vemos que todas las combinaciones comparten la letra B. Esto significa que todos los jueces están de acuerdo en el gusto del producto B.

Desde una perspectiva de marketing, sería interesante tomar como objetivo a consumidores que tienen perfiles similares a los jueces 1 y 2 cuando se haga publicidad del producto A. Por otra parte, el producto B requeriría una mejora en el sabor antes de considerar ponerlo en el mercado.

En lo que atañe a la variable dependiente dulzura, las tablas ANOVA muestran un efecto muy significativo del producto (p < 0.0001) y efectos no significativos de Panelist (p = 0.704) y de la interacción (p = 0.427).

El gráfico de medias de la parte inferior derecha muestra que todos los jueces están de acuerdo en el hecho de que el producto B es más dulce que el producto A.

Resultaría irrelevante examinar aquí la sección de comparaciones múltiples, toda vez que el único elemento significativo del modelo (i.e., el factor producto) contiene únicamente dos niveles, que necesariamente deberán ser diferentes tal como quedó sugerido en las tablas ANOVA.

Interpretación de gráficos de medias LS

Hemos sometido a prueba los efectos interactivos de jueces y productos sobre las variables dependientes sabor y dulzura. XLSTAT proporciona la herramienta de medias LS, que resulta útil para comparar los efectos del mismo conjunto de factores e interacciones sobre diferentes variables dependientes.

Una tabla resumen de medias LS, así como un gráfico de medias LS, están asociados a cada factor e interación.

En el caso del factor juez, la tabla resumen de medias LS muestra las estimaciones de la calificación media otorgada por cada juez a cada una de las dos variables dependientes. Advierta que dentro de cada variable dependiente se han introducido letras de significación de comparación múltiple por pares como comentarios dentro de las celdas que contienen las estimaciones de las medias. Para mostrar la(s) letra(s) asociadas a una media específica, simplemente mueva el cursor del ratón hasta el triángulo rojo de la esquina superior derecha de la celda correspondiente.

El gráfico muestra que, independientemente de los productos, los jueces están en desacuerdo principalmente en el gusto, pero concuerdan en la dulzura, resultado que tiene apoyo en los valores p asociados a los efectos del juez en ambos modelos ANOVA.

El gráfico de medias LS de los productos muestra que, independientemente del juez, los productos son calificados de la misma forma en la escala de sabor, en tanto que son juzgados como diferentes en la escala de dulzura.

No vamos a analizar el gráfico de interacción de medias LS porque es demasiado confuso.