F-Test zum Vergleich zweier Varianzen in Excel
Dieses Tutorium wird Ihnen helfen, die Differenz zwischen zwei beobachteten Varianzen mithilfe des Fisher F-Tests in Excel mithilfe der Software XLSTAT zu testen. Sie sind sich nicht sicher, ob dies der statistische Test ist, nach dem Sie suchen? Weitere Hinweise finden Sie hier.
Datensatz für die Durchführung eines Fisher F-Tests in XLSTAT zur Bewertung der Gleichheit einer Varianz von 2 Stichproben
Absicht dieses Tutoriums
Unsere Absicht besteht darin, zu bewerten, ob eine Differenz zwischen den Spezies bei der Länge und Breite der Blütenblätter besteht. Wir vergleichen danach die Verteilung dieser Variablen für die 2 Stichproben.
Testen der Normalität der Stichproben
Als erstes muss bewertet werden, ob die Stichproben einer Normalverteilung folgen, da der Fisher F-Test sensitiv für Daten ist, die keiner Normalverteilung folgen. Sie finden die Berechnung dieser Statistiken in dem Excel-Tabellenblatt. Alle 4 Stichproben (Länge der Blütenblätter Versicolor, Breite der Blütenblätter Versicolor, Länge der Blütenblätter Setosa, Breite der Blütenblätter Setosa) folgen einer Normalverteilung.
Erstellen eines Fisher F-Tests in XLSTAT zur Bewertung der Gleichheit einer Varianz von 2 Stichproben
Danach führen wir einen F-Test durch, um herauszufinden, ob die Varianzen gleich sind. Wenn die Varianzen gleich sind, können wir einen Test durchführen, um die Mittelwerte zu vergleichen. Um einen Vergleich der Varianzen von zwei Stichproben durchzuführen, gehen Sie zur Menüleiste Parametrische Tests/Vergleich der Varianzen von zwei Stichproben.

Im Dialogfenster Vergleich der Varianzen von zwei Stichproben in der Registerkarte Allgemein markieren Sie die Daten für die Stichprobe 1 und 2. Für Stichprobe 1 wählen Sie die Spalte B, die die Länge der Blütenblätter für die Art Versicolor enthält, aus und für Stichprobe 2 die Spalte E entsprechend der Länge der Blütenblättern für die Setosa-Stichproben.
Das Datenformat ist Eine Spalte pro Stichprobe, da jede Spalte einer der Stichproben entspricht.
Wir wählen die Option Tabellenblatt, um die Ergebnisse in einem neuen Blatt der Arbeitsmappe zu erhalten.
Da die Spalten einen Namen haben, muss die Option Beschriftung der Spalten aktiviert sein.
Der Test, den wir durchführen möchten, ist der Fisher-F-Test.

Sobald alle diese Optionen eingestellt sind, können wir zur Registerkarte Optionen wechseln.
Wir möchten die Gleichheit der Varianz testen, was bedeutet, dass wir die Alternativhypothese testen müssen: Varianz 1 / Varianz 2 ≠ R wobei R = 1.
Das Standardsignifikanzniveau von 5 % soll beibehalten werden.
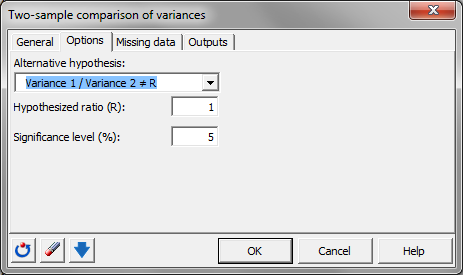
Wir haben keine fehlenden Daten, daher können wir direkt zur Registerkarte Ausgabe gehen und die einzige verfügbare Option aktivieren: Deskriptive Statistiken.

Wenn alles eingestellt ist, klicken Sie auf OK.
Ergebnisse eines Fisher-F-Tests in XLSTAT zur Bewertung der Gleichheit der Varianz von 2 Stichproben
Die Ergebnisse, die in einem neuen Tabellenblatt erscheinen, zeigen, dass die H0-Hypothese abgelehnt werden muss, da der p-Wert 0,009 unterhalb unserer Grenze von 5 % liegt. Folglich können die Varianzen nicht als gleich angesehen werden. Die Länge der Blütenblätter der beiden Populationen - Versicolor und Setosa - folgt nicht derselben Verteilung.
Wir werden jetzt dasselbe tun, aber für die Breite der Blütenblätter.
Die einzige Änderung am oben beschriebenen Verfahren ist die Datenauswahl. Für Stichprobe 1 wählen Sie die Spalte C aus und für Stichprobe 2 wählen Sie die Spalte F aus.

Dieses Mal können die Varianzen als gleich angesehen werden, da der p-Wert des Tests (0,189) höher ist als 0,05.

Da die Gleichheit der Varianz oder Varianzhomogenität angenommen wird, können wir einen Test zum Vergleich der Mittelwerte durchführen.
Sie werden in der Tabelle mit deskriptiven Statistiken feststellen, dass der Mittelwert der Blütenblätter-Breite für Versicolor kleiner ist als der Mittelwert von Setosa für dasselbe Merkmal. Aus diesem Grund können wir einen einseitigen Test zum Testen des Mittelwerts durchführen.
Gehen Sie zum Menü Parametrische Tests/t-Test und z-Test für zwei Stichproben

In der Registerkarte Allgemein führen Sie die gleiche Stichprobenauswahl wie zuvor für die Blütenblätterbreite durch.
Wählen Sie die Option Student-Test, da wir die wahren Varianzen der Populationen nicht kennen.

In der Registerkarte Optionen wählen Sie die Alternative Mittelwert 1 – Mittelwert 2 < D, wobei D = 0.
Wir können für die Varianzen Gleichheit annehmen, da wir den Test gerade erst berechnet haben.

Klicken Sie auf OK.
Wie Sie an den Ergebnissen dieses Tests sehen können, schlussfolgern wir, dass eine signifikante Differenz zwischen den beiden Mittelwerten besteht, wobei die Blütenblätterbreite der Versicolor-Schwerlilie kleiner ist als die Blütenblätterbreite der Setosa-Schwertlilie. Die Breite der Blütenblätter der beiden Populationen - Versicolor und Setosa - folgt nicht derselben Verteilung.

War dieser Artikel nützlich?
- Ja
- Nein