Was ist statistische Modellierung?
Was ist statistische Modellierung?
Einfach ausgedrückt ist die statistische Modellierung eine vereinfachte mathematisch-formalisierte Methode, sich der Realität anzunähern (d. h. was Ihre Daten generieren) und optional auf der Grundlage dieser Annäherung Voraussagen zu treffen. Das statistische Modell ist die verwendete mathematische Gleichung.
Hier ein einfaches Beispiel. Angenommen, Sie möchten das Gewicht einer bestimmten Kartoffelsorte bestimmen. Hierfür gibt es eine schwierige und eine einfache Methode. Die schwierige Methode wäre, jahrelang jede einzelne Kartoffel dieser Sorte weltweit zu wiegen und die Daten in eine ellenlange Excel-Tabelle einzutragen. Die einfache Methode wäre, eine repräsentative Stichprobe von 30 Kartoffeln dieser Sorte auszuwählen, den Mittelwert und die Standardabweichung zu berechnen und nur diese beiden Zahlen als näherungsweise Beschreibung des Gewichts einzutragen. Die Darstellung einer Menge anhand eines Mittelwerts und einer Standardabweichung ist eine sehr einfache Form der statistischen Modellierung.
Ein weiteres Beispiel ist der Versuch, die Höhe von Pflanzen entsprechend dem Wassergehalt des Bodens nach Durchführung eines Experiments mit einer Stichprobe von Pflanzen, die einer steigenden Bodenfeuchtigkeit ausgesetzt sind, durch eine Gerade mit entsprechender Steigung und entsprechendem Schnittpunkt darzustellen. Dieses besondere Modell wird als einfache lineare Regression bezeichnet.

Was sind abhängige und erklärende Variablen?
In fast allen Fällen beinhalten statistische Modelle erklärende und abhängige Variablen. Die abhängige Variable ist die Variable, die wir beschreiben, erklären und vorhersagen möchten. Als Faustregel gilt, dass die abhängige Variable oft die Variable ist, die wir in Modellierungsdiagrammen auf der Y-Achse verwenden. Beim Beispiel der Pflanzenhöhe ist die abhängige Variable die Pflanzenhöhe. Erklärende Variablen, die auch als unabhängige Variablen bezeichnet werden, sind die Variablen, die wir verwenden, um die abhängigen Variablen zu erklären, zu beschreiben oder vorherzusagen. Erklärende Variablen werden oft auf der X-Achse dargestellt. Das Beispiel der Pflanzenhöhe umfasst nur eine erklärende Variable, die quantitativ ist: der Wassergehalt des Bodens. Sowohl abhängige als auch erklärende Variablen können einzeln oder multipel, quantitativ oder qualitativ sein. Es gibt an verschiedene Situationen angepasste Modelle.
Was ist ein Modellparameter?
In klassischen, parametrischen Modellen ist/sind die abhängige(n) Variable(n) mit den erklärenden Variablen über eine mathematische Gleichung (das Modell) verknüpft, die als Modellparameter bezeichnete Mengen beinhaltet. Im einfachen linearen Regressionsbeispiel der Pflanzenhöhe sind die Parameter der Schnittpunkt und die Steigung1. Die Gleichung könnte folgendermaßen lauten: Höhe = Schnittpunkt + Steigung*Wassergehalt des Bodens Berechnungen hinter der statistischen Modellierung ermöglichen die Schätzung von Modellparametern und weitere Voraussagen zur abhängigen Variable. 1Die einfache lineare Regression beinhaltet einen dritten Parameter, die Varianz der Residuen (siehe nachstehender Abschnitt).
Was ist ein Modellresiduum?
Technisch gesehen sind Modellresiduen (oder Fehler) die Entfernungen zwischen Datenpunkten und dem Modell (was beim linearen Regressionsbeispiel der Pflanzenhöhe durch die Gerade dargestellt wird).

Modellresiduen stellen den Anteil der Variabilität der Daten dar, den das Modell nicht erfassen konnte. Das Bestimmtheitsmaß R² ist der durch das Modell erklärte Anteil der Variabilität. Je geringer die Residuen, desto höher das Bestimmtheitsmaß R².
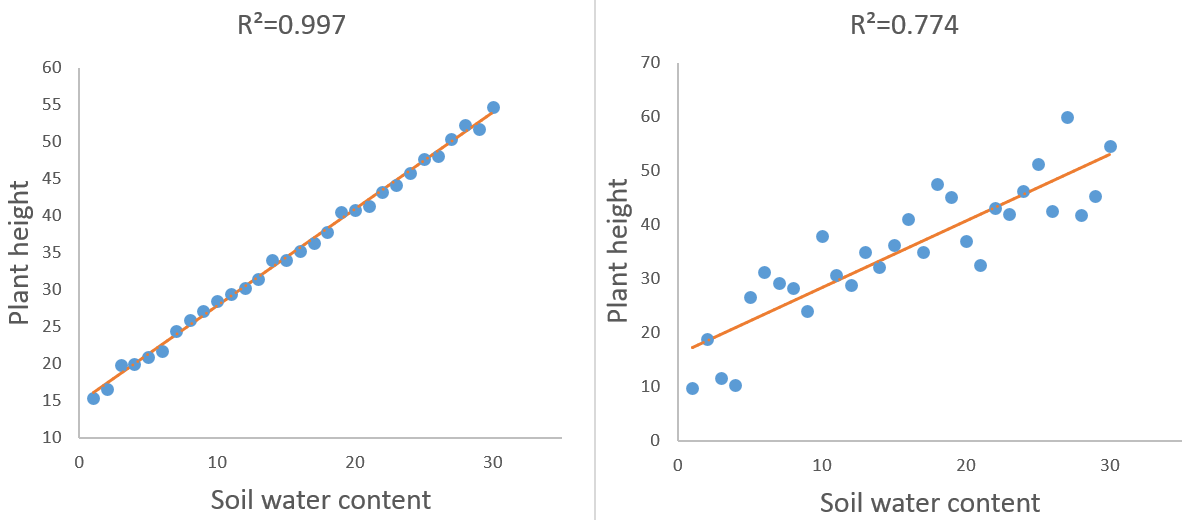
Wahl des geeigneten Residuen-Modells
Dieses Raster hilft Ihnen, aus den je nach Art und Anzahl der abhängigen und unabhängigen Variablen am häufigsten verwendeten Modelle das passende Modell auszuwählen. Neben parametrischen Modellen werden auch andere Lösungen vorgeschlagen.
War dieser Artikel nützlich?
- Ja
- Nein